In the previous article, we have solved long answer type questions of Parabola Chapter . In this article, we have solved Short answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Find the axis, co-ordinates of vertex and focus, length of latus rectum , equation of
Find the axis, co-ordinates of vertex and focus, length of latus rectum , equation of
directrix and the co-ordinates of the ends of latus rectum for each of the following parabolas :
![]()
Solution.

![]()
So, the focus ![]()
Axis of the parabola ![]() positive
positive ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix ![]()
The extremities of latus rectum :
![]()
![]()
Solution.

![]()
So, the focus ![]()
Axis of the parabola ![]() negative
negative ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix ![]()
The extremities of latus rectum :
![]()
![]()
Solution.

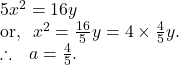
So, the focus ![]()
Axis of the parabola ![]() positive
positive ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix

The extremities of latus rectum :
![]()
![]()
Solution.

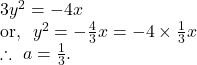
So, the focus ![]()
Axis of the parabola ![]() negative
negative ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix
![]()
The extremities of latus rectum :
![]()
![]()
Solution.

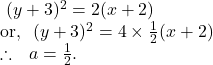
So, the focus ![]()
Axis of the parabola ![]() parallel to
parallel to ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix
![]()
The extremities of latus rectum :
![]()
![]()
Solution.


So, the focus ![]()
![]()
Axis of the parabola ![]() parallel to
parallel to ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix
![]()
The extremities of latus rectum :
![]()
![]()
Solution.
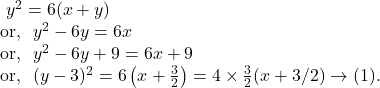
Comparing the parabola ![]() with the general equation of parabola
with the general equation of parabola ![]() , we get
, we get
So, the focus ![]()
Axis of the parabola ![]() parallel to
parallel to ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix :
![]()
![]()
Solution.
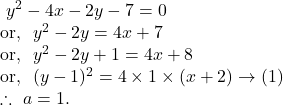
Comparing the parabola ![]() with the general equation of parabola
with the general equation of parabola ![]() , we get
, we get
So, the focus ![]()
![]()
Axis of the parabola ![]() parallel to
parallel to ![]() axis.
axis.
Vertex ![]()
Length of the latus rectum ![]()
The equation of the directrix :
![]()