
1. Reduce the equation of the plane ![]() to the intercept form and find its intercepts on the coordinate axes.
to the intercept form and find its intercepts on the coordinate axes.
Solution.
The given equation can be written as
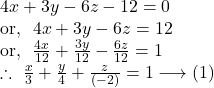
So, the equation (1) represents the intercept form of the plane and the lengths of the intercepts from ![]() axis,
axis, ![]() axis and
axis and ![]() axis are given by
axis are given by ![]() and
and ![]()
2. Find the normal vector to the plane ![]() Also, find a unit vector normal to the plane
Also, find a unit vector normal to the plane
Solution.
The normal vector to the plane ![]() is given by
is given by ![]()
So, the unit vector normal to the plane is
![]()
3. Find the vector equation of the following planes in scalar product form ![]()
![]()
Solution.
We know that the equation ![]() represents a plane passing through a point having position vector
represents a plane passing through a point having position vector ![]() and parallel to vectors
and parallel to vectors ![]() and
and ![]() [where
[where ![]() and
and ![]() are scalars]. Here,
are scalars]. Here, ![]() and
and ![]()
The given plane is perpendicular to the vector

So, the vector equation of the plane in scalar product form is
![]()
Hence, the required vector equation is given by ![]()
![]()
Solution.
![]()
The given plane is perpendicular to the vector
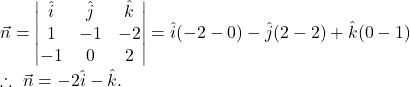
So, the general form ![]() of the plane is given by
of the plane is given by
![]()
![]()
Solution.

So, the general form ![]() of the plane is given by
of the plane is given by
![]()
4. Find the cartesian form of the equation of the following planes :
![]()
Solution.

So, the general form ![]() of the plane is given by
of the plane is given by

So, the cartesian form of the equation of the plane is given by
![]()
![]()
Solution.
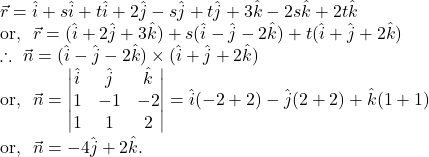
So, the general form ![]() of the plane is given by
of the plane is given by

Hence, the cartesian form of the plane is given by
![]()