Integration By Parts (Part-3)| S N Dey| Class 12

by

In the previous article, we have discussed the solutions of VSA type questions of Integration By Parts Chapter of S N Dey mathematics Class 12. In this chapter, we will discuss the problems of Short Answer Type Questions.

Integration By Parts
Integration By Parts | Short Answer type Questions’ Solution

11.~~\displaystyle\int{x^3\sin x}~dx

Solution.

\displaystyle\int{x^3\sin x}~dx\\=x^3\int{\sin x}-\int{\left[\frac{d}{dx}(x^3)\int{\sin x}~dx\right]}~dx\\=x^3(-\cos x)-\int{3x^2(-\cos x)}~dx\\=-x^3\cos x+3\int{x^2\cos x}~dx\\=-x^3\cos x+3I_1 \rightarrow(1)

~I_1\\=\displaystyle\int{x^2\cos x}~dx\\=x^2\int{\cos x}~dx-\int{\left[\frac{d}{dx}(x^2)\int{\cos x}~dx\right]}~dx\\=x^2\sin x-\int{2x\sin x~dx}\\=x^2\sin x-2\int{x\sin x~dx}\\=x^2\sin x-2I_2\rightarrow(2)

I_2\\=\displaystyle\int{x\sin x~dx}\\=x\int{\sin x~dx}-\int{\left[\frac{d}{dx}(x)\int{\sin x}~dx\right]}~dx\\=-x\cos x+\int{1 \cdot \cos x~dx}\\=-x\cos x+\sin x\rightarrow(3)

So, by ~(1),~(2),~(3)~ we get,

~\displaystyle\int{x^3\sin x}~dx\\=-x^3\cos x+3(x^2\sin x-2I_2)\\=-x^3\cos x+3x^2\sin x-6(-x\cos x+\sin x)\\=3(x^2-2)\sin x-x(x^2-6)\cos x+c.

12.~~\displaystyle\int{\sin^{-1}(\sqrt{x})}~dx

Solution.

\displaystyle\int{\sin^{-1}(\sqrt{x})}~dx \rightarrow(1)

\text{let}~~ ~\sin^{-1}(\sqrt{x})=\theta \\ \therefore \sqrt{x}=\sin\theta \\ \text{or,}~~ x=\sin^2\theta \\ \therefore ~dx=2\sin\theta\cos\theta~d\theta=\sin2\theta~d\theta.

From ~(1),~ we get,

~\displaystyle\int{\sin^{-1}(\sqrt{x})}~dx\\=\int{\theta \sin2\theta~d\theta} \\=\theta\int{\sin2\theta~d\theta}-\int{\left[\frac{d}{d\theta}(\theta)\int{\sin2\theta}~d\theta\right]}~d\theta\\=\theta(-\frac 12\cos2\theta)-\int{(-\frac 12\cos2\theta)~d\theta}\\=-\frac 12\theta~\cos2\theta+\frac 12\int{\cos2\theta~d\theta}\\=-\frac 12\theta\cos2\theta+\frac 12 \times \frac 12(\sin2\theta)+c\\=-\frac 12\theta(1-2\sin^2\theta)+\frac 14 \times 2\sin\theta\cos\theta+c\\=\frac 12 \theta(2\sin^2\theta-1)+\frac 12\sin\theta(\sqrt{1-\sin^2\theta})+c\\=\frac 12(2x-1)\sin^{-1}(\sqrt{x})+\frac 12\sqrt{x}\sqrt{1-x}+c.

13.~~\displaystyle\int{\log(1+x)^{1+x}}~dx

Solution.

\displaystyle\int{\log(1+x)^{1+x}}~dx\\=\int{(1+x)\log(1+x)}~dx\\=\log(1+x) \int{(1+x)~dx}\\=\log(1+x)~\times \left(x+\frac {x^2}{2}\right)-\int{\left[\frac{d}{dx}\log(1+x)~\int{(1+x)~dx}\right]}~dx\\=\log(1+x)~\times \left(x+\frac {x^2}{2}\right)-\int{\frac{1}{1+x} \times \left(x+\frac {x^2}{2}\right)}~dx\\=\log(1+x)~\times \left(x+\frac {x^2}{2}\right)-\int{\frac{x}{1+x}}~dx-\frac 12\int{\frac{x^2}{1+x}}~dx\\=\log(1+x)~\times \left(x+\frac {x^2}{2}\right)-\int{\left(1-\frac{1}{1+x}\right)~dx}-\frac 12\int{\frac{x^2-1+1}{x+1}}~dx\\=\log(1+x)~\times \left(x+\frac {x^2}{2}\right)-x+\log(1+x)-\frac 12\int{(x-1)}~dx-\frac 12\int{\frac{1}{1+x}}~dx\\=\log(1+x)~\times \left(x+\frac {x^2}{2}\right)-x+\frac 12\log(1+x)-\frac 12\left(\frac{x^2}{2}-x\right)-\frac 12\log(1+x)\\=\log(1+x)~\times \left(x+\frac {x^2}{2}+1-\frac 12\right)-x+\frac x2-\frac{x^2}{4}+c\\=\frac 12(1+x)^2~\log(1+x)-\frac{1}{4}x(x+2)+c.

14.~~\displaystyle \int{\tan^{-1}~\frac{2x}{1-x^2}}~dx~~(-1<x<1)

Solution.

We know ~~\tan^{-1}~\frac{2x}{1-x^2}=2\tan^{-1}x

\displaystyle\int{\tan^{-1}~\frac{2x}{1-x^2}}~dx\\=2\int{\tan^{-1}x}~dx\\=2I_1\rightarrow(1)

I_1\\=\displaystyle\int{\tan^{-1}x}~dx\\=\tan^{-1}x \int{dx}-\int{\left[\frac{d}{dx}(\tan^{-1}x)\int{dx}\right]}~dx\\=\tan^{-1}x \cdot x-\int{\frac{1}{1+x^2} \cdot x}~dx\\=x\tan^{-1}x-\frac 12\int{\frac{2x}{1+x^2}}~dx\\=x\tan^{-1}x-\frac 12\int{\frac{d(1+x^2)}{1+x^2}}\\=x\tan^{-1}x-\frac 12\log|1+x^2|+c_1\rightarrow(2)

From ~(1),~(2)~ we get,

\displaystyle\int{\tan^{-1}~\frac{2x}{1-x^2}}~dx\\=2\left(x\tan^{-1}x-\frac 12\log|1+x^2|+c_1 \right)\\=2x\tan^{-1}x-\log|1+x^2|+c.~~[~c=2c_1]

15.~~\displaystyle\int{\cos^{-1}~\frac{1-x^2}{1+x^2}}~dx

Solution.

We know, ~~\cos^{-1}~\frac{1-x^2}{1+x^2}=2\tan^{-1}x

~\displaystyle\int{\cos^{-1}~\frac{1-x^2}{1+x^2}}~dx=2\int{\tan^{-1}x}~dx \rightarrow(1)

~\displaystyle\int{\tan^{-1}x}~dx \\=\tan^{-1}x\int{dx}-\int{\left[\frac{d}{dx}(\tan^{-1}x) \int{dx}\right]}~dx\\=x\tan^{-1}x-\int{\frac{1}{1+x^2} \cdot x}~dx\\=x\tan^{-1}x-\frac 12\int{\frac{2x}{1+x^2}}~dx\\=x\tan^{-1}x-\frac 12\int{\frac{d(1+x^2)}{1+x^2}}\\=x\tan^{-1}x-\frac 12\log|1+x^2|+c_1 \rightarrow(2)

From ~(1),~(2)~ we get,

~\displaystyle\int{\cos^{-1}~\frac{1-x^2}{1+x^2}}~dx\\=2x\tan^{-1}x-\log|1+x^2|+c.~~[~c=2c_1~]

16.~~\displaystyle\int{\log(\sin x)\cdot \cos x}~dx

Solution.

\displaystyle\int{\log(\sin x)\cdot \cos x}~dx\rightarrow(1)

~\text{let}~\sin x=z \Rightarrow \cos x~dx=dz\rightarrow(2)

By ~(1),~(2)~ we get,

\displaystyle\int{\log(\sin x)\cdot \cos x}~dx\\=\int{\log z}~dz\\=\log z\int{dz}-\int{\left[\frac{d}{dz}(\log z)\int{dz}\right]}~dz\\=z\log z-\int{\frac 1z \times z~dz}\\=z\log z-\int{dz}\\=z\log z-z+c\\=z(\log z-1)+c\\=\sin x[\log(\sin x)-1]+c.

17.~~ \displaystyle\int{\frac{x\sin^{-1}x}{\sqrt{1-x^2}}~dx}

Solution.

~\text{let}~\sin^{-1}x=z \Rightarrow \frac{1}{\sqrt{1-x^2}}~dx=dz.

\displaystyle\int{\frac{x\sin^{-1}x}{\sqrt{1-x^2}}~dx}\\=\int{z\sin z}~dz\\ [ ~\because ~\sin^{-1}x=z \Rightarrow x=\sin z]\\=z\int{\sin z~dz}-\int{\left[\frac{d}{dz}(z)\int{\sin z~dz}\right]}~dz\\=z(-\cos z)-\int{1 \cdot(-\cos z)}~dz\\=-z\cos z+\int{\cos z~dz}\\=-z\cos z+\sin z+c\\=-z\sqrt{1-\sin^2z}+\sin z+c\\=-\sin^{-1}x \cdot \sqrt{1-x^2}+x+c\\=x-\sqrt{1-x^2}\sin^{-1} x+c.

18.~~\displaystyle\int{e^{x^3}x^5}~dx

Solution.

\displaystyle\int{e^{x^3}x^5}~dx\\=\frac13\displaystyle\int{e^{x^3} \cdot x^3\cdot3x^2}~dx\\=\frac 13\int{e^z \cdot z}~dz ~~[~z=x^3 \Rightarrow~ dz=3x^2~dx~]\\=\frac 13I_1\rightarrow(1)

I_1\\=\displaystyle\int{e^z \cdot z}~dz\\=z\int{e^z~dz}-\int{\left[\frac{d}{dx}(z)\int{e^z~dz}\right]}~dz\\=ze^z-\int{1 \cdot e^z~dz}\=ze^z-e^z\\=e^z(z-1)\rightarrow(2)

Hence, from ~(1),~(2)~ we get,

\displaystyle\int{e^{x^3}x^5}~dx\\=\frac 13e^{x^3}(x^3-1)+c.

19.~~\displaystyle\int{\frac{x}{1+\cos2x}}~dx

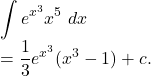
Solution.

\displaystyle\int{\frac{x}{1+\cos2x}}~dx\\=\int{\frac{x}{2\cos^2x}}~dx\\=\frac 12 \int{x\sec^2x}~dx\\=\frac 12I_1\rightarrow(1)

I_1\\=\displaystyle\int{x\sec^2x}~dx\\=x\int{\sec^2x}~dx-\int{\left[\frac{d}{dx}(x)\int{\sec^2x}~dx\right]}~dx\\=x\tan x-\int{1\cdot \tan x}~dx\\=x\tan x-\log|\sec x|+c_1\\=x\tan x+\log|\cos x|+c_1\rightarrow(2)

Hence, from ~(1),~(2)~ we get,

\displaystyle\int{\frac{x}{1+\cos2x}}~dx\\=\frac 12(x\tan x+\log|\cos x|+c_1)\\=\frac 12(x\tan x+\log|\cos x|)+c~~\left[~\frac 12c_1=c~\right]

20.~~\displaystyle\int{x\sin x\cos x}~dx

Solution.

\displaystyle\int{x\sin x\cos x}~dx\\=\frac 12\int{x(2\sin x\cos x)}~dx\\=\frac 12\int{x\sin 2x}~dx\\=\frac 12I_1 \rightarrow(1)

I_1\\=\displaystyle\int{x\sin 2x}~dx\\=x\int{\sin 2x}~dx-\int{\left[\frac{d}{dx}(x)\int{\sin2x}~dx\right]}~dx\\=x \cdot (-\frac 12 \cos2x)-\int{\left[1 \cdot (-\frac 12 \cos2x)\right]}~dx\\=-\frac x2\cos2x+\frac 12\int{\cos2x}~dx\\=-\frac x2\cos 2x+\frac 14\sin2x+c_1\rightarrow(2)

Hence, from ~(1),~(2)~ we get,

\displaystyle\int{x\sin x\cos x}~dx\\=\frac 12(-\frac x2\cos 2x+\frac 14\sin2x+c_1)\\=-\frac x4\cos2x+\frac 18\sin2x+c.~~\left[~c=\frac 12c_1~\right]

Post Views: 99

Leave a Comment