In the previous article, we have solved few Short answer type questions (5-10) of Parabola Chapter . In this article, we have solved Short answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Show that the locus of the middle points of chords of the parabola
Show that the locus of the middle points of chords of the parabola ![]() passing through the vertex is the parabola
passing through the vertex is the parabola ![]()
Solution.

One end of the chord is the vertex of parabola, which is ![]() .
.
Let the mid point of the chords be ![]() and the other end of the chord be
and the other end of the chord be ![]()
Mid-point of ![]() is
is ![]()
![]()
![Rendered by QuickLaTeX.com \text{So,}~h=at\rightarrow(1),~~\\ k=\frac 12 at^2=\frac 12 a(h/a)^2~~[\text{By (1)}] \\ \text{or,}~~ k=\frac{h^2}{2a} \Rightarrow h^2=2ka \rightarrow(2).](https://examhoop.com/wp-content/ql-cache/quicklatex.com-90493ef4441205a79d5ceb71ba4d5208_l3.png)
![]() Find the locus of the middle points of a family of focal chords of the parabola
Find the locus of the middle points of a family of focal chords of the parabola ![]()
Solution.
The extremities of the focal chord of the parabola ![]() are
are ![]() and
and ![]()
Let the mid-point of the chord be ![]()
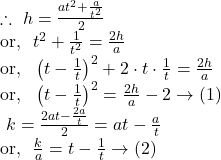
From ![]() and
and ![]() we get,
we get,

Hence, the locus of the mid-point ![]() of the chord is
of the chord is
![]()
![]() is any ordinate of the parabola
is any ordinate of the parabola ![]() the point
the point ![]() divides
divides ![]() in the ratio
in the ratio ![]() Find the locus of
Find the locus of ![]()
Solution.

Let ![]() be any point on the parabola and
be any point on the parabola and ![]() be the ordinate of the parabola.
be the ordinate of the parabola.
![]()
Again, let ![]() divides
divides ![]() in the ratio
in the ratio ![]()

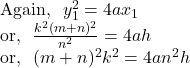
![]() the locus of the point
the locus of the point ![]() is
is ![]()
![]() Prove that the lines joining the ends of latus rectum of the parabola
Prove that the lines joining the ends of latus rectum of the parabola ![]() with the point of intersection of its axis and directrix are at right angles.
with the point of intersection of its axis and directrix are at right angles.
Solution.
Let ![]() be the focus and
be the focus and ![]() be the length of the latus rectum of length
be the length of the latus rectum of length ![]() unit of the parabola
unit of the parabola ![]()
![]()

The directrix of the parabola ![]() and the axis of the parabola
and the axis of the parabola ![]()
So, the point of intersection of the directrix and the axis of the parabola is ![]()
Slope ![]() of
of ![]() is
is ![]()
Slope ![]() of
of ![]() is
is ![]()
So, ![]()
Hence, ![]()
![]() Prove that the lines joining the ends of latus rectum of the parabola
Prove that the lines joining the ends of latus rectum of the parabola ![]() The ordinate of
The ordinate of ![]() is twice that of
is twice that of ![]() Prove that the locus of the mid-point of
Prove that the locus of the mid-point of ![]() is
is ![]()
Solution.
Let ![]()

By question, ![]()
Now, since ![]() lies on the parabola ,
lies on the parabola ,
![]()
Let ![]() be the mid-point of
be the mid-point of ![]()
![]()
![]()
By ![]() , we get
, we get
![Rendered by QuickLaTeX.com ~y_1^2+y_2^2=4a(x_1+x_2) \\ \text{or,}~~ y_1^2+4y_1^2=4a(x_1+x_2)\\ \text{or,}~~ 5(2k/3)^2=4a \times 2h~~[\text{By (4),~(5)}] \\ \text{or,}~~ 5k^2=18ah.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-3f78dafcf4c7ad63fd89dc52346defdd_l3.png)
Hence, the locus of ![]() is
is ![]()