In the previous article, we have solved few Short answer type questions of Parabola Chapter . In this article, we have solved Short answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Find the equation of the parabola whose focus is at the origin and the equation of the directrix is
Find the equation of the parabola whose focus is at the origin and the equation of the directrix is ![]()
Solution.
Focus ![]() Directrix
Directrix ![]()
Let ![]() be any point on the parabola.
be any point on the parabola.

Also, ![]()
For parabola,
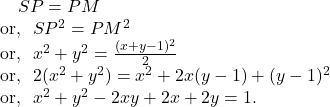
![]() Find the equation of the parabola whose focus is
Find the equation of the parabola whose focus is ![]() and whose directrix is
and whose directrix is ![]()
Solution.
Focus : ![]() Directrix :
Directrix : ![]()
Let ![]() be any point on the parabola.
be any point on the parabola.
We know,
Distance between ![]() and
and ![]() Perpendicular distance to directrix from
Perpendicular distance to directrix from ![]()
![]() The equation of the directrix of a parabola is
The equation of the directrix of a parabola is ![]() and the co-ordinates of its focus are
and the co-ordinates of its focus are ![]() . Find the equation of the parabola.
. Find the equation of the parabola.
Focus : ![]() Directrix :
Directrix : ![]()
Let ![]() be any point on the parabola.
be any point on the parabola.
We know,
Distance between ![]() and
and ![]() Perpendicular distance to directrix from
Perpendicular distance to directrix from ![]()

![]() Find the co-ordinates of vertex and the length of latus rectum of the parabola whose focus is
Find the co-ordinates of vertex and the length of latus rectum of the parabola whose focus is ![]() and the directrix is the line
and the directrix is the line ![]()
Solution.
We know that the directrix ![]() axis of the parabola.
axis of the parabola.
Now, the slope of the directrix ![]()
So, the slope of the axis ![]()
Equation of the axis which passes through the point ![]() and having slope
and having slope ![]() is
is ![]()
Let ![]() be the point of intersection of the straight lines
be the point of intersection of the straight lines ![]() and
and ![]()
Solving ![]() and
and ![]() we get
we get ![]()
![]()
Since vertex![]() is the mid-point of
is the mid-point of ![]() and
and ![]()
![]()

Hence, the length of the latus rectum ![]()
![]() A point moves in such a way that its distance from the point
A point moves in such a way that its distance from the point ![]() is equal to its distance from the line
is equal to its distance from the line ![]() Find the equation of its path. What is the name of the curve ?
Find the equation of its path. What is the name of the curve ?
Solution.
Let at any instant the co-ordinates of the moving point ![]() be
be ![]()
The distance between the point ![]() and
and ![]() is
is
![]()
Again, the distance of the point ![]() from the from the line
from the from the line ![]() is
is
![]()
By question,
![Rendered by QuickLaTeX.com ~ \sqrt{(h-2)^2+(k-5)^2}=\frac{|2h+4k-3|}{\sqrt{20}} \\ \text{or,}~~ (h-2)^2+(k-5)^2=\frac{(2h+4k-3)^2}{20} \\ \text{or,}~~ (2h+4k-3)^2=20[(h-2)^2+(k-5)^2]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-ede3ddfc302ee8bba82637cf12e81a02_l3.png)
Hence, the locus of the point ![]() is
is
![]() .
.
We know that if a point moves in such a way that it is always equidistant from a fixed point and from a fixed straight line, then the locus of the point will be parabola. So, the name of the curve is parabola.
![]() The co-ordinates of a moving point
The co-ordinates of a moving point ![]() are
are ![]() ; show that the locus of
; show that the locus of ![]() is a parabola.
is a parabola.
Solution.
![]()
From ![]() and
and ![]() we get
we get

Hence, by ![]() we can say that the locus of the given point is a parabola.
we can say that the locus of the given point is a parabola.
![]() If
If ![]() is a variable parameter, show that the equations
is a variable parameter, show that the equations ![]() represent the equation of a parabola. Find the co-ordinates of vertex, focus and the length of latus rectum of the parabola.
represent the equation of a parabola. Find the co-ordinates of vertex, focus and the length of latus rectum of the parabola.
Solution.

We know that
![Rendered by QuickLaTeX.com ~1+\cot^2\theta=\csc^2\theta \\ \text{or,}~~ 1+(y-2)^2=3-4x ~~[\text{By (1),(2)}] \\ \text{or,}~~ (y-2)^2=2-4x \\ \text{or,}~~ (y-2)^2=-4\left(x-\frac 12 \right) \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-755d32618909c4df888289178217d40d_l3.png)
Hence, by ![]() we can conclude that the given equations represent a parabola.
we can conclude that the given equations represent a parabola.
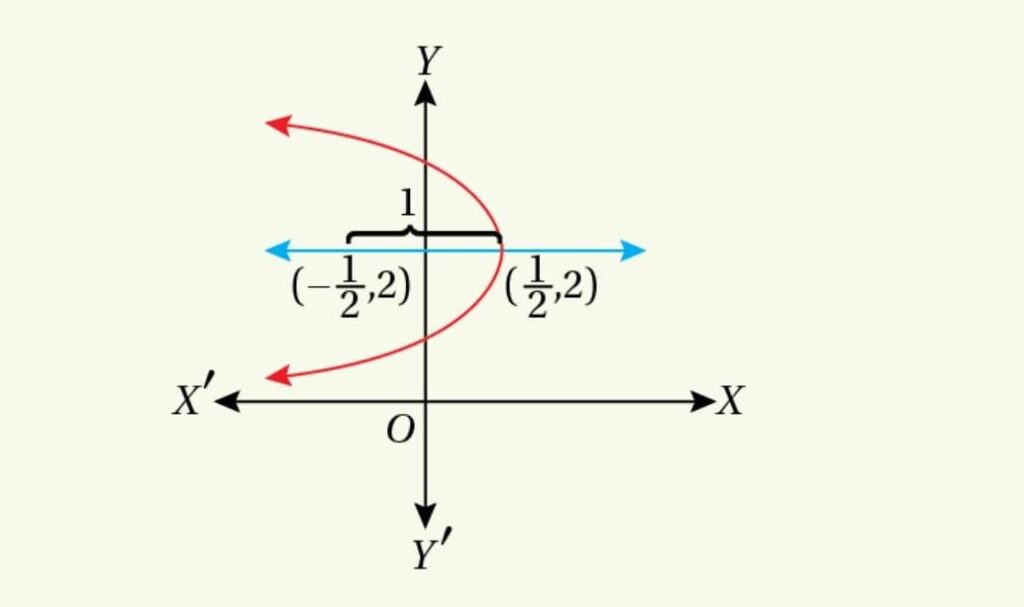
Here, ![]()
Vertex ![]()
Focus ![]()
Length of the latus rectum ![]()
![]() Find the equation of the circle, one of whose diameters is the latus rectum of
Find the equation of the circle, one of whose diameters is the latus rectum of ![]() Show that this circle goes through the common point of the axis and the directrix of the parabola.
Show that this circle goes through the common point of the axis and the directrix of the parabola.
Solution.
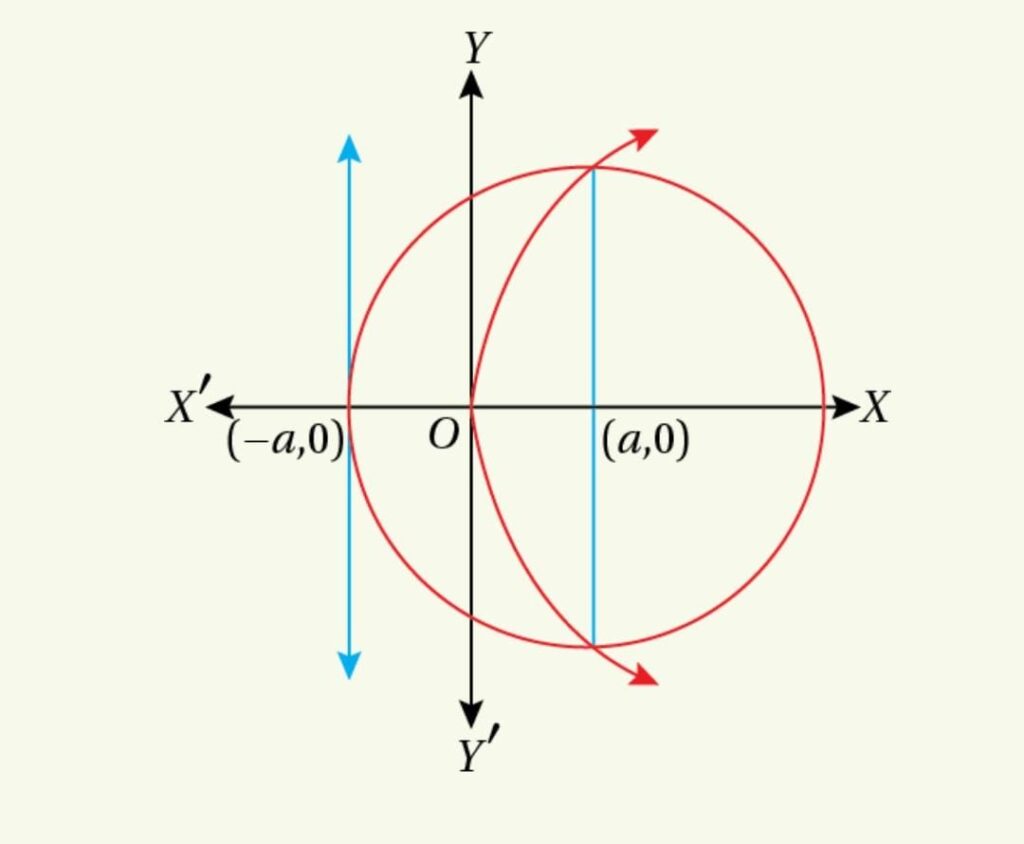
For the parabola ![]() the length of the latus rectum is
the length of the latus rectum is ![]() unit and the focus is
unit and the focus is ![]()
Since the diameter of the circle is the latus rectum of the parabola, so the centre of the circle is the mid-point of the latus rectum which is ![]()
Now, the equation of the circle having centre ![]() and with diameter
and with diameter ![]() is given by
is given by
![]()
So, the intersection of the axis and the directrix is ![]()
Now putting ![]() in the left hand side of
in the left hand side of ![]() we get
we get
![]()
So, the circle ![]() passes through the point
passes through the point ![]()
Hence, we can conclude that this circle goes through the common point of the axis and the directrix of the parabola.