In the previous article , we solved few solutions of Long Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.

8. ![]() is any double ordinate of the ellipse
is any double ordinate of the ellipse ![]() ; find the equation to the locus of the point of trisection of
; find the equation to the locus of the point of trisection of ![]() that is nearer to
that is nearer to ![]()
Solution.
Let ![]()
Suppose that the point ![]() is the nearest point of
is the nearest point of ![]() which is the point of trisection of
which is the point of trisection of ![]() i.e.,
i.e., ![]()
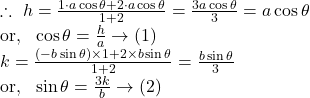
![Rendered by QuickLaTeX.com \because~ \sin^2\theta+\cos^2\theta=1 \\ \text{or,}~~ \left(\frac{3k}{b}\right)^2+\left(\frac ha\right)^2=1~~[\text{By (1),(2)}] \\ \text{or,}~~ \frac{9k^2}{b^2}+\frac{h^2}{a^2}=1 \\ \text{or,}~~ \frac{h^2}{a^2}+\frac{9k^2}{b^2}=1\rightarrow(3)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-6564acd1b68ea8fb9858915958027965_l3.png)
Hence, from ![]() we get the locus of the point which is
we get the locus of the point which is ![]()
For Full Solution PDF of the Ellipse (S N De-Chhaya Mathematics), click here.
9. Show that the double ordinate of the auxiliary circle of an ellipse passing through the focus is equal to the minor axis of the ellipse.
Solution.

Let the equation of the ellipse be
![]()
and the auxiliary circle of ![]() is
is ![]()
Suppose that ![]() is the double ordinate of the auxiliary circle
is the double ordinate of the auxiliary circle ![]()
![]()
Now, the equation of ![]() is given by
is given by ![]()
Since ![]() passes through the focus i.e.,
passes through the focus i.e., ![]() , so
, so
![]()
Since the auxiliary circle has double ordinate,
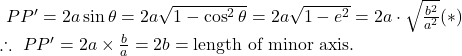
Note[*] : ![]()
10. ![]() is the centre of an ellipse whose semi-minor axis is
is the centre of an ellipse whose semi-minor axis is ![]() The ordinate of a point
The ordinate of a point ![]() of the ellipse intersects its auxiliary circle at
of the ellipse intersects its auxiliary circle at ![]() (when produced). The straight line through
(when produced). The straight line through ![]() drawn parallel to
drawn parallel to ![]() cuts the major axis at
cuts the major axis at ![]() Prove that,
Prove that, ![]()
Solution.
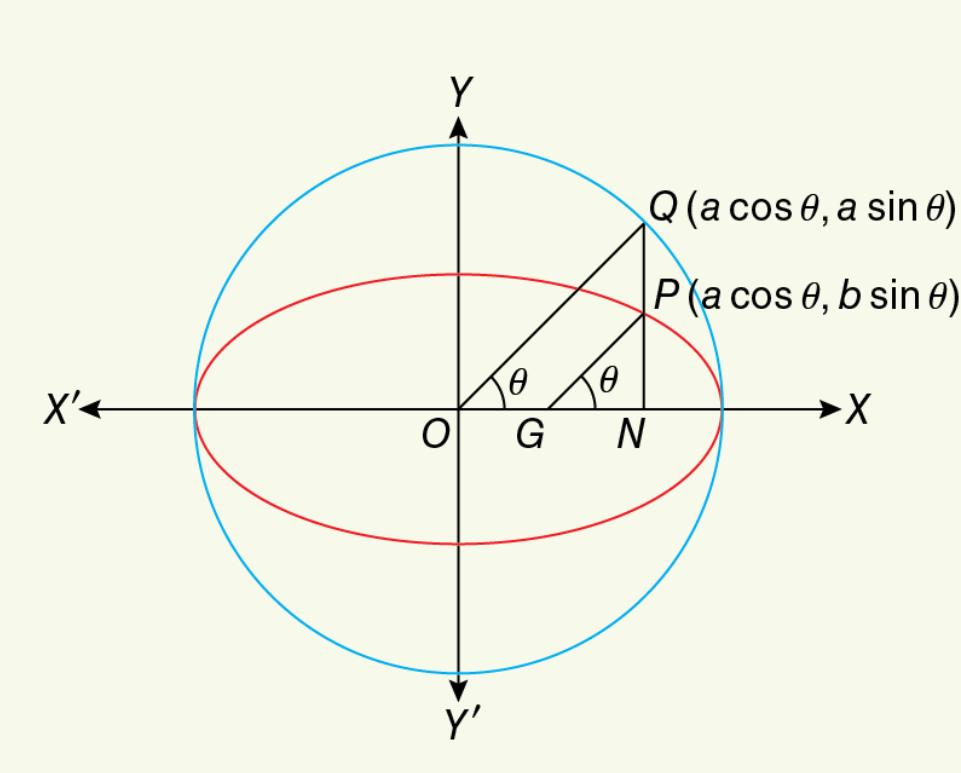
Let the equation of the ellipse be ![]()
Clearly,![]() and
and ![]() are similar triangle,
are similar triangle,
11. If ![]() and
and ![]() are the eccentric angles of the points
are the eccentric angles of the points ![]() and
and ![]() respectively on the ellipse
respectively on the ellipse ![]() , show that the equation of the chord
, show that the equation of the chord ![]() is
is
![]()
Solution.
Since ![]() are the eccentric angles of the points
are the eccentric angles of the points ![]() and
and ![]() respectively, so
respectively, so
![]()
![]() The equation of
The equation of ![]() is
is
![Rendered by QuickLaTeX.com ~\frac{y-a\sin(\alpha+\beta)}{x-a\cos(\alpha+\beta)}=\frac{b\sin(\alpha-\beta)-b\sin(\alpha+\beta)}{a\cos(\alpha-\beta)-a\cos(\alpha+\beta)} \\ \text{or,}~~ \frac{y-b\sin(\alpha+\beta)}{x-a\cos(\alpha+\beta)}=\frac ba \cdot \frac{-2\cos\alpha \sin\beta}{2\sin\alpha \sin\beta} \\ \text{or,}~~ \frac{y-b\sin(\alpha+\beta)}{x-a\cos(\alpha+\beta)}=-\frac ba \cdot \frac{\cos\alpha}{\sin\alpha} \\ \text{or,}~~ bx \cos\alpha+ay\sin\alpha=ab[\cos(\alpha+\beta)\cos\alpha+\sin(\alpha+\beta)\sin\alpha] \\ \text{or,}~~ bx\cos\alpha+ay\sin\alpha=ab\cos\beta \\ \therefore~ \frac xa \cos\alpha+\frac yb \sin\alpha=\cos\beta.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-a733a4094ed8e2cce5acc1e9b810ae6d_l3.png)
Read More :