In the previous article , we solved few solutions of Long Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.

![]() The ellipse
The ellipse ![]() passes through
passes through ![]() and its eccentricity is
and its eccentricity is ![]() find the length of its latus rectum.
find the length of its latus rectum.
Solution.
Since the given ellipse ![]() passes through the point
passes through the point ![]() , so
, so
![]()
Again, the eccentricity ![]() of the ellipse is
of the ellipse is
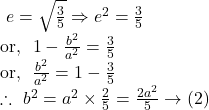
So, from ![]() and
and ![]() we get,
we get,

From ![]() we get,
we get, ![]()
So, the length of the latus rectum is
![]()
![]() The ellipse
The ellipse ![]() passes through the point of intersection of the lines
passes through the point of intersection of the lines ![]() and
and ![]() and its length of latus rectum is
and its length of latus rectum is ![]() find
find ![]() and
and ![]()
Solution.
Two given straight lines are ![]() and
and ![]()
From ![]() and
and ![]() we get,
we get,
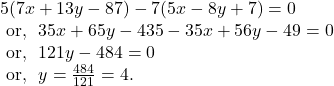
From ![]() we get,
we get,

So, the given ellipse ![]() passes through the point
passes through the point ![]()
![]()
So, the length of latus rectum is
![]()
From ![]() and
and ![]() we get,
we get,
![Rendered by QuickLaTeX.com \frac{25}{a^2}+\frac{16}{\frac{16\sqrt{2}}{5}a}=1 \\ \text{or,}~~ \frac{25}{a^2}+\frac{5}{\sqrt{2}a}=1 \\ \text{or,}~~ 25\sqrt{2}+5a=\sqrt{2}a^2 \\ \text{or,}~~ \sqrt{2}a^2-5a-25\sqrt{2}=0 \\ \therefore~ a=\frac{5 \pm \sqrt{(-5)^2-4\sqrt{2}(-25\sqrt{2})}}{2\sqrt{2}}=\frac{5 \pm \sqrt{25+100\times 2}}{2\sqrt{2}} \\ \text{or,}~~ a=\frac{5 \pm\sqrt{225}}{2\sqrt{2}}=\frac{5 \pm 15}{2\sqrt{2}} \\ \text{or,}~~ a=\frac{5+15}{2\sqrt{2}}=\frac{20}{2\sqrt{2}}=5\sqrt{2}~~[\because~ a >0]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-81d10bb8e86e65b32eeb75b2f84c781a_l3.png)
![]()
Hence ![]()
For Full Solution PDF of the Ellipse ( S N De-Chhaya Mathematics ), click here.
5. The co-ordinates of the centre and of a vertex of an ellipse are ![]() and
and ![]() and its eccentricity is
and its eccentricity is ![]() find the equation of the ellipse.
find the equation of the ellipse.
Solution.
The centre ![]() and the vertex of the ellipse is
and the vertex of the ellipse is ![]() and
and ![]() respectively. Since the abscissa of the centre and vertex of the ellipse are equal, the major axis of the ellipse is parallel to
respectively. Since the abscissa of the centre and vertex of the ellipse are equal, the major axis of the ellipse is parallel to ![]() -axis. Hence, the equation of the ellipse can be taken in the form
-axis. Hence, the equation of the ellipse can be taken in the form
![]()
Now, by question, vertex : ![]()
![Rendered by QuickLaTeX.com \therefore~ \beta+a=4 \\ \text{or,}~~ -2+a=4~~[~\because\beta=-2] \\ \text{or,}~~ -2+a=4 \\ \text{or,}~~ a=4+2=6.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-7dd834e9c92d9e6a093b18ffcb31e54f_l3.png)

Hence by ![]() we get the required equation of ellipse
we get the required equation of ellipse
![]()
6(i) The vertices of an ellipse are ![]() and
and ![]() If the eccentricity of an ellipse be
If the eccentricity of an ellipse be ![]() find its equation.
find its equation.
Solution.
Since the ordinates of the two vertices of the ellipse are equal, the equation of the ellipse can be taken in the form :
![]()
So, the co-ordinates of the vertices of the ellipse ![]() are
are ![]()
![]()
From ![]() and
and ![]() we get,
we get,
![]()
Similarly, ![]()

Hence, the equation of the ellipse is given by

Read More :
- Careers
- Circle
- Co-ordinate Geometry
- Differentiation
- ellipse
- Hyperbola
- Integration By Parts
- Keto Guides
- Mathematics
- Parabola
- Parts of Speech
- Plane
- Renderforest
- S N De Class 12 Math Solution
- Self-Improvement
- Sentence and its Classification
- Straight Line
- Tangent and Normal
- Vector Products
(ii) Find the equation of the ellipse whose foci are ![]() and
and ![]() and whose semi-minor axis is
and whose semi-minor axis is ![]()
Solution.
The co-ordinates of foci of the given ellipse are
![]()
So, ![]()
The distance between the two foci is
![]()
From the co-ordinates of the foci of the ellipse, we can clearly say that the major axis of the ellipse is parallel to the ![]() -axis.
-axis.
So, the equation of the ellipse can be taken in the form :
![]()
So, the length of semi-minor axis is ![]() unit, so
unit, so ![]()
By ![]() we get,
we get,

Hence, using ![]() we get the required equation of ellipse
we get the required equation of ellipse
![]()
(iii) The eccentricity of an ellipse is ![]() and the co-ordinates of its one focus and the corresponding vertex are
and the co-ordinates of its one focus and the corresponding vertex are ![]() and
and ![]() respectively. Find the equation of the ellipse . Also find the co-ordinate of the point of intersection of its major axis and the directrix in the same direction.
respectively. Find the equation of the ellipse . Also find the co-ordinate of the point of intersection of its major axis and the directrix in the same direction.
Solution.
Since the ordinates of the given focus and vertex of the ellipse are equal, hence its major axis is parallel to ![]() -axis. Therefore, let us assume that the equation of the required ellipse be
-axis. Therefore, let us assume that the equation of the required ellipse be
![]()
The co-ordinates of one focus and the corresponding vertex of the ellipse ![]() are
are ![]() and
and ![]() respectively. By question,
respectively. By question, ![]()

![]()
Solving ![]() and
and ![]() we get,
we get, ![]()
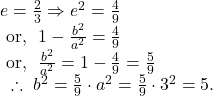
So, by ![]() we can say that the equation of the ellipse is
we can say that the equation of the ellipse is
![]()
2nd Part :
The equation of the major axis : ![]()
The directrix of the ellipse :

Hence, the co-ordinates of the point of intersection of its major axis and the directrix in the same direction : ![]()
7. The distance of a point of the ellipse ![]() from the centre
from the centre ![]() find the eccentric angle of the point.
find the eccentric angle of the point.
Solution.
The equation of the given ellipse is

Any point on the ellipse ![]() can be taken as
can be taken as ![]() where
where ![]() is the eccentric angle of that point.
is the eccentric angle of that point.
Now, since the distance of the point of the point of the given ellipse from the centre is ![]()
