In the previous article , we have solved few Short Answer Type questions of Hyperbola chapter of S.N.Dey mathematics, Class 11. In this article , we will solve Complete Long Answer Type questions of Hyperbola related problems of S N Dey mathematics class 11.

1. Find the centre, the length of latus rectum, the eccentricity, the co-ordinates of foci and the equations of the directrices of the hyperbola ![]()
Solution.
Comparing the given equation of hyperbola with the general form of hyperbola ![]() we get,
we get,
![]()
(i) The co-ordinates of centre of hyperbola : ![]()
(ii) The eccentricity ![]()
(iii) The co-ordinates of foci :
![]() i.e.,
i.e., ![]() and
and ![]()
(iv) The equations of directrices are :
![]()
2. Show that the equation ![]() represents the equation of a hyperbola ; find the co-ordinates of its centre and foci and also the equation of its directrices.
represents the equation of a hyperbola ; find the co-ordinates of its centre and foci and also the equation of its directrices.
Solution.
The equation of the hyperbola can be written as

Comparing the given equation of hyperbola with the general form of hyperbola ![]() we get,
we get,
![]()
(i) Centre : ![]()
(ii) Foci : ![]() i.e.,
i.e., ![]() and
and ![]()
The eccentricity ![]()
(iii) The equations of directrices are given by
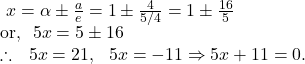
3. Find (i) the centre (ii) the vertice (iii) the equations of the axes (iv) the lengths of axes (v) the eccentricities (vi) the lengths of latera recta (vii) the co-ordinates of foci (viii) the equations of the directrices of the following two hyperbolas :
![]()
Solution.
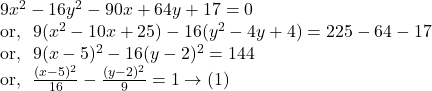
Comparing ![]() with
with ![]() we get,
we get,
![]()
(i) Centre of the hyperbola ![]() is
is ![]()
(ii) Co-ordinates of vertices : ![]()
(iii) The equation of transverse axis : ![]() and conjugate axis :
and conjugate axis : ![]()
(iv)The length of transverse axis : ![]() and the length of conjugate axis :
and the length of conjugate axis : ![]()
(v) The eccentricity ![]() is given by
is given by
![]()
(vi) The length of latera recta : ![]()
(vii) The co-ordinates of foci :
![]()
(viii) The equations of directrices are given by
![]()
Solution (b)
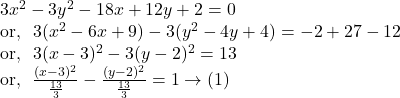
Comparing ![]() with
with ![]() we get,
we get,
![]()
(i) Centre of the hyperbola ![]() is
is ![]()
(ii) Co-ordinates of vertices : ![]()
(iii) The equation of transverse axis : ![]() and conjugate axis :
and conjugate axis : ![]()
(iv)The length of transverse axis : ![]() the length of conjugate axis :
the length of conjugate axis : ![]()
(v) The eccentricity ![]() is given by
is given by
![]()
(vi) The length of latera recta : ![]()
(vii) The co-ordinates of foci :
![]()
(viii) The equations of directrices are given by
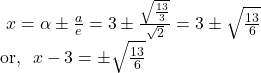
4. A point moves on a plane in such a manner that the difference of its distances from the points ![]() and
and ![]() is always constant and equal to
is always constant and equal to ![]() . Show that the locus of the moving point is a rectangular hyperbola whose equation you are to determine.
. Show that the locus of the moving point is a rectangular hyperbola whose equation you are to determine.
Solution.
Let the co-ordinates of moving point be ![]()
So, by question,
![Rendered by QuickLaTeX.com |\sqrt{(h-4)^2+k^2}-\sqrt{(h+4)^2+k^2}|=4\sqrt{2} \\ \text{or,}~~\sqrt{(h-4)^2+k^2}=\sqrt{(h+4)^2+k^2} \pm 4\sqrt{2} \\ \text{or,}~~(h-4)^2+k^2=(h+4)^2+k^2 +(4\sqrt{2})^2 \pm 8\sqrt{2} \sqrt{(h+4)^2+k^2} \\ \text{or,}~~ -[(h+4)^2-(h-4)^2]=32 \pm 8\sqrt{2}p~~(*) \\ \text{or,}~~ -4 \cdot h \cdot 4=32 \pm 8\sqrt{2}p \\ \text{or,}~~ -16h=32 \pm 8\sqrt{2}p \\ \text{or,}~~ -2h= 4 \pm \sqrt{2}p \\ \text{or,}~~ -(2h+4)=\pm \sqrt{2}p \\ \text{or,}~~ (2h+4)^2=2p^2 \\ \text{or,}~~ 4h^2+2 \cdot 2h \cdot 4+4^2=2(h+4)^2+2k^2 \\ \text{or,}~~ 2h^2+8h+8=(h+4)^2+k^2 \\ \text{or,}~~ 2h^2+8h+8=h^2+8h+16+k^2 \\ \therefore~h^2-k^2=8 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-7ff54bb2debb9fed7c1a26e8c244466e_l3.png)
Hence, by ![]() we can say that the locus of moving point is
we can say that the locus of moving point is ![]() which is a rectangular hyperbola.
which is a rectangular hyperbola.
Note ![]()
5. A point moves on a plane so that its distance from the line ![]() Show that the locus of the moving point is a hyperbola and the equation of its locus is
Show that the locus of the moving point is a hyperbola and the equation of its locus is ![]()
Solution.
Let the co-ordinates of the moving point be ![]()
So, by question,
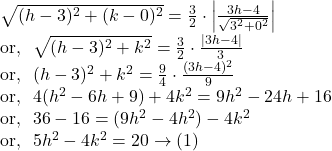
Hence, by ![]() we can say that the locus of the moving point represents a hyperbola and is given by
we can say that the locus of the moving point represents a hyperbola and is given by ![]()
6. The hyperbola ![]() passes through the point of intersection of the lines
passes through the point of intersection of the lines ![]() and
and ![]() and the length of its latus rectum is
and the length of its latus rectum is ![]() Find the co-ordinates of its foci.
Find the co-ordinates of its foci.
Solution.
The given equations of straight lines are ![]() and
and ![]()
From ![]() and
and ![]() we get,
we get,
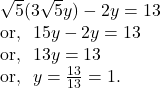
![]()
So, the point of intersection of the straight lines ![]() and
and ![]() is given by
is given by ![]()
Since the given hyperbola passes through the point ![]()
![]()
Again, the length of the latus rectum of the hyperbola is
![]()
From ![]() and
and ![]() we get,
we get,

![]()

Hence, the co-ordinates of the foci are
![]()
7. The numerical value of the product of the perpendicular distances of a moving point from the lines ![]() and
and ![]() is
is ![]() Find the equation to the locus of the moving point.
Find the equation to the locus of the moving point.
Solution.
Comparing the given ellipse with the general equation of the ellipse ![]() we get,
we get, ![]()
The eccentricity ![]() of the given ellipse is
of the given ellipse is
![]()
The co-ordinates of foci of the ellipse are ![]()
Let the co-ordinates of the moving point be ![]()
So, by question

Hence, the locus of the moving point is given by ![]() or,
or, ![]()
8. An ellipse ![]() has the equation
has the equation ![]() and
and ![]() and
and ![]() are its centre and focus in the usual notation. A hyperbola
are its centre and focus in the usual notation. A hyperbola ![]() has a vertex at
has a vertex at ![]() , has the point
, has the point ![]() as its focus nearer to
as its focus nearer to ![]() and has its latus rectum of equal length to that of
and has its latus rectum of equal length to that of ![]() Show that
Show that ![]() has the eccentricity
has the eccentricity ![]() and find its equation.
and find its equation.
Solution.
The given ellipse ![]()
The eccentricity ![]() of
of ![]() is
is
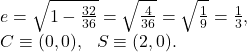
The transverse axis of ![]() is along
is along ![]() axis and the conjugate axis of H is along
axis and the conjugate axis of H is along ![]() -axis. Let the eccentricity of H be
-axis. Let the eccentricity of H be ![]() the length of the transverse axis be
the length of the transverse axis be ![]() and the length of the conjugate axis be
and the length of the conjugate axis be ![]()
![]() Focus of H is
Focus of H is ![]() and the vertex
and the vertex ![]() and so clearly, the ordinates of centre of
and so clearly, the ordinates of centre of ![]() is
is ![]()
By question, ![]() and
and
![]()
Again, the length of latus rectum of ![]() is = the length of latus rectum of
is = the length of latus rectum of ![]() .
.

For the hyperbola, the eccentricity ![]() is
is
![Rendered by QuickLaTeX.com e_1=1+\frac{b_1^2}{a_1^2} \Rightarrow e_1^2-1=\frac{b_1^2}{a_1^2} \Rightarrow \frac{b_1^2}{a_1}=a_1(e_1^2-1)=\frac{16}{3} \\ \therefore~ a_1(e_1-1) \times (e_1+1)=\frac{16}{3} \\ \text{or,}~~ 2(e_1+1)=\frac{16}{3}~~[\text{By (1)}] \\ \text{or,}~~ e_1+1=\frac 83 \Rightarrow e_1=\frac 83-1=\frac 53.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-9d72c8819791c09026729d1ced629348_l3.png)
![]()

![]()
hence, the equation of required hyperbola is
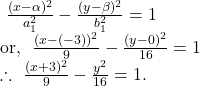
9. The foci of the ellipse ![]() coincide with the hyperbola. If
coincide with the hyperbola. If ![]() for hyperbola, find the equation of the hyperbola.
for hyperbola, find the equation of the hyperbola.
Solution.
The given equation of ellipse is ![]()
Comparing ![]() with
with ![]() we get,
we get,
![]()
The eccentricity of ![]() is given by
is given by
![]()
The co-ordinates of foci of the ellipse
![]()
Let the equation of the hyperbola be ![]()
The eccentricity of the hyperbola ![]() . Since the foci of the ellipse
. Since the foci of the ellipse ![]() coincide with the hyperbola
coincide with the hyperbola ![]() , so
, so
![]()
For the hyperbola ![]() we get,
we get,

Hence, by ![]() , the equation of required hyperbola is
, the equation of required hyperbola is
![]()
Solution.
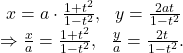
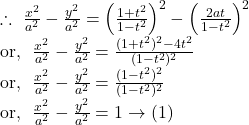
Clearly, the equation ![]() represents a hyperbola whose eccentricity is given by
represents a hyperbola whose eccentricity is given by ![]()