In the previous article , we have solved few Short Answer Type questions of Hyperbola chapter of S.N.Dey mathematics, Class 11. In this article , we will solve few more Short Answer Type questions of Hyperbola related problems of S N Dey mathematics class 11.

6. Find the equation of the hyperbola, referred to its axes as lines parallel to co-ordinate axes and having centre at ![]() eccentricity
eccentricity ![]() and the length of latus rectum
and the length of latus rectum ![]() .
.
Solution.
The equation of the hyperbola having centre at ![]() and axes parallel to co-ordinate axes can be written as
and axes parallel to co-ordinate axes can be written as
![]()
The length of latus rectum ![]()

![]()
Hence, by ![]() the required equation of hyperbola is given by
the required equation of hyperbola is given by
![]()
7. The distance between the vertices of a hyperbola is half the distance between its foci and the length of its semi-conjugate axis is ![]() . Referred to its axes as axes of co-ordinates, find the equation of the hyperbola.
. Referred to its axes as axes of co-ordinates, find the equation of the hyperbola.
Solution.
We know that the distance between the vertices of the hyperbola is ![]() unit and the distance between the foci is
unit and the distance between the foci is ![]() unit.
unit.
By question, ![]()
Again, the length of semi-conjugate axis ![]()
Now, ![]()
Hence, the equation of the required hyperbola is
![]()
8. The co-ordinates of the foci of a hyperbola are ![]() and
and ![]() and its eccentricity is
and its eccentricity is ![]() find the equation of the hyperbola and the length of its latus rectum.
find the equation of the hyperbola and the length of its latus rectum.
Solution.

![]()
Now, the centre of the hyperbola is the mid-point of the foci i.e., ![]()
From the co-ordinates of the foci, we can notice that the transverse axis of the hyperbola is along ![]() -axis and so the equation of the hyperbola having centre at
-axis and so the equation of the hyperbola having centre at ![]() is
is
![]()
Computer Science with Python Textbook for Class 11 Paperback
Product details
Publisher : Dhanpat Rai & Co.; 2020th edition (1 January 2020); Dhanpat Rai & Co.
Language : English
Paperback : 574 pages
ISBN-10 : 8177002309
ISBN-13 : 978-8177002300
Item Weight : 295 g
Dimensions : 20.3 x 25.4 x 4.7 cm
Country of Origin : India
Generic Name : BOOK
9. The centre of a hyperbola is at ![]() , the co-ordinates of one of its vertices are
, the co-ordinates of one of its vertices are ![]() and eccentricity is
and eccentricity is ![]() find its equation.
find its equation.
Solution.
If ![]() is the distance of the vertex from the centre , then
is the distance of the vertex from the centre , then
![]()
Again, ![]()
Since the ordinates of the centre and the vertex of the hyperbola is ![]() , both cantre and the vertex lie on the straight line
, both cantre and the vertex lie on the straight line ![]()
So, the transverse axis of the hyperbola is parallel to ![]() -axis. So, the equation of the hyperbola with centre
-axis. So, the equation of the hyperbola with centre ![]() is
is

10. Find the equation of the hyperbola with centre at the origin, transverse axis on ![]() -axis, passing through the point
-axis, passing through the point ![]() and having the length of semi-conjugate axis
and having the length of semi-conjugate axis ![]()
Solution.
The hyperbola having centre at the origin and transverse axis on ![]() -axis, can be written in the form of
-axis, can be written in the form of ![]()
Since the hyperbola ![]() passes through the point
passes through the point ![]()
![Rendered by QuickLaTeX.com \therefore~\frac{(3\sqrt{2})^2}{a^2}-\frac{(-2)^2}{b^2}=1 \\ \text{or,}~\frac{18}{a^2}-\frac{4}{2^2}=1~~[~\because~ b=2~] \\ \text{or,}~~ \frac{18}{a^2}-1=1 \\ \text{or,}~~\frac{18}{a^2}=1+1 \\ \text{or,}~~a^2=\frac{18}{2}=9 .](https://examhoop.com/wp-content/ql-cache/quicklatex.com-2bb20a82e331bd4a0ad671553c1e4baa_l3.png)
Hence, putting the values of ![]() and
and ![]() in
in ![]() , we get the required equation of hyperbola which is given by
, we get the required equation of hyperbola which is given by
![]()
11. The lengths of transverse and conjugate axes of a hyperbola are ![]() unit and
unit and ![]() unit respectively and their equations are
unit respectively and their equations are ![]() and
and ![]() find the equation of the hyperbola.
find the equation of the hyperbola.
Solution.
It is given that ![]()
Since the transverse and conjugate axes of the hyperbola are ![]() and
and ![]() , the point of intersection of
, the point of intersection of ![]() and
and ![]() is given by
is given by ![]() which is the centre of the hyperbola.
which is the centre of the hyperbola.
Since the transverse axis of the hyperbola given by ![]() is parallel to
is parallel to ![]() -axis, so the equation of the hyperbola with centre
-axis, so the equation of the hyperbola with centre ![]() is given by
is given by
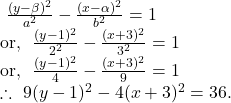
12. ![]() and
and ![]() are respectively the eccentricities of a hyperbola and its conjugate. Prove that,
are respectively the eccentricities of a hyperbola and its conjugate. Prove that, ![]()
Solution.
Let the equation of the hyperbola be ![]()
The equation of the conjugate hyperbola of ![]() can be written as
can be written as ![]()
![]()
![]()
13. Find the eccentricity of the hyperbola ![]() If
If ![]() are the foci and
are the foci and ![]() any point on this hyperbola, prove that,
any point on this hyperbola, prove that, ![]() (
( ![]() is the origin).
is the origin).
Solution.
![]()
Comparing ![]() with the general equation of hyperbola
with the general equation of hyperbola ![]() we get
we get ![]()
![]()
The co-ordinates of foci of the hyperbola ![]() are
are ![]() i.e.,
i.e., ![]()
![]()
The co-ordinates of any point ![]() on the hyperbola
on the hyperbola ![]() can be taken as
can be taken as ![]()
![]()
Let ![]() so that
so that ![]()
![]()
Now, ![]()
![Rendered by QuickLaTeX.com \therefore~ \overline{SP}^2 \cdot \overline{S_1P}^2\\=[(c-\sqrt{2})^2+d^2] \cdot [(c+\sqrt{2})^2+d^2]\\=(c-\sqrt{2})^2(c+\sqrt{2})^2+d^2[(c+\sqrt{2})^2+(c-\sqrt{2})^2]+d^4\\=(c^2-2)^2+d^2[2(c^2+2)]+d^4\\=c^4-4c^2+4+2d^2(c^2+2)+d^4\\=c^4+2c^2d^2+d^4-4(c^2-1)+4d^2\\=(c^2+d^2)^2-4d^2+4d^2~~[\text{By (3)}]\\=(c^2+d^2)^2 \\ \text{or,}~~ \overline{SP}\cdot \overline{S_1P}=(c^2+d^2)=\sec^2\theta+\tan^2\theta \rightarrow(4)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-e07de059dcf5cf7971dd6b88dd60bc16_l3.png)
Hence by ![]() and
and ![]() , the result follows.
, the result follows.
14. ![]() is a variable point on the hyperbola
is a variable point on the hyperbola ![]() and
and ![]() is a fixed point. Show that the locus of the middle point of the line segment
is a fixed point. Show that the locus of the middle point of the line segment ![]() is another rectangular hyperbola.
is another rectangular hyperbola.
Solution.
![]()
The co-ordinates of any point ![]() on the hyperbola
on the hyperbola ![]() can be written as
can be written as ![]()
Let the middle point of ![]() be
be ![]()
![]()
From ![]() and
and ![]() we get,
we get,
![]()
![]()
So, by ![]() we can say that the locus of the middle point of the line segment
we can say that the locus of the middle point of the line segment ![]() is
is
![]()
Since the equation ![]() is a rectangular hyperbola, so the result follows.
is a rectangular hyperbola, so the result follows.
15. Show that the difference of focal distances of any point of the hyperbola ![]() is constant.
is constant.
Solution.
![]()
Comparing ![]() with the standard form of the hyperbola
with the standard form of the hyperbola ![]() , we get
, we get

Now, the co-ordinates of foci are given by
![]()
Let any point on the hyperbola ![]() be
be ![]()

Similarly, we can easily show that
![]()
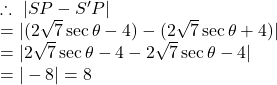
Hence, the difference of focal distances of any point of the given hyperbola is constant.
16. The co-ordinates of the foci of a hyperbola are ![]() and the length of its latus rectum is
and the length of its latus rectum is ![]() unit; find its equation.
unit; find its equation.
Solution.
By question, we notice that the co-ordinates of the foci ![]() lie on the
lie on the ![]() -axis. Now, the transverse axis of the hyperbola is along
-axis. Now, the transverse axis of the hyperbola is along ![]() -axis.
-axis.
![]() The equation of the hyperbola can be written as
The equation of the hyperbola can be written as ![]()
Now, ![]()
![Rendered by QuickLaTeX.com ~2ae=\sqrt{(0-0)^2+(4+4)^2}=8 \\ \text{or,}~~ ae=\frac 82=4 \\ \text{or,}~~ a^2e^2=4^2 \\ \text{or,}~~ a^2 \left(1+\frac{b^2}{a^2}\right)=16 \\ \text{or,}~~ a^2+b^2=16 \\ \text{or,}~~ a^2+6a=16~~[\text{By (2)}] \\ \text{or,}~~ a^2+6a-16=0 \\ \text{or,}~~ a^2+8a-2a-16=0 \\ \text{or,}~~ a(a+8)-2(a+8)=0 \\ \text{or,}~~(a+8)(a-2)=0 \\ \text{or,}~~ a=2~~[~\because a>0~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-59301228ff27494c1eb6ed116ac37b6c_l3.png)
![]()
So, the equation of the hyperbola is given by
![]()
The eccentricity of the hyperbola ![]() is
is
![]()
17. Show that for all values of ![]() the point
the point ![]() lies on a fixed hyperbola. What is the value of the eccentricity of the hyperbola.
lies on a fixed hyperbola. What is the value of the eccentricity of the hyperbola.
Solution.

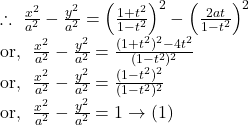
Clearly, the equation ![]() represents a hyperbola whose eccentricity is given by
represents a hyperbola whose eccentricity is given by ![]()

