In the previous article, we discussed Short Answer Type Questions of Vector Product. In this article, we will discuss the solutions of Long Answer Type Questions (1-11) of Ex-2A in the chapter Product of Two Vectors as given in the Chhaya Publication Book of aforementioned chapter of S N De book.

Vector Product | S N Dey mathematics class 12 Solutions of Ex-2A
![]() Applying vectors, show that
Applying vectors, show that
![]()
Solution.
let ![]()
![Rendered by QuickLaTeX.com \text{We know,}~~~\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos\theta \\ \text{or,}~~ \vec{a} \cdot \vec{b} \leq|\vec{a}||\vec{b}| ~~~[\because~~\cos\theta \leq 1] \\ \text{or,}~~(a_1\hat{i}+a_2\hat{j} +a_3\hat{k}) \cdot (b_1\hat{i}+b_2\hat{j} +b_3\hat{k}) \\~~\leq \sqrt{a_1^2+a_2^2+a_3^2}\cdot \sqrt{b_1^2+b_2^2+b_3^2} \\ \text{or,}~~a_1b_1+a_2b_2+a_3b_3 \leq \sqrt{a_1^2+a_2^2+a_3^2}\cdot \sqrt{b_1^2+b_2^2+b_3^2} \\ \text{or,}~~ (a_1b_1+a_2b_2+a_3b_3)^2 \leq (a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)~~~\text{(showed)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-f3e96f630966784599d5bf9995d74d30_l3.png)
![]() By vector method show that,
By vector method show that,
![]() an angle inscribed in a semi- circle is a right angle.
an angle inscribed in a semi- circle is a right angle.
Solution.
let ![]() be the inscribed angle .
be the inscribed angle .
To prove : ![]()
![]() is the diameter and
is the diameter and ![]() is the center of the semi-circle.
is the center of the semi-circle.
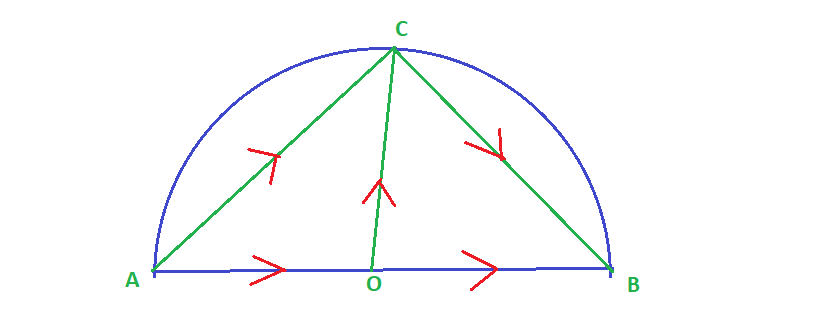
Now, by the law of triangle of vectors, we get
![]()
![]()
Hence, by ![]() and
and ![]() we get,
we get,
![Rendered by QuickLaTeX.com \vec{AC} \cdot \vec{CB}\\=(\vec{OB}+\vec{OC}) \cdot (\vec{OB}-\vec{OC}) \\=|\vec{OB}|^2-|\vec{OC}|^2 \\= 0~~[~\because~~ |\vec{OB}|=|\vec{OC}|=\text{radius}] \\~~\\ ~ \therefore~~ \vec{AC} \cdot \vec{CB}=0 \\ \Rightarrow ~ \vec{AC} \perp \vec{CB}.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-dfae789123953c3cb2213614660c60ec_l3.png)
![]()
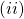 the parallelogram whose diagonals are equal is a rectangle.
the parallelogram whose diagonals are equal is a rectangle.
Solution.
let ![]() be a parallelogram and
be a parallelogram and ![]()
![Rendered by QuickLaTeX.com \therefore~|\vec{AC}|^2=|\vec{BD}|^2 \\ \text{or,}~~ |\vec{AB}+\vec{BC}|^2=|\vec{BC}+\vec{CD}|^2 \\ \text{or,}~~ |\vec{AB}+\vec{BC}|^2=|\vec{BC}-\vec{AB}|^2 ~~[\because~~\vec{CD}=-\vec{AB}] \\ \text{or,}~~ |\vec{AB}|^2+|\vec{BC}|^2+2\vec{AB}\cdot \vec{BC}=|\vec{BC}|^2+|\vec{AB}|^2-2\vec{BC}\cdot \vec{AB} \\ \text{or,}~~ 2\vec{AB}\cdot \vec{BC}=-2\vec{AB}\cdot \vec{BC} \\ \text{or,}~~ 4\vec{AB}\cdot \vec{BC}=0 \\ \text{or,}~~ \vec{AB}\cdot \vec{BC}=0\\ \text{So,}~~\vec{AB} \perp \vec{BC}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-108d01acd506697eb7ace050c81429eb_l3.png)
Hence, ![]() is a parallelogram.
is a parallelogram.
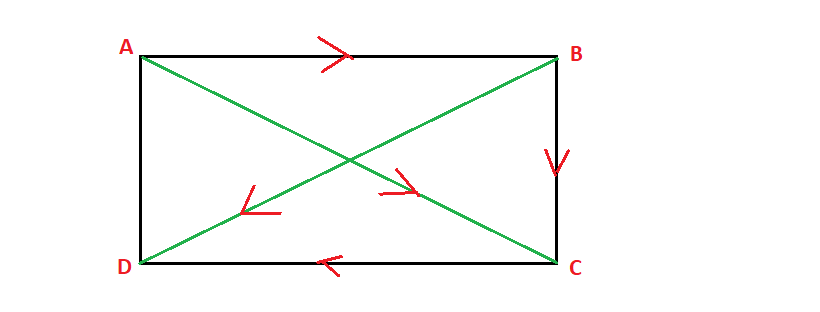
 the perpendicular bisectors of the sides of a triangle are concurrent.
the perpendicular bisectors of the sides of a triangle are concurrent.
Solution.
let ![]() be the perpendicular bisectors of the sides
be the perpendicular bisectors of the sides ![]() respectively, where
respectively, where ![]() be the point of intersection of
be the point of intersection of ![]()
Suppose that position vectors of ![]() with respect to
with respect to ![]() are
are ![]() respectively.
respectively.
Let ![]() be the midpoint of
be the midpoint of ![]() and so the position vectors of
and so the position vectors of ![]() are
are ![]() respectively.
respectively.
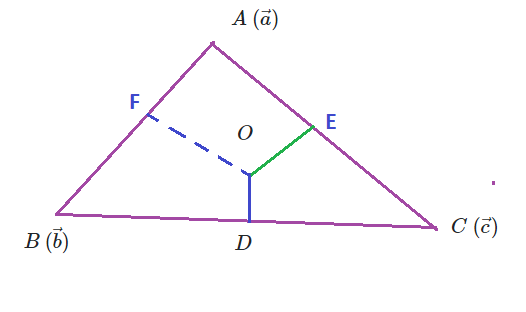
We have to prove that ![]()

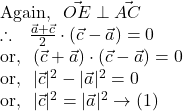
Hence, from ![]() and
and ![]() we get,
we get,

Hence, the perpendicular bisectors of the sides of a triangle are concurrent.
![]() medium to the base of an isoscales triangle is perpendicular to the base.
medium to the base of an isoscales triangle is perpendicular to the base.
Solution.
let ![]() is an isoscales triangle where
is an isoscales triangle where ![]()
Suppose that the position vectors of ![]() with respect to
with respect to ![]() are
are ![]() respectively,
respectively, ![]() being the origin.
being the origin.
![]()
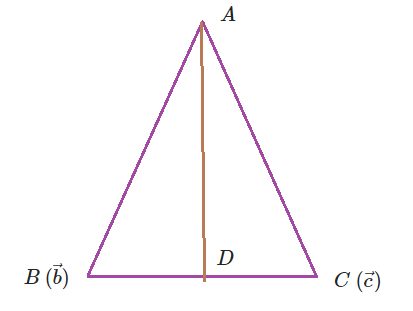
let ![]() be the mid point of the base
be the mid point of the base ![]() so that
so that ![]()
Also, by ![]() we get,
we get, ![]()
![Rendered by QuickLaTeX.com \therefore~~ \vec{BC} \cdot \vec{AD} \\~~\\~~~~= (\vec{c}-\vec{b}) \cdot \left(\frac{\vec{b}+\vec{c}}{2}\right) \\~~~~= \frac 12[(\vec{c}-\vec{b}) \cdot (\vec{c}+\vec{b})] \\~~~~= \frac 12[|\vec{c}|^2-|\vec{b}|^2] \\~~~~= \frac 12[|\vec{c}|^2-|\vec{c}|^2]~~[\text{By (2)}]\\~~~~= 0 \\~~ \\ \text{So,}~~ \vec{BC} \perp \vec{AD}.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-9d9fb22005896dab5732a5bfbfb51871_l3.png)
Hence follows the result.
![]() are three given points. Find the angle between the vectors
are three given points. Find the angle between the vectors ![]()
Solution.
By the question, the position vectors of ![]() are given by
are given by ![]()
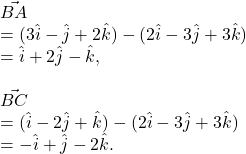
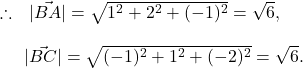

If ![]() is the angle between the vectors
is the angle between the vectors ![]()

![]() Three vectors
Three vectors ![]() are such that
are such that ![]() if
if ![]() and
and ![]() then find the value of
then find the value of ![]()
Solution.

![]() The scalar product of the vector
The scalar product of the vector ![]() with the unit vector along the sum of vectors
with the unit vector along the sum of vectors ![]() is equal to one. Find the value of
is equal to one. Find the value of ![]()
Solution.
![]()

Now, the unit vector along the sum of vectors ![]() is given by :
is given by :
![]()
By question,

![]() Let
Let ![]() and
and ![]() be three given vectors ; If
be three given vectors ; If ![]() and
and ![]() are perpendicular to each other , find
are perpendicular to each other , find ![]()
Solution.
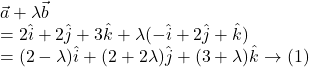
![]()
If ![]() and
and ![]() are perpendicular to each other , then
are perpendicular to each other , then
![Rendered by QuickLaTeX.com (\vec{a}+\lambda \vec{b}) \cdot \vec{c}=0 \\ \text{or,}~~ 3(2-\lambda)+(2+2\lambda)+0=0 ~~[\text{By (1),(2)} ] \\ \text{or,}~~ 6-3\lambda+2+2\lambda=0 \\ \text{or,}~~ 8-\lambda=0 \\ \text{or,}~~ \lambda=8 ~~~~ \text{(ans.)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-cffbd8158749587c09fcb195a7563bfb_l3.png)
![]() Let
Let ![]() and
and ![]() Find a vector
Find a vector ![]() which is perpendicular to both
which is perpendicular to both ![]()
Solution.
We know that ![]() denotes a vector which is perpendicular to both
denotes a vector which is perpendicular to both ![]() and
and ![]()

By the question and using ![]() we can say that
we can say that
![]() where
where ![]() is any scalar, so that
is any scalar, so that

![Rendered by QuickLaTeX.com ~\therefore~~\vec{d}\\=\lambda(32\hat{i}-\hat{j}-14\hat{k})\\=2(32\hat{i}-\hat{j}-14\hat{k})~~[\text{By (2)}]\\=64\hat{i}-2\hat{j}-28\hat{k} ~~\text{(ans.)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c394bcbe6a4d487634c56dcb01e5c9ad_l3.png)
![]() If
If ![]() and
and ![]() are the position vectors of points
are the position vectors of points ![]() and
and ![]() respectively, then find the angle between
respectively, then find the angle between ![]() and
and ![]() Deduce that
Deduce that ![]() and
and ![]() are collinear.
are collinear.
Solution.


If ![]() be the angle between
be the angle between ![]() and
and ![]() then
then
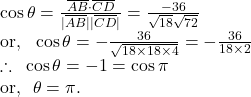

Hence, we can deduce that ![]() and
and ![]() are collinear.
are collinear.
![]() Express the vector
Express the vector ![]() as sum of two vectors such that one is parallel to the vector
as sum of two vectors such that one is parallel to the vector ![]() and the other is perpendicular to
and the other is perpendicular to ![]()
Solution.
Let ![]() where
where ![]() is parallel to
is parallel to ![]() and
and ![]()
Since ![]() is parallel to
is parallel to ![]() so that
so that ![]() , where
, where ![]() is a non-zero scalar.
is a non-zero scalar.

Since ![]()
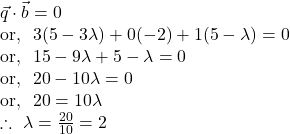
Hence, by ![]() we get by putting the value of
we get by putting the value of ![]()
![]()
![]()
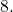 If
If  then
then  show by an example that the converse of this statement is not always true.
show by an example that the converse of this statement is not always true.
Solution.
Let ![]()
Here, clearly ![]() but
but

Hence by ![]() the result follows.
the result follows.
![]() If
If ![]() and
and ![]() find the vector
find the vector ![]() which is perpendicular to both
which is perpendicular to both ![]() and
and ![]() and which satisfies the relation
and which satisfies the relation ![]()
Solution.
let ![]()
By question,
![]()

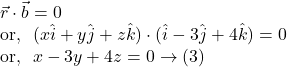
From ![]() and
and ![]() we get by cross multiplication,
we get by cross multiplication,
![Rendered by QuickLaTeX.com \frac{x}{16-3}=\frac{y}{-1-12}=\frac{1}{-9-4} \\ \text{or,}~~ \frac{x}{13}=\frac{y}{-13}=\frac{z}{-13}=\lambda~ ~[\neq 0~~ \text{(say)}] \\~~\\ \therefore~~ x= 13 \lambda,~~y=-13\lambda,~~z=-13\lambda ~\rightarrow(4)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-1dbeefeb70b9ed11ce1445d5f6950581_l3.png)

![]()
![]() Let
Let ![]() be the position vectors of the vertices of a triangle ; prove that the area of the triangle is
be the position vectors of the vertices of a triangle ; prove that the area of the triangle is ![]()
Solution.
Area of ![]() is given by :
is given by :

![]() Given
Given ![]() If
If ![]() and
and ![]() is perpendicular to
is perpendicular to ![]() and
and ![]() find in component form the vector
find in component form the vector ![]()
Solution.
We first compute the value of ![]()

If ![]() is perpendicular to
is perpendicular to ![]() and
and ![]() then
then
![Rendered by QuickLaTeX.com \vec{c}=\lambda(\vec{a} \times \vec{b}), ~~[~~\lambda \neq 0] \rightarrow(1)\\ ~\therefore~ |\vec{c}|=|\lambda| |\vec{a} \times \vec{b}| \\ \text{or,}~~ 21=|\lambda| \times 21\sqrt{3} \\ \text{or,}~~ |\lambda|=\frac{21}{21\sqrt{3}} \\ \text{or,}~~ |\lambda|=\frac{1}{\sqrt{3}} \\ \therefore~ \lambda=\pm \frac{1}{\sqrt{3}}.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-9a46d9c474cecc7e9e805dd8fa1c32a5_l3.png)
Hence, by ![]() we get
we get
