In the previous article , we have solve the solutions of Ex-2B of Vector Product chapter of S N Dey mathematics class 12 book of Chhaya maths. In this article, we will discuss the solutions of Ex-2B of Product of two vectors chapter.

Vector Product | S N Dey mathematics class 12 Solutions of Ex-2A
![]() If
If ![]() and
and ![]() find the value of
find the value of ![]()
Solution.
![Rendered by QuickLaTeX.com ~~ [\vec{b}~~\vec{c}~~\vec{a}]\\= \begin{vmatrix} 1 & -1 & 0 \\ 5 & 2 & 3 \\ 1& 1& 0 \\ \end{vmatrix} \\ = 1\begin{vmatrix} 2& 3 \\ 1 & 0 \\ \end{vmatrix}+1\begin{vmatrix} 5 & 3 \\ 1 & 0 \\ \end{vmatrix} \\= (0-3)+(0-3)\=-6~~\text{(ans.)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-44897638f0ce4a1c04677f562c357f3b_l3.png)
![]() If
If ![]() and
and ![]() find
find ![]()
Solution.
![Rendered by QuickLaTeX.com \vec{\alpha} \cdot (\vec{\beta} \times \vec{\gamma}) \\=[\vec{\alpha} ~~ \vec{\beta}~~\vec{\gamma}] \\= \begin{vmatrix} 1& -2 &3 \\ 2& -3&1 \\ 3&1 &-2 \\ \end{vmatrix} \\= 1(6-1)+2(-4-3)+3(2+9)\\=5-14+33\\=24~~\text{(ans.)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-2981c6037e29d87b87b767b2f9f79fd0_l3.png)
![]() If
If ![]() and
and ![]() find
find ![]()
Solution.
![Rendered by QuickLaTeX.com [\vec{c}~~\vec{a}~~\vec{b}] \\= \begin{vmatrix} 2& 1 & 3 \\ -1 & 2 & 1 \\ 3& 1 & 2 \\ \end{vmatrix} \\= 2\begin{vmatrix} 2& 1 \\ 1& 2 \\ \end{vmatrix}-1\begin{vmatrix} \\ -1 & 1 \\ 3& 2 \\ \end{vmatrix}+3\begin{vmatrix} -1& 2 \\ 3 & 1 \\ \end{vmatrix}\\=2(4-1)-1(-2-3)+3(-1-6) \\= 2 \times 3+5+3 \times (-7) \\=6+5-21\\=-10~~\text{(ans.)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-82a20815f1e8b87b47c97fc29fdc8aba_l3.png)
![]() The vectors which determine the sides of the parallelopiped are given below ; In each case find the volume of the parallelopiped .
The vectors which determine the sides of the parallelopiped are given below ; In each case find the volume of the parallelopiped .
![]()
Solution.
let ![]()
![Rendered by QuickLaTeX.com [\vec{c}~~\vec{a}~~\vec{b}] \\= \begin{vmatrix} 1& 1 &1 \\ 0&0 &1 \\ 3&-1 &2 \\ \end{vmatrix} \\ = -1 \begin{vmatrix} 1 & 1 \\ 3 &-1 \\ \end{vmatrix} \\= -1(-1-3) \\=4.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-411ee75081503962f6eac085e9d9e3e7_l3.png)
So, the volume of the parallelopiped is :
![]()
![]()
Solution.
Let ![]()
![Rendered by QuickLaTeX.com [\vec{a}~~\vec{b}~~\vec{c}] \\= \begin{vmatrix} 2 & -1 & 1 \\ 1 & 2 & -3 \\ 3 & -4& 5 \\ \end{vmatrix}\\=2\begin{vmatrix} 2& -3 \\ -4 & 5 \\ \end{vmatrix}+1\begin{vmatrix} 1 & -3 \\ 3 & 5 \\ \end{vmatrix}+1 \begin{vmatrix} 1 & 2 \\ 3 & -4 \\ \end{vmatrix}\\=2(10-12)+1(5+9)+1(-4-6)\\=-4+14-10\\=0](https://examhoop.com/wp-content/ql-cache/quicklatex.com-171dfbbb9c62357d014f71f54533047b_l3.png)
So, the volume of the parallelopiped is :
![]()
![]()
Solution.
Let ![]()
![Rendered by QuickLaTeX.com [\vec{a}~~\vec{b}~~\vec{c}] \\= \begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 2 \\ 1 & -2& 4 \\ \end{vmatrix} \\= 1\begin{vmatrix} 2& 2 \\ -2 & 4 \\ \end{vmatrix}-1\begin{vmatrix} 1 & 2 \\ 1 & 4 \\ \end{vmatrix}+1 \begin{vmatrix} 1 & 2 \\ 1 & -2 \\ \end{vmatrix}\\=1(8+4)-1(4-2)+1(-2-2)\\=12-2-4\\=6](https://examhoop.com/wp-content/ql-cache/quicklatex.com-91e198e1b9236c45bfcbe753679c96bf_l3.png)
So, the volume of the parallelopiped is :
![]()
![]() In each of the following show that the given vectors are coplanar.
In each of the following show that the given vectors are coplanar.
![]()
Solution.
Let ![]() Then,
Then,

Since ![]() hence the given vectors are coplanar.
hence the given vectors are coplanar.
![]()
Solution.

Since, ![]() hence the given vectors are coplanar.
hence the given vectors are coplanar.
![]()
Solution.

![Rendered by QuickLaTeX.com (\vec{a}-2\vec{b}+\vec{c}) \cdot [(2\vec{a}+\vec{b}-2\vec{c} )\times (3\vec{a}-\vec{b}-\vec{c})]\\= (\vec{a}-2\vec{b}+\vec{c}) \cdot [-5(\vec{a} \times \vec{b})-3(\vec{b} \times \vec{c})-4(\vec{c} \times \vec{a})] \\= -3 [\vec{a}~~\vec{b}~~\vec{c}]+8[\vec{b}~~\vec{c}~~\vec{a}]-5 [\vec{c}~~\vec{a}~~\vec{b}]~~[*]\\=0 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-0c62453e266c9ffb727daf9f3827ba47_l3.png)
Hence, from the result obtained from ![]() we can conclude that the given vectors are coplanar.
we can conclude that the given vectors are coplanar.
Note[*] : ![]()
![]() If
If ![]() find
find ![]() and interpret the result.
and interpret the result.
Solution.

Since, ![]() hence the given vectors are coplanar.
hence the given vectors are coplanar.
![]() If the vectors
If the vectors ![]() and
and ![]() are coplanar, find the value of
are coplanar, find the value of ![]()
Solution.
let ![]()
Since ![]() are coplanar,
are coplanar, ![]()

![]() If the vectors
If the vectors ![]() and
and ![]() are coplanar , find the value of
are coplanar , find the value of ![]()
Solution.
If the vectors ![]() are coplanar, then
are coplanar, then

To download full solution PDF of Products of Two Vectors (S N De) , click here .
![]() The position vectors of four points
The position vectors of four points ![]() and
and ![]() are given below. In each case, using vector method prove that the four points
are given below. In each case, using vector method prove that the four points ![]() and
and ![]() are coplanar.
are coplanar.
![]()
Solution.

![Rendered by QuickLaTeX.com [\vec{AB}~~\vec{BC}~~\vec{CD}]\\= \begin{vmatrix} -11& 7 &-20 \\ 9&-9 &0 \\ -4& 8 &20 \\ \end{vmatrix}\\=\begin{vmatrix} -15& 15&0 \\ 9 & -9 &0 \\ -4& 8 & 20 \\ \end{vmatrix} ~~[~R_1' \rightarrow R_1+R_3~]\\= 20(15 \times 9-15\times 9)\\=0](https://examhoop.com/wp-content/ql-cache/quicklatex.com-98da0f1690c5672f215336f9b874c448_l3.png)
![]() are coplanar and so, the four points
are coplanar and so, the four points ![]() and
and ![]() are coplanar.
are coplanar.
![]()
Solution.

![Rendered by QuickLaTeX.com [ \vec{AB}~~\vec{BC}~~\vec{CD}]\\= \begin{vmatrix} -2& -4 &-6 \\ 1&1 &-2 \\ 2& 3 &1 \\ \end{vmatrix}\\=-2(1+6)+4(1+4)-6(3-2)\\=-2\times 7+20-6\\=-14+20-6\\=0](https://examhoop.com/wp-content/ql-cache/quicklatex.com-06d34a0d8f73d6a11d0bb0aadc6e1f3c_l3.png)
![]() are coplanar and so, the four points
are coplanar and so, the four points ![]() and
and ![]() are coplanar.
are coplanar.
![]() If the vectors
If the vectors ![]() and
and ![]() are coplanar, then find the value of
are coplanar, then find the value of ![]()
Solution.
let ![]() and
and ![]()
If the vectors ![]() and
and ![]() are coplanar,
are coplanar,

![]() If the vectors
If the vectors ![]() and
and ![]() are coplanar, find
are coplanar, find ![]() in terms of
in terms of ![]()
Solution.
If the vectors ![]() are coplanar,
are coplanar,

![]() Prove that,
Prove that,
![]()
Solution.
![Rendered by QuickLaTeX.com (\vec{a}+\vec{b}) \cdot {(\vec{b}+\vec{c}) \times (\vec{c}+\vec{a})} \\= (\vec{a}+\vec{b}) \cdot (\vec{b} \times \vec{c}+\vec{b} \times \vec{a}+\vec{c}\times \vec{c}+\vec{c}\times \vec{a})\\= (\vec{a}+\vec{b}) \cdot (\vec{b} \times \vec{c}+\vec{b} \times \vec{a}+0+\vec{c}\times \vec{a})\\= (\vec{a}+\vec{b}) \cdot (\vec{b} \times \vec{c}+\vec{b} \times \vec{a}+\vec{c}\times \vec{a}) \\= [\vec{a}~~\vec{b}~~\vec{c}] +[\vec{a}~~\vec{b}~~\vec{a}] +[\vec{a}~~\vec{c}~~\vec{a}] +[\vec{b}~~\vec{b}~~\vec{c}] +[\vec{b}~~\vec{b}~~\vec{a}] +[\vec{b}~~\vec{c}~~\vec{a}] \\=[\vec{a}~~\vec{b}~~\vec{c}] +0+0+0+0+[\vec{a}~~\vec{b}~~\vec{c}] \\=2[\vec{a}~~\vec{b}~~\vec{c}] \\=2\vec{a} \cdot (\vec{b} \times \vec{c})~~\text{(proved)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-5c5c078b006bce883845db85ea1f57f2_l3.png)
![]()
Solution.
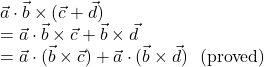
![]() and
and ![]() then find the value of
then find the value of ![]()
Solution.
![Rendered by QuickLaTeX.com [\vec{\alpha}~~\vec{\beta}~~\vec{\gamma}] =-10 \\ \text{or,}~~ \begin{vmatrix} \lambda & 1 & 3 \\ -1 &2 &1 \\ 3& 1&2 \\ \end{vmatrix} =-10 \\ \text{or,}~~ \lambda(4-1)-1(-2-3)+3(-1-6)=-10 \\ \text{or,}~~ 3\lambda+5-21=-10 \\ \text{or,}~~ 3\lambda-16=-10 \\ \text{or,}~~3\lambda=-10+16 \\ \text{or,}~~ \lambda=\frac 63=2~~\text{(ans.)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-143cc8da02b2bd8bab3bfa424789b191_l3.png)
![]() If the vectors
If the vectors ![]() and
and ![]() be coplanar, show that
be coplanar, show that ![]()
Solution.
let ![]()
If ![]() are coplanar, then
are coplanar, then

![]() Let
Let ![]() and
and ![]() then, if
then, if ![]() and
and ![]() find
find ![]() which makes
which makes ![]() and
and ![]() coplanar.
coplanar.
Solution.
Since ![]() are coplanar, then
are coplanar, then

![]() Find
Find ![]() such that the four points
such that the four points ![]() and
and ![]() are coplanar.
are coplanar.
Solution.
let ![]()
If the four points ![]() are coplanar,
are coplanar, ![]() are coplanar.
are coplanar.
