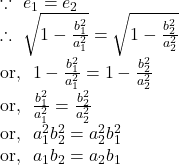In this article, we will do complete solutions of Very Short Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11.

![]() Find the length of the latus rectum and the co-ordinate of the foci of the ellipse
Find the length of the latus rectum and the co-ordinate of the foci of the ellipse ![]()
Solution.
The given equation of ellipse can be written as
![]()
Comparing ![]() with
with ![]() we get
we get
![]()
The length of the latus rectum is
![]()
Now, eccentricity of the ellipse
![]()
The co-ordinates of foci are
![]()
![]() Find the length of the latus rectum of the ellipse
Find the length of the latus rectum of the ellipse ![]()
Solution.
We have, the given equation of ellipse ![]()
Comparing ![]() with
with ![]() we get,
we get,
![]()
So, the length of the latus rectum is given by
![]()
![]() Calculate the eccentricity of the ellipse
Calculate the eccentricity of the ellipse ![]()
Solution.
Comparing the given ellipse with ![]() we get,
we get, ![]()
So, the eccentricity of the ellipse is given by

![]() Find the equations of the directrices of the ellipse
Find the equations of the directrices of the ellipse ![]()
Solution.
The given equation of the ellipse can be written as
![]()
Comparing ![]() with
with ![]() we get,
we get, ![]()
![]()
So, the equations of the directrices of the given ellipse are
![]()
![]() Find the distance between the foci of the ellipse
Find the distance between the foci of the ellipse ![]()
Solution.
The equation of the ellipse can be written as ![]()
Comparing ![]() with
with ![]() we get,
we get, ![]()
Now, the eccentricity ![]() of the ellipse
of the ellipse ![]() is
is
![]()
So, the distance between the foci
![]()
![]() Find the eccentricity of the ellipse if
Find the eccentricity of the ellipse if
![]() the length of the latus rectum is equal to half the minor axis of the ellipse.
the length of the latus rectum is equal to half the minor axis of the ellipse.
Solution.
Let the equation of the ellipse be ![]()
Now, the length of the latus rectum ![]() and the length of the half the minor axis
and the length of the half the minor axis ![]() unit.
unit.
So, by condition,
![]()

![]() the length of the minor axis is equal to half the distance between the foci of the ellipse.
the length of the minor axis is equal to half the distance between the foci of the ellipse.
Solution.
Given :
Minor axis= ![]() (Distance between the foci)
(Distance between the foci)
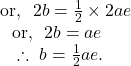
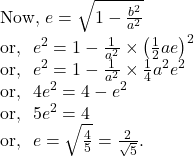
![]() the length of minor axis is equal to the distance between the later recta.
the length of minor axis is equal to the distance between the later recta.
Solution.
We know that the distance between the foci of the ellipse ![]() where
where 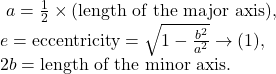
By question,
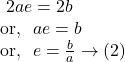
So, by ![]() and
and ![]() we get,
we get,

![]() If the ellipses
If the ellipses ![]() and
and ![]() have same eccentricity, show that
have same eccentricity, show that ![]()
We have the equations of two ellipses which are
![]()
The eccentricity ![]() of
of ![]()
![]()
The eccentricity ![]() of
of ![]()
![]()

![]() The ellipse
The ellipse ![]() has the same eccentricity as the ellipse
has the same eccentricity as the ellipse ![]() . Find the ratio
. Find the ratio ![]()
Solution.
We have the given equation of ellipse ![]()
The eccentricity of ![]()

Again, the eccentricity of ![]() is
is

![]() Find the positions of the points
Find the positions of the points ![]() and
and ![]() with respect to the ellipse
with respect to the ellipse ![]()
Solution.
The equation of the ellipse can be written as ![]()
Case-1 :
![]()
So, the point ![]() lies inside the ellipse.
lies inside the ellipse.
Case-2:
![]()
So, the point ![]() lies on the ellipse.
lies on the ellipse.
Case-3:
![]()
So, the point ![]() lies outside the ellipse.
lies outside the ellipse.
![]() For what values of
For what values of ![]() does the point
does the point ![]() lie outside the ellipse
lie outside the ellipse ![]()
![]() The co-ordinates of a point on the ellipse
The co-ordinates of a point on the ellipse ![]() are
are ![]() ; find the eccentric angle of the point.
; find the eccentric angle of the point.
Solution.
The equation of the given ellipse can be written in standard form as
![]()
Any point on ![]() can be taken as
can be taken as ![]()
Now, by question, we can have
![]()
![]()
Hence, the eccentric angle of the point is ![]()
![]() Find the co-ordinates of the point on the ellipse
Find the co-ordinates of the point on the ellipse ![]() whose eccentric angle is
whose eccentric angle is ![]()
Solution.
The equation of the ellipse can be written as ![]()
Comparing ![]() with the general equation of the ellipse
with the general equation of the ellipse ![]() we get,
we get, ![]()
So, any point on the given ellipse with the eccentric angle ![]() can be written as
can be written as
![]()
So, the co-ordinates of the point on the ellipse ![]() whose eccentric angle is
whose eccentric angle is ![]() is given by
is given by ![]()
![]() If the ellipse
If the ellipse ![]() prove that
prove that ![]()
Solution.
We have the equations of two ellipses which are
![]()
The eccentricity ![]() of
of ![]()
![]()
The eccentricity ![]() of
of ![]()
![]()