In the previous articles , we have done complete solution of Ellipse chapter of S.N.Dey mathematics, Class 11. In this article , we will solve few questions of Hyperbola related problems.

1.Explain what general diagrams are represented by the equation ![]() where
where ![]() and
and ![]() are constants.
are constants.
Solution.
We have the equation given by
![]()
Now, there can be three conditions for different values of ![]()
![]()
Case ![]()
For ![]()
In this case, we get from ![]()

Clearly, ![]() represents the equation of the ellipse.
represents the equation of the ellipse.
Case ![]()
For ![]() we get by
we get by ![]()
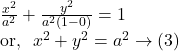
Equation ![]() represents a ‘circle.’
represents a ‘circle.’
Case ![]()
For ![]()
Let ![]()
So, from ![]() we get,
we get,
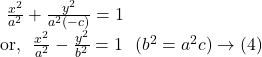
Equation ![]() represents a ‘hyperbola.’
represents a ‘hyperbola.’
2. Show that the eccentricity of any rectangular hyperbola is ![]()
Solution.
We know that the general form of hyperbola is ![]()
The eccentricity ![]() of
of ![]() is given by
is given by
![]()
For rectangular hyperbola, ![]() and so from
and so from ![]() we get,
we get,
![]()
3. Find the eccentricity, co-ordinates of the foci and the equations of the directrices of the hyperbolas :
![]()
Solution.(i)
![]()
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
![]()
![]()
Co-ordinates of foci : ![]()
The equations of directrices of the hyperbola :
![]()
Solution(ii)
![]()
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
![]()
![]()
Co-ordinates of foci : ![]()
The equations of directrices of the hyperbola :

4. Show that the eccentricities of the two hyperbolas ![]() and
and ![]() are equal.
are equal.
Solution.
We have two hyperbolas given by
![]() and
and ![]() .
.
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
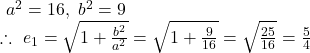
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
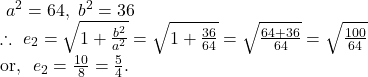
![]()
Note[*] : ![]() eccentricity of the first hyperbola,
eccentricity of the first hyperbola, ![]() eccentricity of the second hyperbola.
eccentricity of the second hyperbola.
![]() Find the co-ordinates of the foci of the hyperbola
Find the co-ordinates of the foci of the hyperbola ![]()
Solution.
![]()
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
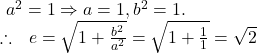
The co-ordinates of foci of the hyperbola ![]() :
:
![]()
![]() Find the eccentricity and the length of latus rectum of the hyperbola
Find the eccentricity and the length of latus rectum of the hyperbola ![]()
Solution.
![]()
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
![]()
So, ![]()
The length of the latus rectum is
![]()
6. Find the length of latus rectum and the equations of the directrices of the hyperbola ![]()
Solution.
![]()
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() , we get
, we get
![]()
The length of the latus rectum of the hyperbola ![]() is
is
![]()
Equations of the directrices of the hyperbola ![]()

7. What type of conic is represented by the equation ![]() What is its eccentricity?
What is its eccentricity?
Solution.
The given equation represents the equation of rectangular hyperbola and its eccentricity is ![]()
8. If the length of conjugate axis and the length of latus rectum of a hyperbola are equal, find its eccentricity.
Solution.
The length of the conjugate axis ![]() unit and the length of the latus rectum is
unit and the length of the latus rectum is ![]() unit of the hyperbola
unit of the hyperbola ![]()
By question,
