In this article, we have solved 6 Long answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Find the equation of the parabola whose vertex is
Find the equation of the parabola whose vertex is ![]() and the equation of latus rectum is
and the equation of latus rectum is ![]() Find the co-ordinates of the point of intersection of this parabola with its latus rectum.
Find the co-ordinates of the point of intersection of this parabola with its latus rectum.
Solution.

The equation of the straight line passing through the point ![]() and perpendicular to
and perpendicular to ![]() is
is ![]()
So, the co-ordinates of the focus of the parabola are ![]()
![]()
So, the required equation of parabola is ![]()
Now, the co-ordinates of the point of intersection of the parabola with its latus rectum are given by ![]() and
and ![]()
![]() The co-ordinates of the two ends of latus rectum of a parabola are
The co-ordinates of the two ends of latus rectum of a parabola are ![]() and
and ![]() find the equation of the parabola.
find the equation of the parabola.
Solution.
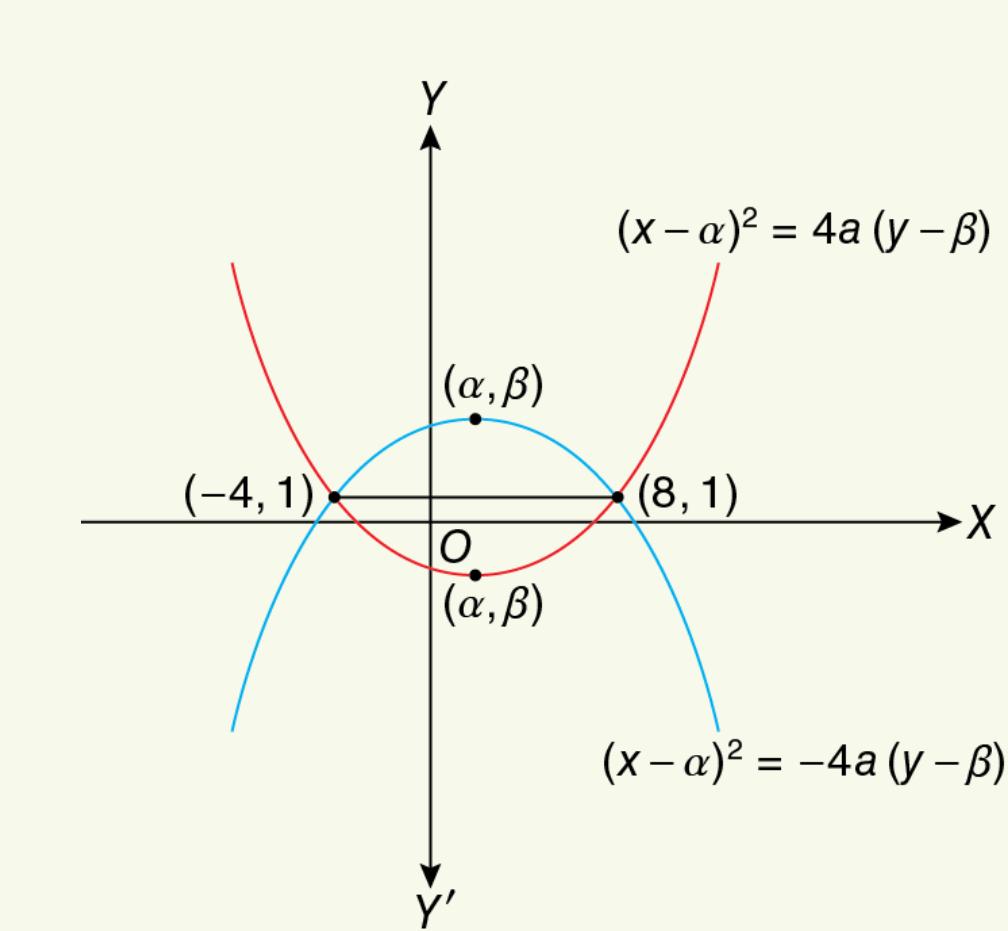
Since the ordinates of the extremities of the latus rectum are equal, so the latus rectum is parallel to ![]() axis and the axis of the parabola is parallel to the
axis and the axis of the parabola is parallel to the ![]() axis.
axis.
So, the equation of latus rectum is ![]() and co-ordinates of focus are given by the mid-point of
and co-ordinates of focus are given by the mid-point of ![]() and
and ![]() which are
which are ![]()
Let the axis of the parabola be ![]() which passes through
which passes through ![]() So, the axis of the parabola is
So, the axis of the parabola is ![]()

The co-ordinates of the vertex of parabola can be ![]() and another possible co-ordinates of the vertex of the parabola can be
and another possible co-ordinates of the vertex of the parabola can be ![]()
So, the equation of the parabola with vertex ![]() is
is

Again, the equation of the parabola with vertex ![]() is
is

![]() Find the equation of the parabola whose vertex is
Find the equation of the parabola whose vertex is ![]() and focus is
and focus is ![]()
Solution.

The equation of the axis of the parabola is the straight line joining the points ![]() and
and ![]() and is given by
and is given by

The equation of the directrix which is perpendicular to the straight line ![]() is
is ![]()
Now, the co-ordinates of the focus ![]() the co-ordinates of the vertex
the co-ordinates of the vertex ![]()
Let the point of intersection of the axis of the parabola and the directrix be ![]()
Since ![]() is the mid-point of
is the mid-point of ![]() and
and ![]() , so
, so
![]()
![]()
Since the straight line ![]() passes through
passes through ![]()
![]()
Hence by ![]() we get the equation of the directrix
we get the equation of the directrix ![]()
Let ![]() be any point on the parabola.
be any point on the parabola.

Since ![]() lies on the required parabola, hence we must have
lies on the required parabola, hence we must have
![Rendered by QuickLaTeX.com ~\overline{SP}=\overline{PM} \\ \text{or,}~~ SP^2=PM^2 \\ \text{or,}~~ (x+6)^2+(y+6)^2=\frac 15 (x+2y-22)^2 \\ \text{or,}~~ 5[(x+6)^2+(y+6)^2]=(x+2y-22)^2\rightarrow(3)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-cdc1d808d3f831f73adab460155cdbfd_l3.png)
Hence, ![]() represents the required equation of parabola.
represents the required equation of parabola.
![]() The directrix of a parabola is
The directrix of a parabola is ![]() and vertex is the point
and vertex is the point ![]() Find
Find ![]() the position of focus and
the position of focus and ![]() the equation of the parabola. [Council Sample Question ‘
the equation of the parabola. [Council Sample Question ‘![]() ]
]
Solution.
The equation of the directrix of the parabola is ![]()
The axis of the parabola is perpendicular to the directrix and is passing through the vertex ![]()
The equation of any straight line perpendicular to ![]() can be written as
can be written as ![]()
Since the straight line ![]() is passing through the point
is passing through the point ![]() ,
,
![]()
So, by ![]() we get the equation of the axis of the parabola which is
we get the equation of the axis of the parabola which is ![]()
Solving ![]() and
and ![]() , we get
, we get ![]()
So, the point of intersection of the axis of parabola and the directrix is ![]()
Let ![]() be the focus of the parabola and
be the focus of the parabola and ![]() be the mid-point of
be the mid-point of ![]() and
and ![]()
![]()
So, ![]()
Let ![]() be any point on the parabola and
be any point on the parabola and ![]() is the perpendicular distance from
is the perpendicular distance from ![]() upon the directrix.
upon the directrix.
![Rendered by QuickLaTeX.com \therefore~\overline{SP}=\overline{PM} \\ \text{or,}~~ SP^2=PM^2 \\ \text{or,}~~ x^2+y^2=\left[\frac{x+y+4}{\sqrt{1^2+1^2}}\right]^2 \\ \text{or,}~~ 2(x^2+y^2)=(x+y+4)^2 \\ \text{or,}~~ x^2+y^2-2xy-8x-8y-16=0\rightarrow(4).](https://examhoop.com/wp-content/ql-cache/quicklatex.com-6bd6daeec14a074ef6eb2f2e5a22dc03_l3.png)
The equation ![]() represents the required parabola.
represents the required parabola.
![]() The axis of a parabola is parallel to
The axis of a parabola is parallel to ![]() axis and it passes through the points
axis and it passes through the points ![]() find its equation.
find its equation.
Solution.
Since the axis of the parabola is parallel to ![]() axis, the equation of the parabola can be written as
axis, the equation of the parabola can be written as ![]()
Since the parabola ![]() is passing through
is passing through ![]()
![]()
Now, the parabola ![]() is passing through the points
is passing through the points ![]() and
and ![]()
![]()

From ![]() and
and ![]() we get,
we get,
![]()
![]()
Hence, the equation of the required parabola is ![]()
![]() A parabola passes through the points
A parabola passes through the points ![]() and its axis is parallel to
and its axis is parallel to ![]() axis. Find its equation.
axis. Find its equation.
Solution.
By the question, since the axis of the parabola is parallel to ![]() axis , the equation of the parabola can be written as
axis , the equation of the parabola can be written as ![]()
Since the parabola ![]() passes through the point
passes through the point ![]() ,
,
![]()
So, equation ![]() can be written as
can be written as ![]()
Since the parabola ![]() passes through the points
passes through the points ![]() and
and ![]()
![]()

From ![]() and
and ![]() we get
we get
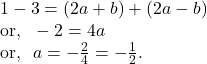
So, ![]()
Hence, the equation of the parabola is

![]() If the extremities of a focal chord of the parabola
If the extremities of a focal chord of the parabola ![]() be
be ![]() and
and ![]() , prove that
, prove that ![]()
Solution.
The equation of the focal chord joining the points ![]() and
and ![]() is
is

Since the focal chord ![]() passes through the point
passes through the point ![]()

![]() If
If ![]() be the co-ordinates of an extremity of a focal chord of the parabola
be the co-ordinates of an extremity of a focal chord of the parabola ![]() the show that the length of the chord is
the show that the length of the chord is ![]()
Solution.
If ![]() be the co-ordinates of an extremity of a focal chord of the parabola, another extremity is
be the co-ordinates of an extremity of a focal chord of the parabola, another extremity is ![]()
So, the length of the chord is
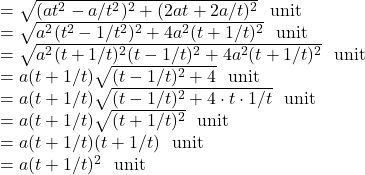
![]() Show that the equation of the chord of the parabola
Show that the equation of the chord of the parabola ![]() through the points
through the points ![]() and
and ![]() on it is
on it is ![]()
Solution.
Since the points ![]() and
and ![]() lie on the parabola
lie on the parabola ![]() so
so
![]()
From ![]() and
and ![]() we get,
we get,

The equation of the straight line joining the points ![]() and
and ![]() is
is
![Rendered by QuickLaTeX.com \frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2} \\ \text{or,}~~ \frac{y-y_1}{x-x_1}=\frac{4a}{y_1+y_2}~~[\text{By (3)}] \\ \text{or,}~~ (y_1+y_2)y-(y_1+y_2)y_1=4a(x-x_1) \\ \text{or,}~~ y^2-(y_1+y_2)y+y_1y_2+y_1^2=4ax_1-4ax+y^2 \\ \text{or,}~~ (y-y_1)(y-y_2)=y^2-4ax ~~[\text{By (1)}]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-f0d1d15f47d3844dc60f45643cd5618e_l3.png)