In the previous article , we have solved 6 Long Answer Type Questions of Parabola Chapter. In this article, we have solved 6 more Long answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Show that the product of the ordinates of the ends of a focal chord of the parabola
Show that the product of the ordinates of the ends of a focal chord of the parabola ![]() is constant.
is constant.
Solution.
We know that the co-ordinates of extremities of the focal chord are ![]() and
and ![]()
So, the product of the ordinates
![]()
![]() If a straight line passing through the focus of the parabola
If a straight line passing through the focus of the parabola ![]() intersects the parabola at the points
intersects the parabola at the points ![]() and
and ![]() then prove that,
then prove that, ![]()
Solution.
Let ![]()
Since the chord of the given parabola passes through the focus ![]() i.e., the chord is the focal chord.
i.e., the chord is the focal chord.
So, ![]()
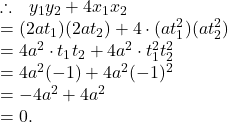
![]() Find the equation of the circle passing through the origin and the foci of the parabolas
Find the equation of the circle passing through the origin and the foci of the parabolas ![]() and
and ![]()
Solution.
The given equations of parabolas are
![]()
The focus of the parabola ![]() is
is ![]() and that of
and that of ![]() is
is ![]()
Let the equation of the circle be
![]()
Since the circle ![]() passes through the points
passes through the points ![]() , so
, so

Hence, the equation of the required circle is
![]()
![]() Find the equation of the circle on
Find the equation of the circle on ![]() as diameter, where
as diameter, where ![]() is the focus of
is the focus of ![]() and
and ![]() is the centre of
is the centre of ![]() Also find the length of the chord of the circle lying along the
Also find the length of the chord of the circle lying along the ![]() axis.
axis.
Solution.
The co-ordinates of the focus ![]() of the parabola
of the parabola ![]() are
are ![]()
The centre ![]() of the given circle
of the given circle ![]() is
is ![]()
Now, the equation of the circle having diameter with extremities ![]() and
and ![]() is
is
![]()
So, the length of the chord of the circle lying along the ![]() axis is
axis is
![]()
![]() is any point on the parabola
is any point on the parabola ![]() is the ordinate of
is the ordinate of ![]() and
and ![]() is the mid-point of
is the mid-point of ![]() Prove that the locus of
Prove that the locus of ![]() is a parabola whose latus rectum is one-fourth that of the given parabola.
is a parabola whose latus rectum is one-fourth that of the given parabola.
Solution.

Let ![]() be any point on the parabola
be any point on the parabola ![]()
Since ![]() is the ordinate of
is the ordinate of ![]()
Also, let ![]() where
where ![]() is the mid-point of
is the mid-point of ![]()
![]()
From ![]() we get
we get
![]()
The locus of ![]() is
is ![]() which represents the equation of a parabola.
which represents the equation of a parabola.
The length of the latus rectum ![]() One-fourth the length of the given parabola.
One-fourth the length of the given parabola.
![]() Find the equation of the circle drawn on the line-segment joining the foci of the two parabolas
Find the equation of the circle drawn on the line-segment joining the foci of the two parabolas ![]() and
and ![]() as diameter.
as diameter.
Solution.
The focus ![]() of the parabola
of the parabola ![]() is
is ![]() and the focus
and the focus ![]() of the parabola
of the parabola ![]() is
is ![]()
Now the equation of the circle drawn on the line-segment joining the foci ![]() and
and ![]() is
is
![]()