In the previous article , we have solved 6 Long Answer Type Questions (7-12) of Parabola Chapter. In this article, we have solved 6 more Long answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

 is a double ordinate of the parabola
is a double ordinate of the parabola 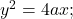 find the equation to the locus of its point of trisection.
find the equation to the locus of its point of trisection.
Solution.

Since ![]() is a double ordinate of the parabola
is a double ordinate of the parabola ![]() let
let ![]()
Let the chord ![]() is trisected at the points
is trisected at the points ![]() and
and ![]() , where
, where ![]()

So, by ![]() we get,
we get,
![]()
Hence, the equation of the required locus of the point of trisection is ![]()
![]() Show that the circle described on a focal chord of a parabola as diameter touches its directrix.
Show that the circle described on a focal chord of a parabola as diameter touches its directrix.
Solution.
Let the equation of the parabola be ![]()
We know the extremities of the focal chord of the parabola ![]() be
be ![]() and
and ![]() .
.
![]() the equation of the circle having diameter as the focal chord with the aforesaid extremities is
the equation of the circle having diameter as the focal chord with the aforesaid extremities is
![]()
Now, the equation of the directrix of the parabola is ![]()
From ![]() and
and ![]() we get,
we get,

So, the point of intersection of the straight line ![]() and the circle
and the circle ![]() is
is ![]()
Since ![]() has only one value, so we can say that the circle touches its directrix.
has only one value, so we can say that the circle touches its directrix.
![]() Prove that the sum of the reciprocals of the segments of any focal chord of a parabola is constant.
Prove that the sum of the reciprocals of the segments of any focal chord of a parabola is constant.
Solution.
Let the equation of the parabola be ![]() and
and ![]() be the focal chord of the parabola.
be the focal chord of the parabola.

![Rendered by QuickLaTeX.com ~l'=\text{distance between the focus}~(a,0)~\text{and}~P'(at_1^2,2at_1)\\=a(t_1^2+1)\\=a\left(\frac{1}{t^2}+1\right)~~[\because~ tt_1=-1]\\=a \left(\frac{t^2+1}{t^2}\right)\\~~\\~\therefore~~\frac 1l+\frac{1}{l'}\\=\frac{1}{a(t^2+1)}+\frac{t^2}{a(t^2+1)}\\=\frac{1+t^2}{a(t^2+1)}\\=\frac 1a=\text{constant}.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-86dd05da6a26e0865a2d194a6a969894_l3.png)
![]() The length of latus rectum of a parabola is
The length of latus rectum of a parabola is ![]() unit. The distance of a point
unit. The distance of a point ![]() on the parabola from its axis is
on the parabola from its axis is ![]() unit. Find the distance of
unit. Find the distance of ![]() from the focus of the parabola.
from the focus of the parabola.
Solution.
Let the equation of the parabola : ![]()
The length of the latus rectum , ![]()
Any point on the parabola can be written as ![]()
By question, ![]()
![]()
![]() The distance between the focus
The distance between the focus ![]() and
and ![]()
![]()
![]() Prove that the length of any chord of the parabola
Prove that the length of any chord of the parabola ![]() passing through the vertex and making an angle
passing through the vertex and making an angle ![]() with the positive direction of the
with the positive direction of the ![]() axis is
axis is ![]()
Solution.
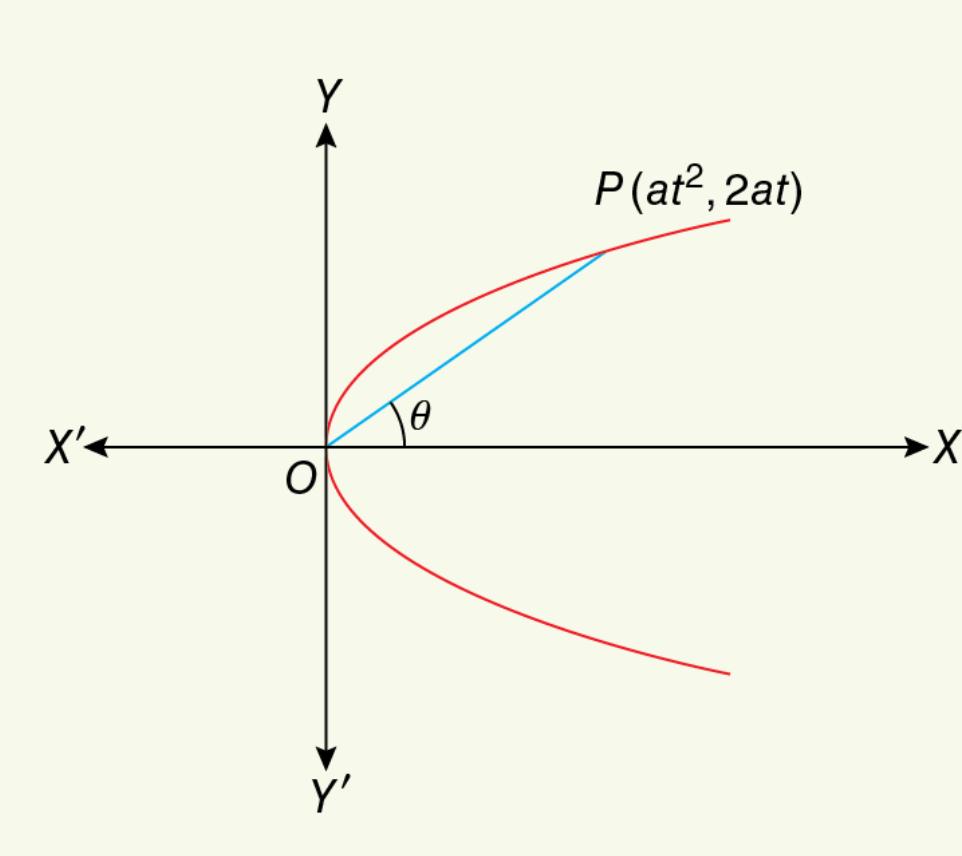
Let ![]() be the chord passing through the vertex
be the chord passing through the vertex ![]() where
where ![]()
By question, the slope of ![]()
![]()
![]() the length of the chord
the length of the chord ![]()
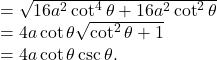
Here, ![]()
![]() If
If ![]() and the line
and the line ![]() is passing through the points of intersection of parabolas
is passing through the points of intersection of parabolas ![]() and
and ![]() then prove that
then prove that ![]() .
.
Solution.
The points of intersection of the parabolas ![]() and
and ![]() are
are ![]() and
and ![]()
Now, if the straight line ![]() passes through the point
passes through the point ![]() , then
, then ![]() which is impossible as
which is impossible as ![]()
So, the straight line ![]() passes through the point
passes through the point ![]() .
.
