In the previous article, we have solved few Short answer type questions of Parabola Chapter . In this article, we have solved Short answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Find the equation of the parabola whose vertex is at
Find the equation of the parabola whose vertex is at ![]() , axis is parallel to
, axis is parallel to ![]() axis and length of the latus rectum is
axis and length of the latus rectum is ![]()
Solution.
We know that the equation of the parabola with the vertex ![]() can be written as
can be written as ![]() where
where ![]() is the length of the latus rectum and the axis of the parabola is parallel to
is the length of the latus rectum and the axis of the parabola is parallel to ![]() axis.
axis.
Here, ![]()
Hence, the required equation of the parabola is
![]()
![]() The co-ordinates of the vertex and focus of a parabola are
The co-ordinates of the vertex and focus of a parabola are ![]() and
and ![]() respectively; find its equation.
respectively; find its equation.
Solution.
![]()
Here, Vertex ![]() . Clearly the focus and vertex of the parabola lie on
. Clearly the focus and vertex of the parabola lie on ![]() which is parallel to
which is parallel to ![]() axis.
axis.
Since the focus lies on the left side of the vertex, the equation of the parabola is ![]()
Here, ![]()
So, the required equation of the parabola is
![]()
![]() Show that the equation of the parabola whose vertex is
Show that the equation of the parabola whose vertex is ![]() and focus is
and focus is ![]() is
is ![]()
Solution.
![]()
Here, Vertex ![]() . Clearly the focus and vertex of the parabola lie on
. Clearly the focus and vertex of the parabola lie on ![]() which is parallel to
which is parallel to ![]() axis.
axis.
Since the focus lies below the vertex, the equation of the parabola is ![]()
Here, ![]()
So, the required equation of the parabola is
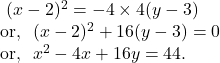
![]() Show that the equation of the parabola whose vertex and focus are on the
Show that the equation of the parabola whose vertex and focus are on the ![]() axis at distances
axis at distances ![]() and
and ![]() from the origin respectively is
from the origin respectively is ![]()
Solution.
Clearly, the vertex of the parabola ![]() Again, the vertex and focus of the parabola lie on the
Again, the vertex and focus of the parabola lie on the ![]() axis . So, the axis of the parabola lies along the
axis . So, the axis of the parabola lies along the ![]() axis.
axis.
Now, the equation of the parabola can be written as
![]() where
where ![]() is the length of the latus rectum.
is the length of the latus rectum.
By question, ![]()
So, by ![]() and
and ![]() we can write the equation of the parabola as
we can write the equation of the parabola as ![]()
Now, ![]()
![]()
Case-1 :

Now, if ![]() , focus lies on the left side of the vertex of the parabola.
, focus lies on the left side of the vertex of the parabola.
![]() the equation of the parabola
the equation of the parabola
![Rendered by QuickLaTeX.com ~y^2=-4|a-a'|(x-a) \\ \text{or,}~~y^2=-4(a-a')(x-a)~\\~~[\because ~a'<a \Rightarrow |a-a'|=a-a'.] \\ \therefore~~y^2=4(a'-a)(x-a).](https://examhoop.com/wp-content/ql-cache/quicklatex.com-db86f6592813f0129e64088014ba8147_l3.png)
Case-2 :
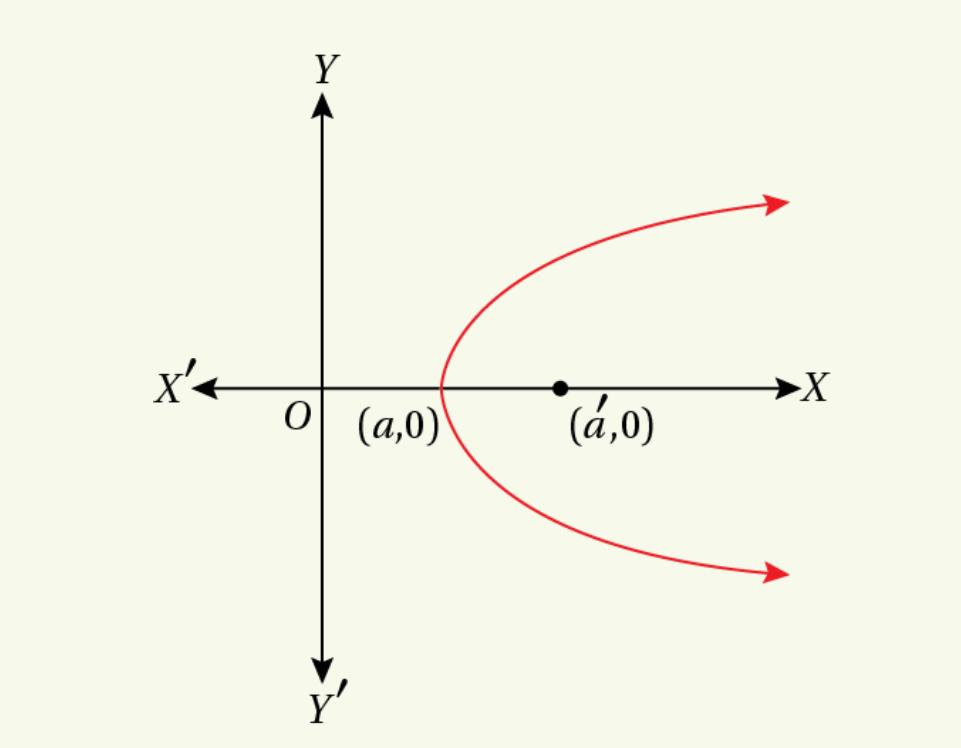
Again, for ![]() , focus lies on the right side of the vertex of the parabola.
, focus lies on the right side of the vertex of the parabola.
![Rendered by QuickLaTeX.com ~y^2=4|a-a'|(x-a) \\ \text{or,}~~y^2=-4(a-a')(x-a)\\~~[\because ~a'>a \Rightarrow |a-a'|=-(a-a').] \\ \therefore~~y^2=4(a'-a)(x-a).](https://examhoop.com/wp-content/ql-cache/quicklatex.com-8378f3747f24511723ddbcbe90242f79_l3.png)
Hence, for both cases, the equation of the parabola is ![]()
![]() Find the equation of the parabola whose vertex is the point
Find the equation of the parabola whose vertex is the point ![]() and directrix is the line
and directrix is the line ![]()
Solution.
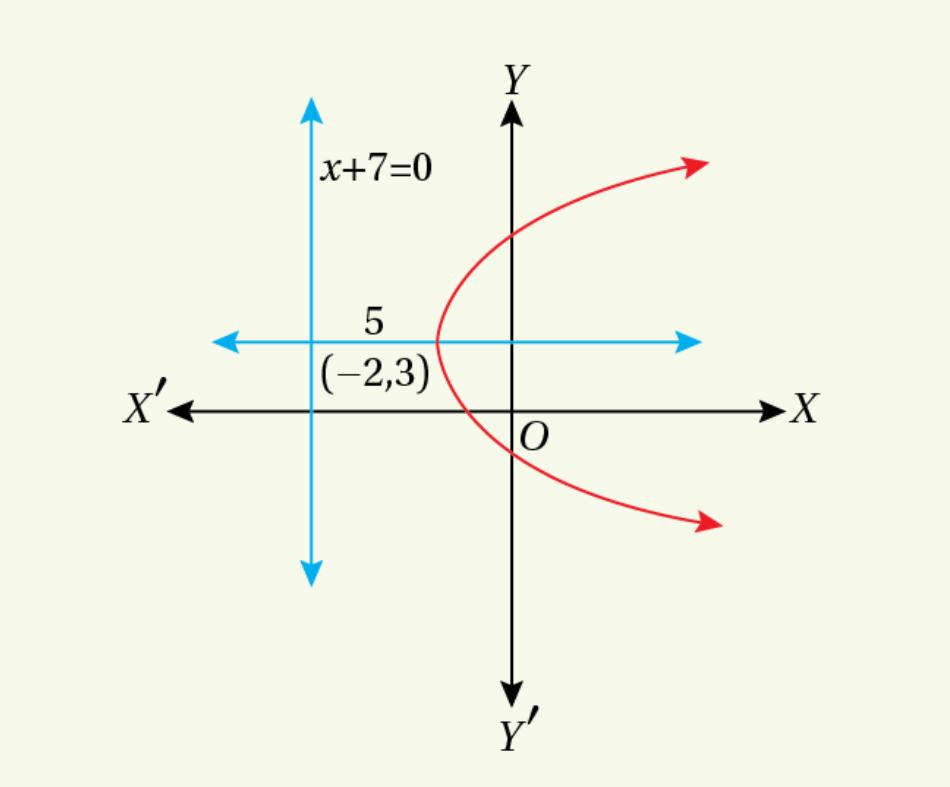
The directrix of the parabola is the line ![]() which is parallel to the
which is parallel to the ![]() axis. So, the axis of the parabola is parallel to
axis. So, the axis of the parabola is parallel to ![]() axis.
axis.
Again, since the vertex of the parabola is on the right side of the directrix, the equation of the parabola can be written as
![Rendered by QuickLaTeX.com ~(y-\beta)^2=4a(x-\alpha) \\ \text{or,}~~ (y-3)^2=4a(x+2)\\~~[~~\because~~\text{Vertex} (\alpha,\beta)=(-2,3)]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-79c440abfd741d8549860f3939aae221_l3.png)
Now, ![]()
Hence, the equation of the required parabola is
![]()
![]() Find the equation of the parabola whose vertex is the point
Find the equation of the parabola whose vertex is the point ![]() and the equation of directrix is
and the equation of directrix is ![]()
Solution.
The equation of the directrix is ![]() The co-ordinates of the vertex is
The co-ordinates of the vertex is ![]()

So, the equation of the parabola is
![]()