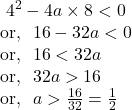In the previous article, we have solved few Short answer type questions (11-15) of Parabola Chapter . In this article, we will solve Very Short answer type questions of Parabola Chapter (Ex-4) of S.N.Dey mathematics, Class 11.

![]() Find the focus , the length of the latus rectum and the directrix of the parabola
Find the focus , the length of the latus rectum and the directrix of the parabola ![]()
Solution.
The given parabola can be written as ![]()
Comparing the parabola ![]() with
with ![]() we get,
we get,
Focus : ![]()
Length of the latus rectum ![]()
The directrix of the parabola :

![]() Find the length of the latus rectum of the parabola
Find the length of the latus rectum of the parabola ![]()
Solution.
The given equation of the parabola can be written as
![Rendered by QuickLaTeX.com ~y=-2x^2+12x-17 \\ \text{or,}~~ y=-2\left(x^2-6x+\frac{17}{2}\right) \\ \text{or,}~~ y= -2 \left[x^2-2 \cdot x \cdot 3+3^2-9+\frac{17}{2}\right] \\ \text{or,}~~ y= -2 \left[(x-3)^2-\frac 12\right] \\ \text{or,}~~ y= -2(x-3)^2+1 \\ \text{or,}~~ y-1=-2(x-3)^2 \\ \text{or,}~~ (x-3)^2=-\frac 12(y-1) \\ \text{or,}~~ (x-3)^2=-4 \cdot \frac 18 (y-1)\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-37596891e452a53efaa32a8d80f7eee5_l3.png)
Hence, the length of the latus rectum of the parabola ![]() is
is
![]()
![]() Find the equation of the parabola whose co-ordinates of the vertex and focus are
Find the equation of the parabola whose co-ordinates of the vertex and focus are ![]() and
and ![]() respectively.
respectively.
Solution.
The given parabola has the vertex ![]() and the focus
and the focus ![]()
Clearly, the axis of the parabola is parallel to the ![]() axis.
axis.
Hence, the equation of the parabola is
![]()
![]() The vertex of a parabola is at the origin and its focus is
The vertex of a parabola is at the origin and its focus is ![]() find the equation of the parabola.
find the equation of the parabola.
Solution.
The given parabola has the vertex ![]() and the focus
and the focus ![]()
Clearly, the axis of the parabola is parallel to the ![]() axis.
axis.
Hence, the equation of the parabola is

![]() The parabola
The parabola ![]() passes through the point
passes through the point ![]() find the co-ordinates of focus and the length of latus rectum.
find the co-ordinates of focus and the length of latus rectum.
Solution.
Since the parabola ![]() passes through the point
passes through the point ![]() we have,
we have,

So, the equation of the parabola turns out to be
![]()
Comparing the parabola ![]() with the parabola
with the parabola ![]() where
where ![]() , we get the focus
, we get the focus ![]() and the length of the latus rectum is given by
and the length of the latus rectum is given by ![]()
![]() The parabola
The parabola ![]() goes through the point of intersection of
goes through the point of intersection of ![]() and
and ![]() Find its focus.
Find its focus.
Solution.
![]()
From ![]() and
and ![]() , we get
, we get

From ![]() we get,
we get,
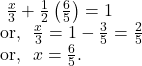
Hence, the point of intersection of ![]() and
and ![]() is
is ![]()
Since the parabola ![]() passes through the point
passes through the point ![]() ,
,

So, the equation of the parabola is
![]()
Hence, the focus of the parabola is ![]()
![]() A parabola having a vertex at the origin and axis along
A parabola having a vertex at the origin and axis along ![]() axis passes through
axis passes through ![]() find the equation of the parabola.
find the equation of the parabola.
Solution.
The equation of the parabola having vertex at ![]() and axis along
and axis along ![]() axis can be written as
axis can be written as
![]()
Since the parabola ![]() is passing through the point
is passing through the point ![]() , so we get by
, so we get by ![]()
![]()
Hence, the equation of the parabola ![]() can be written as
can be written as

![]() Find the equation of the parabola whose vertex is
Find the equation of the parabola whose vertex is ![]() and directrix is the line
and directrix is the line ![]()
Solution.

The equation of the directrix is
![]()
So, the equation of the parabola is along the positive ![]() axis and can be written as
axis and can be written as ![]()
Here, ![]() the distance between the directrix and the vertex of the parabola
the distance between the directrix and the vertex of the parabola ![]() unit.
unit.
![]()
![]() Find the equation of the parabola whose vertex is at the origin and directrix is the line
Find the equation of the parabola whose vertex is at the origin and directrix is the line ![]()
Solution.

The equation of the directrix is ![]()
So, the equation of the directrix is along the negative ![]() axis and can be written as
axis and can be written as ![]() where
where ![]() the distance between the directrix and the vertex of the parabola
the distance between the directrix and the vertex of the parabola ![]() unit.
unit.
![]()
![]() If the parabola
If the parabola ![]() passes through the point of intersection of the straight lines
passes through the point of intersection of the straight lines ![]() and
and ![]() find the co-ordinates of the focus and the length of its latus rectum.
find the co-ordinates of the focus and the length of its latus rectum.
Solution.
![]()
From ![]() , we get
, we get

From 
So, the point of intersection of the given straight lines is ![]()
Since the parabola ![]() passes through the point
passes through the point ![]()
![]()
![]()
So, the co-ordinates of its focus ![]()
The length of its latus rectum is
![]()
![]() The parabola
The parabola ![]() passes through the centre of the circle
passes through the centre of the circle ![]() find the co-ordinates of the focus , length of the latus rectum and the equation of the directrix.
find the co-ordinates of the focus , length of the latus rectum and the equation of the directrix.
Solution.
The equation of the given circle can be written as ![]()
Comparing ![]() with
with ![]() , we get
, we get
![]()
The centre of the given circle is ![]()
Since the given parabola ![]() passes through the point
passes through the point ![]() ,
,
![]()
So, the focus of the parabola ![]()
The length of the latus rectum is
![]()
The equation of the directrix is given by

![]() If the parabola
If the parabola ![]() passes through the centre of the circle
passes through the centre of the circle ![]() what is the length of the latus rectum of the parabola.
what is the length of the latus rectum of the parabola.
Solution.
The equation of the given circle can be written as ![]()
Comparing ![]() with
with ![]() , we get
, we get
![]()
The centre of the given circle is ![]()
Since the given parabola ![]() passes through the point
passes through the point ![]() ,
,
![]()
The length of the latus rectum is
![]()
![]() Find the point on the parabola
Find the point on the parabola ![]() at which the ordinate is double the abscissa.
at which the ordinate is double the abscissa.
Solution.
Let ![]() be a point on the parabola
be a point on the parabola ![]()
By question, ![]()
So, ![]()
Since the point ![]() lies on the given parabola,
lies on the given parabola,
![]()
Hence, ![]()
![]() The point on the parabola
The point on the parabola ![]() at which the ordinate is three times the abscissa.
at which the ordinate is three times the abscissa.
Solution.
Let ![]() be a point on the parabola
be a point on the parabola ![]()
By question, ![]()
So, ![]()
Since the point ![]() lies on the given parabola,
lies on the given parabola,

![]()
![]() Find the point on the parabola
Find the point on the parabola ![]() which forms a triangle of area
which forms a triangle of area ![]() with the vertex and focus of the parabola.
with the vertex and focus of the parabola.
Solution.
Let ![]() be a point on the parabola
be a point on the parabola ![]() . Also, suppose that the vertex
. Also, suppose that the vertex ![]() and the focus
and the focus ![]()
So, area of the triangle ![]()
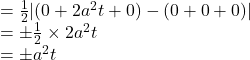
![]()
![]()
![]() What type of conic is the locus of the moving point
What type of conic is the locus of the moving point ![]() Find the equation of the locus.
Find the equation of the locus.
Solution.
Let ![]()
Hence, by ![]() and
and ![]() we get,
we get,

Hence, by ![]() we can conclude that the equation of the conic represents a parabola.
we can conclude that the equation of the conic represents a parabola.
![]() The focal distance of a point on the parabola
The focal distance of a point on the parabola ![]() is
is ![]() find the co-ordinates of the point.
find the co-ordinates of the point.
Solution.
Let the coordinate of that point is ![]()
Equation of the parabola ![]()
Now, the co-ordinates of focus ![]()
By question,
![Rendered by QuickLaTeX.com ~PS=4 \\ \text{or,}~~ \sqrt{(x-2)^2+(y-0)^2}=4 \\ \text{or,}~~ (x-2)^2+y^2=4^2 \\ \text{or,}~~ x^2-4x+4+8x=16~~[\because~y^2=8x] \\ \text{or,}~~ x^2+4x-12=0 \\ \text{or,}~~ x^2+6x-2x-12=0 \\ \text{or,}~~ x(x+6)-2(x+6)=0 \\ \text{or,}~~(x+6)(x-2)=0 \\ \text{or,}~~ x=-6,2.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-69e2875e08dcb71f2d5a23a5e3e3d9de_l3.png)
But since ![]() can not be negative, so
can not be negative, so ![]()
So, ![]()
So, the coordinates are ![]()
![]() Find the focal distance of a point on the parabola
Find the focal distance of a point on the parabola ![]() if the abscissa of the point be
if the abscissa of the point be ![]()
Solution.
The given equation of the parabola is ![]()
So, the focus ![]()
If the abscissa of the point on the given parabola is ![]() then we need to find the ordinate of that point.
then we need to find the ordinate of that point.
![]()
Hence, the focal distance = distance between ![]() and
and ![]()

![]() Determine the positions of the points
Determine the positions of the points ![]() and
and ![]() with respect to the parabola
with respect to the parabola ![]()
Solution.
![]()
![]()
![]()
![]()
From ![]() we can conclude that first point lies outside the parabola, second point lies inside the parabola and third point lies on the given parabola.
we can conclude that first point lies outside the parabola, second point lies inside the parabola and third point lies on the given parabola.
![]() For what values of
For what values of ![]() will the point
will the point ![]() be an inside point of the parabola
be an inside point of the parabola ![]()
Solution.
The given equation of the parabola can be written as ![]() We know if
We know if ![]() lies inside the parabola, then
lies inside the parabola, then ![]()
So, if the point ![]() lies inside the given parabola, then
lies inside the given parabola, then