Plane | Part-3 | Ex-5B Examhoop

In the previous article , we have solved few VSA type questions of Plane Chapter (Ex-2B) of S N De Mathematics(Chhaya). In the following article, we are going to discuss/solve VSA (Very Short Answer) Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Plane (Ex-5B).

8. Find the distance of the point $~(-1, -5, -10)~$ from the point of intersection of the line $~\vec{r}=(2\hat{i}-\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})~$ and the plane $~\vec{r} \cdot (\hat{i}-\hat{j}+\hat{k})=5.$ [NCERT]

Solution.

Let the position vector of the point of intersection be $~(3\lambda+2) \hat{i}+(4\lambda-1)\hat{j}+(2\lambda+2)\hat{k}.$

This point lies on the plane $~\vec{r} \cdot (\hat{i}-\hat{j}+\hat{k})=5.$

$\therefore~~ (3\lambda+2) \times 1+(4\lambda-1) \times (-1)+(2\lambda+2) \times 1=5 \\~~~ \text{or,}~~ 3\lambda+2-4\lambda+1+2\lambda+2=5 \\~~~ \text{or,}~~ \lambda+5=5 \Rightarrow \lambda=0.$

$\therefore~~$ The position vector of the point of intersection is $~(2\hat{i}-\hat{j}+2\hat{k})~~$ i.e. $~(2,-1,2).$

So, the distance between the points $~(2,-1,2)~$ and $~(-1,-5,-10)~$ is

$\sqrt{(2+1)^2+(-1+5)^2+(2+10)^2}=\sqrt{3^2+4^2+12^2}=\sqrt{169}=13~~\text{unit}$

9. Find the value of $~\lambda~$ such that the line $~\frac{x-2}{6}=\frac{y-1}{\lambda}=\frac{z+5}{-4}~$ is perpendicular to the plane $~3x-y-2z=7.$

Solution.

The given straight line is $~~ \frac{x-2}{6}=\frac{y-1}{\lambda}=\frac{z+5}{-4} \longrightarrow (1)~$ and the plane is $~~3x-y-2z=7 \longrightarrow (2)$

Since the straight line (1) is perpendicular to the plane (2),

$\therefore~~ \frac 63=\frac{\lambda}{-1}=\frac{-4}{-2} \\ \text{or,}~~ 2=-\lambda=2 \Rightarrow \lambda =-2~~\text{(ans.)}$

10. Find the distance of the point with position vector $~2\hat{i}+\hat{j}-\hat{k}~$ from the plane $~\vec{r} \cdot (\hat{i}-2\hat{j}+4\hat{k})=9.$

Solution.

The distance of the point $~(2\hat{i}+\hat{j}-\hat{k})~$ from the given plane $~~ \vec{r} \cdot (\hat{i}-2\hat{j}+4\hat{k})-9=0~,$

$=\frac{|(2\hat{i}+\hat{j}-\hat{k}) \cdot (\hat{i}-2\hat{j}+4\hat{k})-9|}{|\hat{i}-2\hat{j}+4\hat{k}|}=\frac{|2-2-4-9|}{\sqrt{1^2+(-2)^2+4^2}}=\frac{|-13|}{\sqrt{1+4+16}}=\frac{13}{\sqrt{21}}~~ \text{unit}$

11. Find the distance between the parallel planes $~\vec{r} \cdot (2\hat{i}-3\hat{j}+6\hat{k})=5~$ and $~\vec{r} \cdot (6\hat{i}-9\hat{j}+18\hat{k})+20=0.$

Solution.

The given planes are $~\vec{r} \cdot (2\hat{i}-3\hat{j}+6\hat{k})=5 \longrightarrow(1)$ and

$~\vec{r} \cdot (6\hat{i}-9\hat{j}+18\hat{k})+20 =0 \\ \text{or,}~~ 3\vec{r} \cdot (2\hat{i}-3\hat{j}+6\hat{k})+20=0 \\ \text{or,}~~ \vec{r} \cdot (2\hat{i}-3\hat{j}+6\hat{k})=-\frac{20}{3} \longrightarrow(2)$

Clearly, the planes (1) and (2) are parallel to each other.

So, the distance between them is

$=\frac{\left|5+\frac{20}{3}\right|}{\sqrt{2^2+(-3)^2+6^2}}=\frac{\left|\frac{35}{3}\right|}{\sqrt{4+9+36}}=\frac{35/3}{7}=\frac 53~~\text{unit.}$

12. If the line $~\vec{r}=(\hat{i}-2\hat{j}+\hat{k})+t(2\hat{i}+\hat{j}+2\hat{k})~$ is parallel to the plane $~\vec{r} \cdot (3\hat{i}-2\hat{j}+m\hat{k})=14~$ , find the value of $~m$ .

Solution.

The given straight line is $~\vec{r}=(\hat{i}-2\hat{j}+\hat{k}) +t(2\hat{i}+\hat{j}+2\hat{k})~~(t \neq 0) \longrightarrow(1)$ and the given plane is $~~\vec{r} \cdot (3\hat{i}-2\hat{j}+m\hat{k})=14 \longrightarrow(2)$

Since the straight line (1) is parallel to the plane (2), so

$~(2\hat{i}+\hat{j}+2\hat{k}) \cdot (3\hat{i}-2\hat{j}+m\hat{k})=0 \\ \text{or,}~~ 6-2+2m=0 \Rightarrow m=-\frac 42=-2.$

13. Find the equation of the plane which contains the line of intersection of the planes $~\vec{r} \cdot (\hat{i}+2\hat{j}+3\hat{k})-4=0~$ and $~\vec{r} \cdot (2\hat{i}+\hat{j}-\hat{k})=0~$ which is perpendicular to the plane $~\vec{r} \cdot (5\hat{i}+3\hat{j}-6\hat{k})+8=0.$

Solution.

$\vec{r} \cdot (\hat{i}+2\hat{j}+3\hat{k})-4=0 \longrightarrow(1),~~\vec{r}\cdot (2\hat{i}+\hat{j}-\hat{k})=0 \longrightarrow(2).$

The equation of the plane which contains the line of intersection of planes (1) and (2) is

$~[\vec{r} \cdot (\hat{i}+2\hat{j}+3\hat{k})-4]+\lambda \vec{r} \cdot (2\hat{i}+\hat{j}-\hat{k})=0 \\ \text{or,}~~ \vec{r} \cdot [(2\lambda+1)\hat{i}+(\lambda+2)\hat{j}+(-\lambda+3)\hat{k}]-4=0 \longrightarrow(3)$

The plane (3) is perpendicular to the plane $~\vec{r} \cdot (5\hat{i}+3\hat{j}-6\hat{k})+8=0.$

$\therefore~~ 5(2\lambda+1)+3(\lambda+2)-6(-\lambda+3)=0 \\ \text{or,}~~ 10\lambda+5+3\lambda+6+6\lambda-18=0 \\ \text{or,}~~ 19\lambda-7=0 \Rightarrow \lambda=\frac{7}{19}.$

Now, we calculate the following values in (3).

$2\lambda+1=2 \times \frac{7}{19}+1=\frac{33}{19},~~ \lambda+2=\frac{7}{19}+2=\frac{45}{19},~~ -\lambda+3=-\frac{7}{19}+3=\frac{50}{19}.$

Hence, from (3) we get,

$~\vec{r} \cdot \left[\frac{33}{19}\hat{i}+\frac{45}{19}\hat{j}+\frac{50}{19}\hat{k}\right]-4=0 \\ \text{or,}~~ \vec{r} \cdot (33\hat{i}+45\hat{j}+50\hat{k})-76=0 \longrightarrow(4)$

So, equation (4) represents the vector equation of the required plane.

14. Find the equation of the plane passing through the points $~(3, 4, 1)~$ and $~(0, 1, 0)~$ and parallel to the line $~\frac{x+3}{2}=\frac{y-3}{7}=\frac{z-2}{5}.$ [CBSE $~~'08$ ]

Solution.

The equation of the plane passing through the point $~(3,4,1)~$ is

$~a(x-3)+b(y-4)+c(z-1)=0 \longrightarrow(1)$

Since the plane (1) is passing through the point $~(0,1,0),$

$~a(0-3)+b(1-4)+c(0-1)=0 \\ \text{or,}~~ -3a-3b-c=0 \Rightarrow 3a+3b+c=0 \longrightarrow(2)$

Since the plane is parallel to the given straight line $~\frac{x+3}{2}=\frac{y-3}{7}=\frac{z-2}{5},$

$\therefore~~ 2a+7b+5c=0 \longrightarrow(3)$

From (2) and (3) we get by cross-multiplication,

$~~\frac{a}{15-7}=\frac{b}{2-15}=\frac{c}{21-6} \Rightarrow \frac a8=\frac{b}{-13}=\frac{c}{15}.$

$\therefore~~$ The required equation of the plane is

$~~8(x-3)-13(y-4)+15(z-1)=0 \\ \text{or,}~~ 8x-24-13y+52+15z-15=0 \\ \text{or,}~~ 8x-13y+15z+13=0~~\text{(ans.)}$

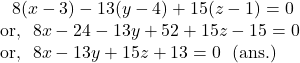
15. Find the coordinates of the point where the line through the points $~A(3, 4, 1)~$ and $~B~(5, 1, 6)~$ crosses the xy-plane.

Solution.

The equation of the any straight line through the points $~A(3,4,1)~$ and $~B(5,1,6)~$ can be written as

$~\frac{x-3}{5-3}=\frac{y-4}{1-4}=\frac{z-1}{6-1} \\ \text{or,}~~ \frac{x-3}{2}=\frac{y-4}{-3}=\frac{z-1}{5}=\lambda (\neq 0,\text{(say)}) \longrightarrow(1)$

So, any point on the straight line (1) can be written as $~~(2\lambda+3,-3\lambda+4,5\lambda+1).$

If this straight line crosses the xy-plane, then $~5\lambda+1=0~$ as on the xy-plane $~~z=0.$

$\therefore~~ \lambda=-\frac 15.$

$\text{Also,}~~ 2\lambda+3=2 \times \left(-\frac 15\right)+3=-\frac 25+3=\frac{-2+15}{5}=\frac{13}{5},\\~~ -3\lambda+4=-3 \times \left(-\frac 15\right)+4=\frac 35+4=\frac{23}{5}.$

$\therefore~~$ The co-ordinates of the point where the line crosses the xy-plane is

$~~(2\lambda+3,-3\lambda+4,0)=\left(\frac{13}{5},\frac{23}{5},0\right).$

Post Views: 222

In the previous article , we have solved few VSA type questions of Plane Chapter (Ex-2B) of S N De Mathematics(Chhaya). In the following article, we are going to discuss/solve VSA (Very Short Answer) Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Plane (Ex-5B).

Leave a Comment Cancel reply