Plane | Part-4 | Ex-5A Examhoop

In the following article, we are going to discuss/solve the last few Very Short Answer Type Questions of the chapter Plane S.N.Dey Mathematics-Class 12 .

Title: Plane in Mathematics: An Essential Concept

Introduction:

In the realm of mathematics, the concept of a plane holds significant importance. A plane is a fundamental geometric object that serves as a foundation for various mathematical principles and applications. Understanding the properties and characteristics of a plane is crucial for solving geometric problems, visualizing three-dimensional objects, and exploring the fascinating world of Euclidean geometry. In this article, we will delve into the basics of planes, their key features, and their applications in mathematics.

Definition and Properties:

A plane is a flat, two-dimensional surface that extends infinitely in all directions. It can be thought of as an imaginary sheet with no thickness. Mathematically, a plane is defined by any three non-collinear points or by a point and two non-parallel vectors. This definition allows for the unique determination of a plane in three-dimensional space.

One of the key properties of a plane is that it is completely determined by any of its parts. This means that if we know three points on a plane or a point on the plane along with two non-parallel vectors, we can precisely define and describe the entire plane.

The concept of a plane also introduces the idea of coplanarity. Three or more points are said to be coplanar if they all lie on the same plane. Coplanar points form the basis for numerous geometrical constructions and proofs.

Intersections and Parallelism:

Planes can intersect with one another in various ways. When two planes intersect, they form a line known as the line of intersection. This intersection can be a single point if the planes are not parallel. However, if the planes are parallel, they never intersect, and the line of intersection is said to be empty.

Parallelism is a significant aspect of planes. Two planes are considered parallel if they do not intersect and have the same orientation. Parallel planes share the same direction, and the distance between them remains constant throughout their extension.

Applications:

The concept of a plane finds applications in numerous branches of mathematics and beyond. In Euclidean geometry, planes play a crucial role in studying the properties of polygons, polyhedra, and other three-dimensional objects. They help us visualize and analyze various geometric figures and their relationships.

Planes are also extensively used in coordinate geometry to represent equations of lines and to solve systems of linear equations. By employing the concept of a plane, mathematicians can model real-world situations and analyze their mathematical properties.

Beyond mathematics, the idea of a plane is applied in fields like computer graphics, architecture, physics, and engineering. Computer-generated images and 3D models rely on planes for rendering and visualization. Architects utilize planes to design buildings and structures, while engineers employ them for analyzing forces and stress distributions in structures.

Conclusion:

The concept of a plane in mathematics is a powerful and versatile tool that provides a basis for understanding geometry, solving equations, and visualizing three-dimensional space. Its properties and applications extend far beyond the realm of mathematics, making it a fundamental concept in various scientific and practical fields. By mastering the fundamentals of planes, mathematicians and professionals alike can navigate complex problems with clarity and precision.

10. Find $~k,~$ for which two planes $~x+ky+5z+2=0~$ and $~3x-2y+kz-1=0$ are perpendicular to one another .

Solution.

The direction ratios of the plane $~x+ky+5z+2=0~$ is given by $~(1,k,5)~$ and the direction ratios of the plane $~3x-2y+kz-1=0~$ is given by $~(3,-2,k).$

Since the planes are perpendicular to one another,

$~ 1 \times 3+ k \times (-2)+ 5 \times k=0 \\ \text{or,}~~ 3-2k+5k=0 \\ \text{or,}~~ 3k=-3 \\ \text{or,}~~ k=\frac{-3}{3}=-1.$

11. A plane meets the coordinate axes at $~L,M,N~$ respectively, such that the centroid of the triangle $~LMN~$ is $~(1,-2,3)$ . Find the equation of the plane.

Solution.

Let $~L \equiv (a,0,0),~ M \equiv (0,b,0),~ N \equiv (0,0,c).$

So, the equation of the plane can be written as

$~\frac xa+\frac yb+\frac zc=1 \rightarrow(1)$

Since the centroid of the $~\Delta LMN~$ is $~(1,-2,3),$

$\text{so,}~~ \frac{a+0+0}{3}=1 \Rightarrow a=3,~~\frac{0+b+0}{3}=-2 \Rightarrow b=-6,~~ \frac{0+0+c}{3}=3 \Rightarrow c=9.$

$\therefore~$ the equation of the plane is $~ \frac x3-\frac y6+\frac z9=1.$

12. Find the equation of the plane which passes through the point $~(2, 1, -1)~$ and is orthogonal to each of the planes $~x-y+z = 1~$ and $~3x+4y-2z = 0.$

Solution.

Since the passes through the point $~(2,1,-1)~$ , the equation of the plane can be written as

$~a(x-2)+b(y-1)+c(z+1)=0 \longrightarrow(1)$

Since the plane $(1)$ is perpendicular to each of the given planes $~x-y+z=1~$ and $~3x+4y-2z=0~$ ,

$a-b+c=0 \rightarrow(2),~~3a+4b-2c=0 \rightarrow(3)$

From $(2)$ and $(3)$ , we get by cross-multiplication

$~\frac{a}{2-4}=\frac{b}{3+2}=\frac{c}{4+3} \\ \text{or,}~~ \frac{a}{-2}=\frac{b}{5}=\frac{c}{7}=\lambda(\neq 0) \\ \therefore~~ a=-2\lambda,~~b=5\lambda,~c=7\lambda.$

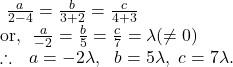
Now, putting the values of $~a,b,c~$ in $(1)$ we get,

$~ -2\lambda(x-2)+5\lambda(y-1)+7\lambda(z+1)=0 \\ \text{or,}~~ -2(x-2)+5(y-1)+7(z+1)=0.$

Disha Objective NCERT Xtract Mathematics for NTA JEE Main 6th Edition One Liner Theory, MCQs on every line of NCERT, Tips on your Fingertips, Previous … Bank, Mock Tests, Useful for BITSAT & VITEEE Paperback

13. Show that the equation of the plane which passes through the point $~(1, 2, 3)~$ and parallel to the plane $~3x+4y-5z=0~$ is $~3x+4y-5z+4=0.$

Solution.

The equation of the plane can be written as

$~a(x-1)+b(y-2)+c(z-3)=0 \longrightarrow(1)$

Since the plane (1) is parallel to the plane $~3x+4y-5z=0~$ , direction ratios of normal to the plane (1) are $~3,4,-5.$

Hence, the equation of the plane (1) is

$~3(x-1)+4(y-2)-5(z-3)=0 \\ \text{or,}~~ 3x-3+4y-8-5z+15=0 \\ \text{or,}~~ 3x+4y-5z+4=0.$

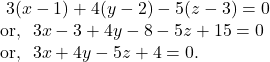
Authentic SHORTCUTS, TIPS, TRICKS & TECHNIQUES in MATHEMATICS for JEE Main, Advanced & KVPY Paperback

14. Prove that the equation of the plane which passes through the point $~(2, -3, 5)~$ and which is parallel to the $yz$ -plane is $~x=2.$

Solution.

Since the plane passes through the point $~(2,-3,5)~$ , the equation of the plane can be written as

$~a(x-2)+b(y+3)+c(z-5)=0 \longrightarrow(1)$

Since the plane (1) is parallel to the plane $~yz,~$ so the direction ratios of the normal to the plane (1) are $~1,0,0.$

So, the equation of the plane (1) is

$~1(x-2)+0(y+3)+0(z-5)=0 \\ \text{or,}~~ x-2=0 \Rightarrow x=2.$

15. Find the equation of the plane which is parallel to the plane $~2x+4y+5z=6~$ and the sum of whose intercepts on the coordinate axes is $~19.$

Solution.

The equation of the plane which is parallel to $~2x+4y+5z=6~$ is

$~2x+4y+5z=k~~(k \neq 0,~\text{constant}) \\ \text{or,}~~ \frac{x}{k/2}+\frac{y}{k/4}+\frac{z}{k/5}=1$

By question, we get

$\frac k2+\frac k4+\frac k5=19 \\ \text{or,}~~ k \left(\frac 12+\frac 14+\frac 15\right)=19 \\ \text{or,}~~ k \times \frac{10+5+4}{20}=19 \\ \text{or,}~~ k \times \frac{19}{20}=19 \Rightarrow k=20.$

Hence, the equation of the plane is $~ 2x+4y+5z=20.$

Post Views: 213

In the following article, we are going to discuss/solve the last few Very Short Answer Type Questions of the chapter Plane S.N.Dey Mathematics-Class 12 .

Title: Plane in Mathematics: An Essential Concept

Leave a Comment Cancel reply