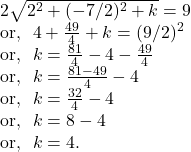Today we are going to discuss the Short Answer Type Questions of Circle of S N Dey mathematics Class 11.

S N Dey Math Solutions related to Circle (Ex -3)
![]() Examine whether the equation
Examine whether the equation ![]() represents a circle.
represents a circle.
Solution.
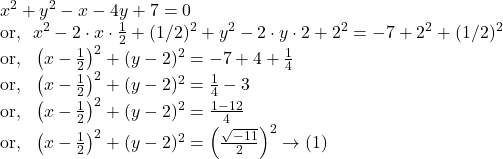
Hence, by ![]() we notice that the radius of the circle being a imaginary number and so, the given equation does not represent a real circle.
we notice that the radius of the circle being a imaginary number and so, the given equation does not represent a real circle.
![]() Find the equation of the circle passing through
Find the equation of the circle passing through ![]() and having centre at
and having centre at ![]()
Solution.
We know that the general form of equation of the circle is :
![]() where
where ![]() is the centre of the circle given by
is the centre of the circle given by ![]()
![]()
Since the circle passing through ![]() , we get by
, we get by ![]() and
and ![]()
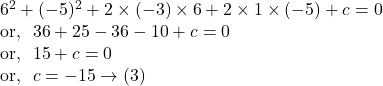
Hence, by ![]() we get, the equation of the circle
we get, the equation of the circle
![]()
![]() Find the centre and radius of each of the following circles :
Find the centre and radius of each of the following circles :
![]()
Solution.
We know that the equation of the circle having centre at ![]() and radius
and radius ![]() unit is
unit is
![]()
Now, ![]() can be written as :
can be written as :
![]()
Hence, from ![]() and
and ![]() , we get, the centre of the given circle is
, we get, the centre of the given circle is ![]() and the radius is
and the radius is ![]() unit.
unit.
![]()
Solution.
![Rendered by QuickLaTeX.com x^2+y^2-3x+2y-19=0 \\ \text{or,}~~ x^2-2 \cdot x \cdot \frac 32+(3/2)^2+y^2+2 \cdot y \cdot 1+1^2\\=19+(3/2)^2+1^2 \\ \text{or,}~~ \left(x-\frac 32\right)^2 +(y+1)^2=20+\frac 94 \\ \text{or,}~~ \left(x-\frac 32\right)^2 +(y+1)^2=\frac{89}{4} \\ \text{or,}~~ \left(x-\frac 32\right)^2 +[y-(-1)]^2 =\left(\frac{\sqrt{89}}{2}\right)^2 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c519cd7ea3a77c5410a1a19bcd20e679_l3.png)
Hence, from ![]() we get, the centre of the given circle is
we get, the centre of the given circle is ![]() and the radius is
and the radius is ![]() unit.
unit.
![]()
Solution.
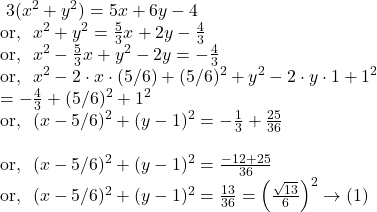
Hence, from ![]() we get, the centre of the given circle is
we get, the centre of the given circle is ![]() and the radius is
and the radius is ![]() unit.
unit.
![]()
Solution.
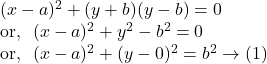
Hence, from ![]() we get, the centre of the given circle is
we get, the centre of the given circle is ![]() and the radius is
and the radius is ![]() unit.
unit.
4. Under what conditions ![]() will be the equation of a circle? In that case what will be the co-ordinates of the centre ?
will be the equation of a circle? In that case what will be the co-ordinates of the centre ?
Solution.
![]() will represent an equation of a circle if
will represent an equation of a circle if
![]()
For ![]() the given equation can be written as follows :
the given equation can be written as follows :
![]()
Comparing the equation ![]() with the general / standard form of circle, we can say that the centre of the circle is :
with the general / standard form of circle, we can say that the centre of the circle is : ![]()
![]() Find the radius of the circle which passes through the origin and the points
Find the radius of the circle which passes through the origin and the points ![]() and
and ![]()
Solution.
The general equation of the circle is given by :
![]()
Since the circle which passes through the origin, we get ![]() ,
, ![]()
So, the equation ![]() can be rewritten as
can be rewritten as
![]()
Since the circle passes through the point ![]() , we get by
, we get by ![]()
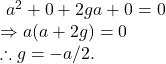
Again, since the circle passes through the point ![]() we get by
we get by ![]()
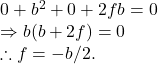
Hence, the radius of the circle as represented by ![]() is given by :
is given by :
![]()
![]() Find the equation of the circle for which the line segment joining the points
Find the equation of the circle for which the line segment joining the points ![]() and
and ![]() and
and ![]() is a diameter.
is a diameter.
Solution.
According to the problem, The mid-point of the line segment joining the points ![]() and
and ![]() will be the centre of the circle and the centre of the circle is :
will be the centre of the circle and the centre of the circle is :
![]()
The diameter of the circle is the length of the line segment joining the points ![]() and
and ![]() and is given by :
and is given by :
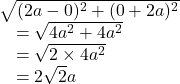
and so, the radius of the circle is :
![]()
Hence, the required equation of the circle is :
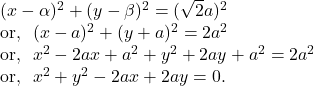
2nd Part :
Solution.
According to the problem, The mid-point of the line segment joining the points ![]() and
and ![]() will be the centre of the circle and the centre of the circle is :
will be the centre of the circle and the centre of the circle is :
![]()
The diameter of the circle is the length of the line segment joining the points ![]() and
and ![]() and is given by :
and is given by :
![]()
and so, the radius of the circle is : ![]()
Hence, the required equation of the circle is :
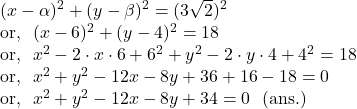
![]() Find the position of the point
Find the position of the point ![]() with respect to the circle whose equation is
with respect to the circle whose equation is ![]()
Solution.
Comparing the given equation of the circle with the general equation / standard form of circle i.e., with ![]() , we get,
, we get,
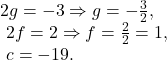
Hence, the radius of the circle is :
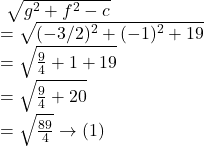
Again, the centre of the circle is given by : ![]()
Now, the distance of the point ![]() from the centre of the circle i.e.,
from the centre of the circle i.e., ![]() is :
is :
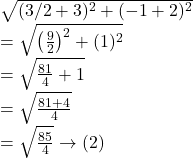
Hence, from ![]() and
and ![]() we get,
we get,
![]() and so, the point
and so, the point ![]() lies inside the given circle.
lies inside the given circle.
![]() The straight line
The straight line ![]() is a tangent to the circle
is a tangent to the circle ![]() at P ; find the equation of its normal at the same point.
at P ; find the equation of its normal at the same point.
Solution.
Given that straight line ![]() is tangent to the circle
is tangent to the circle ![]() .
.
Now, General equation of circle ![]() where center of circle is :
where center of circle is :![]() and radius of circle is :
and radius of circle is : ![]()
Comparing the given equation to general equation we get,
![]()
So, center of circle ![]() .
.
Now, the equation of the straight line which is perpendicular to the given straight line is : ![]() which passes through the point
which passes through the point ![]() and so,
and so,
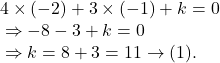
Hence, the equation of its normal at the same point is given by :
![]()
![]() The length of diameter of the circle
The length of diameter of the circle ![]() is
is ![]() find
find ![]()
Solution.
General equation of circle ![]() where center of circle is :
where center of circle is :![]() and radius of circle is :
and radius of circle is : ![]()
Comparing the given equation to general equation we get,

So, center of circle ![]() .
.
The radius of the circle : ![]()
So, according to the given problem,