Circle | Part-2 | S N Dey

by

Circle, S N Dey mathematics Class 11

In the previous article , we discussed 10 Very Short Answer Type Questions. In this article, we will discuss few more VSA type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Circle related Problems and Solutions | S N Dey Mathematics

11. The co-ordinates of the centre of the circle ~2x^2+2y^2+ax+by+c=0~ are ~(3,-4)~; find ~a~ and ~b.

Solution.

The given equation of the circle can be rewritten as :

x^2+y^2+(a/2)x+(b/2)y+c/2=0 \rightarrow(1)

Now, comparing the equation ~(1),~ with the general / standard form of circle ~x^2+y^2+2gx+2fy+c=0, we get,

2g=a/2 \Rightarrow g=a/4, ~2f=b/2 \Rightarrow f=b/4.

So, the centre of the circle as represented by ~(1),~ is :

(-g,-f)=(-a/4,-b/4)=(3,-4) \rightarrow(2)

By (2),~ we get,

~-\frac a4=3 \Rightarrow a=-12,~~-\frac b4=-4 \Rightarrow b=16.

  • To download full PDF solution of Circle ( Chhaya Mathematics, Class 11 ), click here.

12. Find the equation of the circle which touches both the co-ordinate axes at a distance ~+3~ unit from the origin.

Solution.

From the given condition, we can say that the centre of the circle is ~(3,3)~ and the radius of the circle is ~3~ unit so that the equation of the circle can be written as :

(x-3)^2+(y-3)^2=3^2 \\ \text{or,}~~x^2-2 \cdot x \cdot 3+3^2+y^2-2 \cdot y \cdot 3+3^2=9 \\ \text{or,}~~ x^2+y^2-6x-6y+9=0.

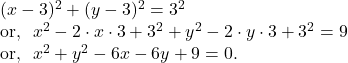
13. Find the parametric equation of the circle ~x^2+y^2+4x-8y-5=0.

Solution.

We have, ~x^2+y^2+4x-8y-5=0\rightarrow(1)

Comparing the equation ~(1),~ with the general / standard form of circle ~x^2+y^2+2gx+2fy+c=0, we get,

2g=4 \Rightarrow g=\frac 42=2, ~~2f=-8 \Rightarrow f=-\frac 82=-4, ~~c=-5.

The centre of the given circle is : (-g,-f)=(-2,4).

The radius of the circle :

\sqrt{g^2+f^2-c}=\sqrt{2^2+(-4)^2+5}=\sqrt{25}=5.

Hence, the equation of the circle is :

[x-(-2)]^2+(y-4)^2=5^2 \\ \text{or,}~~ (x+2)^2+(y-4)^2=5^2 \rightarrow(2)

By (2),~ we get,

x+2=5 \cos\theta \Rightarrow x=-2+5\cos\theta\rightarrow(3), \\~~ y-4=5\sin\theta \Rightarrow y=4+5\sin\theta\rightarrow(4).

The equations ~(3),(4)~ together represent the parametric equation of the circle.

14. The parametric equation of a circle are, ~x=\frac 12(-3+4\cos\theta),~y=\frac 12(1+4\sin\theta).~ Find the equation of the circle.

Solution.

We have,

x=\frac 12(-3+4\cos\theta) =-\frac 32+2\cos\theta \\ \therefore x+\frac 32=2\cos\theta \rightarrow(1)

y=\frac 12(1+4\sin\theta)=\frac 12+2\sin\theta \\ \therefore y-\frac 12=2\sin\theta\rightarrow(2)

Hence, from (1),~(2)~ we get,

(x+3/2)^2+(y-1/2)^2=(2\cos\theta)^2+(2\sin\theta)^2 \\ \text{or,}~~ x^2+2 \cdot x \cdot \frac 32+(3/2)^2+y^2-2 \cdot y \cdot \frac 12+(1/2)^2=4(\cos^2\theta+\sin^2\theta) \\ \text{or,}~~x^2+3x+\frac 94+y^2-y+\frac 14=4 \\ \text{or,}~~ x^2+y^2+3x-y+\left(\frac{9+1}{4}-4\right)=0 \\ \text{or,}~~ x^2+y^2+3x-y -\frac 32=0 \\ \text{or,}~~2x^2+2y^2+6x-2y-3=0.

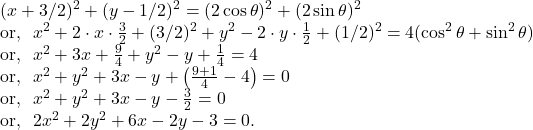
15. The equation of the in-circle of an equilateral triangle is ~x^2+y^2+2x-4y-8=0;~ find the area of the equilateral triangle.

Solution.

The equation of the in-circle of an equilateral triangle is given by ~x^2+y^2+2x-4y-8=0.

Comparing the equation ~(1),~ with the general / standard form of circle ~x^2+y^2+2gx+2fy+c=0, we get,

2g=2 \Rightarrow g=\frac 22=1,~2f=-4 \Rightarrow f=-\frac 42=-2,~c=-8.

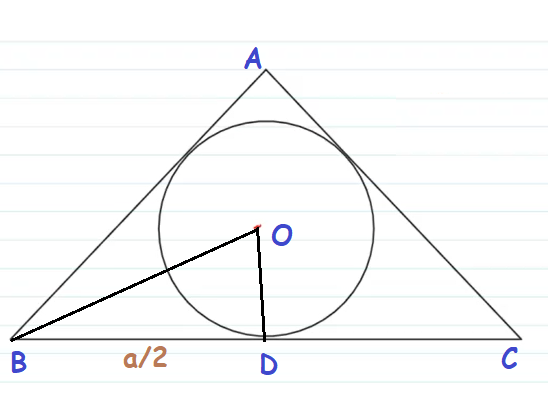
The radius of the circle is :

OD=\sqrt{g^2+f^2-c}=\sqrt{1^2+(-2)^2+8}=\sqrt{1+4+8}=\sqrt{13}.

Clearly, from the figure we notice that \angle {OBD}=30^{\circ}. Now let BC=a~\text{unit}~ so that ~BD=a/2~\text{unit.}

\tan {30^{\circ}}=\frac{OD}{BD}=\frac{OD}{a/2} \\ \text{or,}~~ \frac{1}{\sqrt{3}}=\frac{\sqrt{13}}{a/2} \\ \text{or,}~~ \frac a2=\sqrt{39} \\ \therefore a= 2\sqrt{39}.

Post Views: 214

Leave a Comment