In the previous article, we have discussed the solutions of 10 Long Answer type questions of Integration By Parts Chapter of S N Dey mathematics Class 12. In this chapter, we will discuss few more problems of Long Answer Type Questions.

Integration By Parts | Long Answer Type Questions | S N Dey | Ex-7
![]()
Solution.
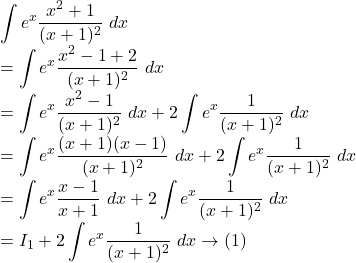
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{e^x\frac{x-1}{x+1}}~dx\\=\frac{x-1}{x+1} \int{e^x}~dx-\int{\left[\frac{d}{dx}\left(\frac{x-1}{x+1}\right) \int{e^x}~dx\right]}~dx \\= \frac{x-1}{x+1} \cdot e^x-\int{ \frac{(x+1) \cdot 1-(x-1) \cdot 1}{(x+1)^2} \cdot e^x}~dx\\=\frac{x-1}{x+1} \cdot e^x-\int{\frac{2}{(x+1)^2} \cdot e^x}~dx\\=\frac{x-1}{x+1} \cdot e^x-2\int{e^x \frac{1}{(x+1)^2}}~dx \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-1fe870ab6e2bbfe93202f1fd27a56674_l3.png)
Hence, from ![]() we get,
we get,
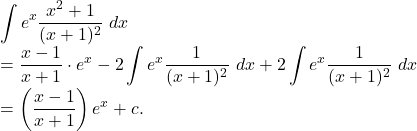
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{e^x\left(\frac{x+2}{x+4}\right)^2}~dx\\=\int{e^x\left(1-\frac{2}{x+4}\right)^2}~dx\\=\int{e^x \left[1-\frac{4}{x+4}+\frac{4}{(x+4)^2}\right]}~dx\\=\int{e^x}~dx-4\int{\frac{e^x}{x+4}}~dx+4\int{\frac{e^x}{(x+4)^2}}~dx\\=e^x-4I_1+4\int{\frac{e^x}{(x+4)^2}}~dx+c \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-e401b6f3256e2fa84055a13abf02843b_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{\frac{e^x}{x+4}}~dx\\=\frac{1}{x+4} \int{e^x}~dx-\int{\left[\frac{d}{dx}\left(\frac{1}{x+4}\right) \int{e^x}~dx\right]}~dx\\=\frac{e^x}{x+4}+\int{\frac{e^x}{(x+4)^2}}~dx\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-df44a907e3d56d1f5d24471064bfc2ec_l3.png)
Hence, by ![]() we get ,
we get ,
![Rendered by QuickLaTeX.com \displaystyle\int{e^x\left(\frac{x+2}{x+4}\right)^2}~dx\\=e^x-4\left[\frac{e^x}{x+4}+\int{\frac{e^x}{(x+4)^2}}~dx\right]+4\int{\frac{e^x}{(x+4)^2}}~dx+c\\=e^x-\frac{4e^x}{x+4}+c\\=\frac{xe^x+4e^x-4e^x}{x+4}+c\\=\frac{xe^x}{x+4}+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-5c38cf72d2e87cc9bf370699e1550db3_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{e^x\sin x}~dx\\=e^x\int{\sin x}~dx- \int{\left[\frac{d}{dx}(e^x) \int{\sin x}~dx\right]}~dx\\=-e^x \cos x-\int{e^x(-\cos x)}~dx\\=-e^x \cos x+\int{e^x\cos x}~dx\\=-e^x \cos x+I_1 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-bea415b305f85a1f06e114bf4c814d11_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{e^x\cos x}~dx\\=e^x \int{\cos x}~dx -\int{\left[\frac{d}{dx}(e^x) \int{\cos x}~dx\right]}~dx\\=e^x\sin x-\int{e^x\sin x}~dx\\=e^x\sin x-I+c_1 \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-8c4d085f867afe06ad0f231a5ce45886_l3.png)
Hence, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com I=-e^x \cos x+e^x\sin x-I +c_1 \\ \therefore~I+I=e^x(-\cos x+\sin x) +c_1 \\ \text{or,}~ 2I=e^x(\sin x-\cos x) +c_1 \\ \text{or,}~ I=\frac 12 e^x(\sin x-\cos x)+c.~~[~c=c_1/2~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-508030f4d4d4ae5a8f1f51a024c798c4_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{e^{3x}\cos4x}~dx\\=e^{3x} \int{\cos4x}~dx-\int{\left[\frac{d}{dx}(e^{3x}) \int{\cos4x}~dx\right]}~dx\\=e^{3x}\left(\frac{\sin4x}{4}\right)-\int{3e^{3x}\cdot \frac{\sin4x}{4}}~dx\\=e^{3x}\left(\frac{\sin4x}{4}\right)-\frac 34\int{e^{3x}\sin4x}~dx\=e^{3x}\left(\frac{\sin4x}{4}\right)-\frac 34I_1\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-9b8fcecbd1f4787f2024722514de74df_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{e^{3x}\sin4x}~dx\\=e^{3x}\int{\sin4x}~dx-\int{\left[\frac{d}{dx}(e^{3x}) \int{\sin4x}~dx\right]}~dx\\=e^{3x}\left(-\frac{\cos4x}{4}\right)-\int{3e^{3x} \cdot\left(-\frac{\cos4x}{4}\right) }~dx\\=e^{3x}\left(-\frac{\cos4x}{4}\right)+\frac 34\displaystyle\int{e^{3x}\cos4x}~dx \\=e^{3x}\left(-\frac{\cos4x}{4}\right)+\frac 34I+c_1\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-d145b0acbab985c4a7657c85a5767f29_l3.png)
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com I=e^{3x}\left(\frac{\sin4x}{4}\right)-\frac 34\left[e^{3x}\left(-\frac{\cos4x}{4}\right)+\frac 34I\right]+c_1\\~~ \\ \text{or,}~~ I=\frac 14e^{3x}\sin4x+\frac{3}{16}e^{3x}\cos4x-\frac{9}{16}I +c_1\\~~ \\ \therefore~ \left(1+\frac{9}{16}\right)I=\frac 14e^{3x}\sin4x+\frac{3}{16}e^{3x}\cos4x +c_1\\~~ \\ \text{or,}~~ \frac{25}{16}I=\frac 14e^{3x}\sin4x+\frac{3}{16}e^{3x}\cos4x+c_1\\~~ \\ \text{or,}~~ 25 I=4e^{3x}\sin4x+3e^{3x}\cos4x+16c_1\\~~ \\ \text{or,}~~ I=\frac{e^{3x}}{25}(4e^{3x}\sin4x+3e^{3x}\cos4x )+c.~~[~c=\frac{16}{25}c.~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-b023c274774334f9fe6bace3b87f22da_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{2^x \sin x}~dx\\=\sin x \int{2^x}~dx- \int{\left[\frac{d}{dx}(2^x) \int{\sin x}~dx\right]}~dx\\=\frac{2^x\sin x}{\log 2}-\int{\cos x \cdot \frac{2^x}{\log 2}}~dx\\=\frac{2^x\sin x}{\log 2}-\frac{1}{\log 2} I_1\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-371c3721c10486edb711c6c5b64ef4db_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{2^x \cos x}~dx\\=\cos x\int{2^x}~dx-\int{\left[\frac{d}{dx}(\cos x) \int{2^x}~dx\right]}~dx\\= \frac{2^x \cos x}{\log 2}- \int{(-\sin x) \cdot \frac{2^x}{\log 2}}~dx\\=\frac{2^x \cos x}{\log 2}+\frac{1}{\log 2} \int{2^x \sin x}~dx\\=\frac{2^x \cos x}{\log 2}+\frac{1}{\log 2}I \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-03caf68142917b637b6070e4861fad29_l3.png)
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com I=\frac{2^x\sin x}{\log 2}-\frac{1}{\log 2}\left[\frac{2^x \cos x}{\log 2}+\frac{1}{\log 2}I \right]\\~~ \\ \text{or,}~~ I+\frac{1}{(\log 2)^2}I=\frac{2^x \sin x}{\log 2}-\frac{2^x \cos x}{(\log 2)^2}\\~~ \\ \text{or,}~~ \left[1+\frac{1}{(\log 2)^2}\right]I=\frac{2^x}{(\log 2)^2}[\sin x \log 2-\cos x]+c_1\\~~ \\ \text{or,}~~ \left[\frac{(\log 2)^2+1}{(\log 2)^2}\right]I=\frac{2^x}{(\log 2)^2}[\sin x \log 2-\cos x]+c_1\\~~ \\ \therefore~ I=\frac{2^x}{(\log 2)^2+1}[\sin x \log 2-\cos x]+c.[*]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-2f80fc3a60bb06bc5065cca10b48e1dd_l3.png)
Note [*] : ![]()
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{3^{2x} \cos2x}~dx\\=\int{e^{\log 3^{2x}}\cos2x}~dx\\=\int{e^{2x \log 3}\cos2x}~dx\\=\int{e^{(2\log 3)x} \cdot \cos2x}~dx\\=\frac{e^{(2\log 3)x}}{(2\log 3)^2+2^2}[(2\log 3)\cos2x+2\sin2x]+c~[*]\\=\frac{e^{(\log 3^2)x}}{(\log 3^2)^2+2^2}[(\log 3^2)\cos2x+2\sin2x]+c\\=\frac{e^{(\log 9)x}}{(\log 9)^2+2^2}[(\log 9)\cos2x+2\sin2x]+c](https://examhoop.com/wp-content/ql-cache/quicklatex.com-65a36d98713b51fdb9301cc6054dd425_l3.png)
Note[*]: ![]()
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{e^x \cos^2x}~dx\\=\frac 12 \displaystyle\int{e^x (2\cos^2x)}~dx\\=\frac12\int{e^x(1+\cos2x)}~dx\\=\frac 12 \int{e^x}~dx+\frac 12\int{e^x \cos2x}~dx \\=\frac{e^x}{2}+\frac 12 \cdot \frac{\cos2x+2\sin2xe^x}{1^2+2^2}(1 \cdot \cos2x+2 \sin2x)~~[*]\\=\frac{e^x}{2}\left[1+\frac 15(\cos2x+2\sin2x)\right]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-aec3f61bfe94589d3924a3482ecc853e_l3.png)
Note[*]: ![]()
![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{3^x\cos3x}~dx\\=\int{e^{\log 3^x}\cos3x}~dx\\=\int{e^{x\log 3}\cos3x}~dx\\=\int{e^{(\log 3)x}\cos3x}~dx\\=\frac{e^{(\log 3)x}}{3^2+(\log 3)^2}[(\log 3)\cos3x+3\sin3x]\\=\frac{3^x}{9+(\log 3)^2}[(\log 3)\cos3x+3\sin3x]+c_1\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-bcca9e4c6a3a7b91e5db6f2be22471d4_l3.png)
![Rendered by QuickLaTeX.com I_2\\=\displaystyle\int{3^x \cos x}~dx\\=\int{e^{\log 3^x}\cos x}~dx\\=\int{e^{x\log 3}\cos x}~dx\=\int{e^{(\log 3)x}\cos x}~dx\\=\frac{e^{(\log 3)x}}{1^2+(\log 3)^2}[(\log 3)\cos x+\sin x]\=\frac{e^{(\log 3)x}}{1+(\log 3)^2}[(\log 3)\cos x+\sin x]+c_2\rightarrow(3)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-0a135f55deaab6cc3b662ac657c7834f_l3.png)
Hence, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{3^x \cos^3x}~dx\\=\frac 14 \cdot\frac{3^x}{9+(\log 3)^2}[(\log 3)\cos3x+3\sin3x]\\~~+\frac 34 \cdot\frac{e^{(\log 3)x}}{1+(\log 3)^2}[(\log 3)\cos x+\sin x]+c.~~[~c=c_1+c_2~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-34012f9d4ac82f19572e3a400436c880_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{e^x\sin x \sin2x}~dx\\=\frac 12 \int{e^x(2\sin x\sin2x)}~dx\\=\frac 12\int{e^x[\cos (2x-x)-\cos(2x+x) ]}~dx\\=\frac 12 \int{e^x(\cos x-\cos 3x)}~dx\\=\frac 12 \int{e^x \cos x}~dx-\frac 12 \int{e^x \cos 3x}~dx\\=\frac 12 \cdot \frac{e^x}{1^2+1^2}(1 \cdot \cos x+1 \cdot \sin x) -\frac 12 \cdot \frac{e^x}{1^2+3^2}(1 \cdot \cos3x+3 \cdot \sin3x)+c\\=\frac 14e^x(\cos x+\sin x)-\frac{1}{2} \cdot \frac{e^x}{10}(\cos3x+3\sin3x)+c.\\=\frac 14 e^x\left[\cos x+\sin x-\frac 15(\cos 3x+3\sin3x)\right]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-8e98f8aa4065ad44598fab1ef483ca29_l3.png)
![]()
Solution.
![]()
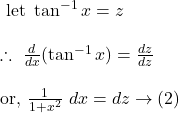
By ![]() we get,
we get,
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{\frac{e^{\tan^{-1}x}}{1+x^2} \cdot \frac{1}{1+x^2}}~dx\\=\displaystyle\int{\frac{e^z}{1+\tan^2z}}~dz\\=\int{\frac{e^z}{\sec^2z}}~dz\\=\int{e^z\cos^2z}~dz\\=\frac 12 \int{e^z(2\cos^2z)}~dz\\=\frac 12 \int{e^z(1+\cos2z)}~dz\\=\frac 12 \int{e^z}~dz+\frac 12 \int{e^z \cos2z}~dz\\=\frac{e^z}{2}+\frac 12 \cdot \frac{e^z}{1^2+2^2}(\cos2z+2\sin2z)+c\\=\frac{e^z}{2}+\frac 12 \cdot \frac{e^z}{5}(\cos2z+2\sin2z)+c\\=\frac{e^z}{2}\left[1+\frac{\cos2z+2\sin2z}{5}\right]+c\\=\frac 12 e^{z}\left[1+\frac 15 \left(\frac{1-\tan^2z}{1+\tan^2z}+2 \times\frac{2\tan z}{1+\tan^2z}\right)\right]+c\\=\frac 12 e^{\tan^{-1}x}\left[1+\frac 15\left(\frac{1-x^2}{1+x^2}+\frac{4x}{1+x^2}\right)\right]+c\\=\frac 12 e^{\tan^{-1}x} \left[1+\frac{1-x^2+4x}{5(1+x^2)}\right]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-d2b80c9038394e428b4cfa2d68d1bb11_l3.png)
![]()
Solution.
![]()
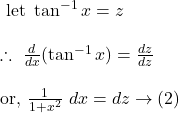
By ![]() we get,
we get,
![Rendered by QuickLaTeX.com ~I \\=\displaystyle\int{e^{2z}(1+\tan z)^2}~dx\\=\int{e^{2z}(1+2\tan z+\tan^2z)}~dz\\=\int{e^{2z}(1+\tan^2z+2\tan z)}~dz\\=\int{e^{2z}(\sec^2z+2\tan z)}~dz\\=\int{e^{2z}\sec^2z}~dz+2\int{e^{2z}\tan z}~dz\\=e^{2z}\int{\sec^2z}~dz-\int{\left[\frac{d}{dz}(e^{2z}) \int{\sec^2z}~dz\right]}~dz+2\int{e^{2z}\tan z}~dz\\=e^{2z}\tan z-2\int{e^{2z}\tan z}~dz+2\int{e^{2z}\tan z}~dz+c\\=e^{2z}\tan z+c\\=xe^{2\tan^{-1}x}+c](https://examhoop.com/wp-content/ql-cache/quicklatex.com-0ef6bb3a207760e829118e26bda94ab2_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{\csc^3x}~dx\\=\int{\csc x(\csc^2x)}~dx\\=\csc x \int{\csc^2x}~dx-\int{\left[\frac{d}{dx}(\csc x) \int{\csc^2x}~dx\right]}~dx\\=\csc x(-\cot x)-\int{(-\csc x \cot x)(-\cot x)}~dx\\=-\csc x \cot x-\int{\csc x(\cot^2x)}~dx\\=-\csc x \cot x-\int{\csc x(\csc^2x-1)}~dx\\=-\csc x \cot x-\int{\csc^3x}~dx+\int{\csc x}~dx\\=-\csc x \cot x-I+\log|\tan(x/2)|+c_1\\~~ \\ \therefore~ 2I=-\csc x \cot x+\log|\tan(x/2)|+c_1 \\ \text{or,}~~ I=\frac 12[\log|\tan(x/2)|-\csc x\cot x]+c.~~[~c=c_1/2~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-a7e3429f7cac393cec83e058cdf83ab2_l3.png)