In the previous article, we have discussed the solutions of Short Answer type questions of Integration By Parts Chapter of S N Dey mathematics Class 12. In this chapter, we will discuss the problems of Short Answer Type Questions.

Integration By Parts | Long Answer Type Questions’ Solution | S N Dey
![]()
Solution.
![]()

![]()
From ![]() we get,
we get,
![Rendered by QuickLaTeX.com ~I\\=\displaystyle\int{z^2\tan^{-1}z}~dz\\=(\tan^{-1}z) \int{z^2}~dz-\int{\left[\frac{d}{dx}(\tan^{-1}z) \int{z^2}~dx\right]}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\int{\frac{1}{1+z^2} \cdot \frac{z^3}{3}}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\frac 13 \int{\frac{z^3}{1+z^2}}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\frac 13\int{\frac{z(1+z^2)-z}{1+z^2}}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\frac 13 \int{z}~dz+\frac 13 \int{\frac{z}{1+z^2}}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\frac{z^2}{6}+\frac 16 \int{\frac{2z}{1+z^2}}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\frac{z^2}{6}+\frac 16 \int{\frac{d(1+z^2)}{1+z^2}}~dz\\=\frac{z^3}{3}(\tan^{-1}z)-\frac{z^2}{6}+\frac 16 \log|1+z^2|+c\\=\frac{\tan^3\theta}{3}(\theta)-\frac{\tan^2\theta}{6}+\frac 16 \log|1+\tan^2\theta|+c\\=\sin^{-1}x \cdot \frac{\sin^3\theta}{3\cos^3\theta}-\frac{\sin^2\theta}{6\cos^2\theta}+\frac 16 \log\left(1+\frac{\sin^2\theta}{\cos^2\theta}\right)+c\\=\sin^{-1}x \cdot \frac{x^3}{3(1-\sin^2\theta)^{3/2}}-\frac{x^2}{6(1-\sin^2\theta)}+\frac{1}{6} \log\left(\frac{\cos^2\theta+\sin^2\theta}{\cos^2\theta}\right)+c\\=\sin^{-1}x \cdot \frac{x^3}{3(1-x^2)^{3/2}}-\frac{x^2}{6(1-x^2)}+\frac 16 \log\left(\frac{1}{1-x^2}\right)+c\\=\frac 13\left[\left(\frac{x}{\sqrt{1-x^2}}\right)^3-\frac 12 \cdot \frac{x^2}{1-x^2}-\frac 12 \log (1-x^2)\right]+c](https://examhoop.com/wp-content/ql-cache/quicklatex.com-7133df891a19ffa43a395c0115a9c03c_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\csc^2x \log(\sec x)}~dx\\=\log(\sec x)\int{\csc^2 x}~dx-\int{\left[\frac{d}{dx}(\log(\sec x)) \int{\csc^2x}~dx\right]}~dx\\= \log(\sec x) \times (-\cot x)-\int{\frac{\sec x \tan x}{\sec x} \cdot (-\cot x)}~dx\\=-\cot x\log(\sec x)+\int{dx}\\=-\cot x\log(\sec x)+x+c\\=x-\cot x \log(\sec x)+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-17846c7699e5f880c454128a72f54ea0_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\frac{e^x}{x}(x\log x+1)}~dx\\=\int{e^x \log x}~dx+\int{\frac{e^x}{x}}~dx\\= \log x \int{e^x}~dx-\int{\left[\frac{d}{dx}( \log x) \int{e^x}~dx\right]}~dx +\int{(e^x/x)}~dx\\=\log x \cdot (e^x)-\int{\frac 1x \cdot e^x}~dx+\int{(e^x/x)}~dx\\=e^x \log x-\int{(e^x/x)}~dx+\int{(e^x/x)}~dx\\=e^x\log x+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-821d101647c10cb9806c5c37326ff31b_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\left[\frac{1}{\log x}-\frac{1}{(\log x)^2}\right]}~dx\\=\int{\frac{1}{\log x}}~dx-\int{\frac{1}{(\log x)^2}}~dx\\=\frac{1}{\log x} \int{dx}-\int{\left[\frac{d}{dx}\left(\frac{1}{\log x}\right) \int{dx}~\right]}~dx-\int{\frac{1}{(\log x)^2}}~dx \\=\frac{x}{\log x}+\int{\frac{1}{(\log x)^2} \cdot \frac 1x \cdot x}~dx-\int{\frac{1}{(\log x)^2}}~dx\\=\frac{x}{\log x}+\int{\frac{1}{(\log x)^2}}~dx-\int{\frac{1}{(\log x)^2}}~dx\\=\frac{x}{\log x}+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-3b8e024175ef3aae2eb9a6411a475dda_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\left[\log(\log x)+\frac{1}{(\log x)^2}\right]}~dx\\=\log(\log x) \int{dx}-\int{\left[\frac{d}{dx}(\log(\log x)) \int{}~dx\right]}~dx+\int{\frac{dx}{(\log x)^2}}\\=x\log(\log x)-\int{\frac{1}{\log x}} \cdot \frac 1x \cdot x~dx+\int{\frac{dx}{(\log x)^2}}\\=x\log(\log x)-\int{\frac{dx}{\log x}}+\int{\frac{dx}{(\log x)^2}}\\=x\log(\log x)-I_1+\int{\frac{dx}{(\log x)^2}}\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-dbea70f1ab4d43d987342147cb796501_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{\frac{dx}{\log x}}\\=\frac{1}{\log x} \int{dx}-\int{\left[\frac{d}{dx}\left(\frac{1}{\log x}\right) \int{}~dx\right]}~dx\\=\frac{x}{\log x}+ \int{\frac{1}{(\log x)^2} \cdot \frac 1x \cdot x}~dx\\=\frac{x}{\log x}+\int{\frac{dx}{(\log x)^2}} \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-22c4dfa007df48e900e3694fed2c4dc2_l3.png)
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{\left[\log(\log x)+\frac{1}{(\log x)^2}\right]}~dx\\=x\log(\log x)-\frac{x}{\log x}-\int{\frac{dx}{(\log x)^2}}+\int{\frac{dx}{(\log x)^2}}\\=x\log(\log x)-\frac{x}{\log x}+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c6ef36112b93da19d8fbb90358ccad86_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{e^x \left(\frac 1x-\frac{1}{x^2}\right)}~dx\\=\frac 1x \int{e^x dx}-\int{\left[\frac{d}{dx}(1/x) \int{e^x~}~dx\right]}~dx-\int{\frac{e^x}{x^2}}~dx\\=\frac{e^x}{x}+\int{\frac{e^x}{x^2}}~dx-\int{\frac{e^x}{x^2}}~dx\\=\frac{e^x}{x}+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-641d1e12d75385e5b8f6315e47ac9a01_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\frac{xe^x}{(x+1)^2}}~dx\\=\int{\frac{e^x(x+1)-e^x}{(x+1)^2}}~dx\\=\int{\frac{e^x}{(x+1)}}~dx-\int{\frac{e^x}{(x+1)^2}}~dx\\=\frac{1}{(x+1)} \int{e^x}~dx- \int{\left[\frac{d}{dx}\left(\frac{1}{x+1}\right) \int{e^x}~dx\right]}~dx-\int{\frac{e^x}{(x+1)^2}}~dx\\=\frac{e^x}{x+1}+\int{\frac{e^x}{(x+1)^2}}~dx-\int{\frac{e^x}{(x+1)^2}}~dx\\=\frac{e^x}{x+1}+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-22d3c3fcc722fdd3c11fdb0eb85b1592_l3.png)
![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{e^x \log \cos x}~dx\\=\log \cos x \int{e^x}~dx-\int{\left[\frac{d}{dx}(\log \cos x) \int{e^x}~dx\right]}~dx\\= e^x \log \cos x-\int{ \frac{1}{\cos x} \cdot (-\sin x) \cdot e^x}~dx\\=e^x \log \cos x+ \int{e^x \tan x}~dx \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-83d90d566645ffcc9597bbb433af2a31_l3.png)
Hence , by ![]() we get,
we get,
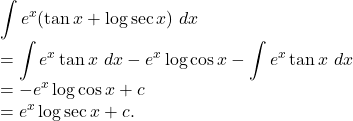
![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{e^x \csc^2(x/2)}~dx\\=e^x\int{\csc^2(x/2)}~dx- \int{\left[\frac{d}{dx}(e^x) \int{\csc^2(x/2)}~dx\right]}~dx\\=e^x \cdot \left(-\frac{\cot(x/2)}{1/2}\right)- \int{\left(-\frac{\cot(x/2)}{1/2}\right) \cdot e^x}~dx\\=-2 e^x \cot(x/2)+2 \int{e^x(\cot(x/2))}~dx \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-82d66e897e93c517caeedf84d5cc6d0c_l3.png)
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{e^x~\frac{1-\sin x}{1-\cos x}}~dx\\=\frac 12\left[-2 e^x \cot(x/2)+2 \int{e^x(\cot(x/2))}~dx \right]-\int{e^x \cot(x/2)}~dx\\=-e^x\cot(x/2)+\int{e^x \cot(x/2)}~dx-\int{e^x \cot(x/2)}~dx\\=-e^x\cot(x/2)+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-b79f9670cef7033aa4955bcdae391294_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{e^x\left(\frac{2-\sin2x}{1-\cos2x}\right)}~dx\\=\int{e^x \left(\frac{2-2\sin x\cos x}{2\sin^2x}\right)}~dx\\=\int{e^x\left(\frac{1-\sin x\cos x}{\sin^2x}\right)}~dx\\=\int{e^x \cdot \csc^2x}~dx-\int{e^x \cot x}~dx\\=e^x \int{\csc^2x}~dx-\int{\left[\frac{d}{dx}(e^x) \int{\csc^2x}~dx\right]}~dx-\int{e^x \cot x}~dx\\=-e^x\cot x+\int{e^x \cot x}~dx -\int{e^x \cot x}~dx\\=-e^x\cot x+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-03604e13e97374da4c7b5b17f7661fd7_l3.png)
![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\= \displaystyle\int{e^x~\sec^2(x/2)}~dx\\=e^x\int{\sec^2(x/2)}~dx-\int{\left[\frac{d}{dx}(e^x) \int{\sec^2(x/2)}~dx\right]}~dx\\=2e^x\tan(x/2)-2\int{e^x\tan(x/2)}~dx\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-2c912dc117ffba759100e71c34959979_l3.png)
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{e^x\left(\frac{1+\sin x}{1+\cos x}\right)}~dx\\=\frac 12\left[2e^x\tan(x/2)-2\int{e^x\tan(x/2)}~dx\right]+\int{e^x\tan(x/2)}~dx\\=e^x\tan(x/2)-\int{e^x\tan(x/2)}~dx+\int{e^x\tan(x/2)}~dx\\=e^x\tan(x/2)+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-1b96a120490d484a445d1020b56cef2a_l3.png)