Tangent and Normal | Part-1 Examhoop

In the previous article , we have solved few questions of Plane Chapter (Ex-2B) of S N De Mathematics(Chhaya). In the following article, we are going to discuss/solve Short Answer Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Tangent and Normal (Ex-14).

1. If $~px + qy = r~$ be a tangent to the circle $~x^2 + y^2 = a^2~$ at any given point then find the equation of the normal to the circle at the same point.

Solution.

Since the normal to the given circle is perpendicular to the straight line $~px+qy=r,~~$ so the equation of the normal can be written as $~qx-py+k=0 \longrightarrow(1)$

Since the normal (1) passes through the center of the circle i.e., $~(0,0)~$ , we get from (1),

$~ q \times 0-p \times 0+k=0 \Rightarrow k=0.$

$\therefore~~$ The equation of the normal to the circle is $~qx-py=0.$

2. If $~lx+my+n=0~$ be a tangent to the circle $~x^2+ y^2+2gx+2fy+c=0~$ at a given point on it, find the equation of the normal to the circle at the same point.

Solution.

By question, the equation of the normal can be written as $~mx-ly+k=0.$

Since the normal passes through the center of the circle i.e., $~(-g,-f)~$ ,

$\therefore~~ m(-g)-l(-f)+k=0 \\ \text{or,}~~ -mg+lf+k=0 \\ \text{or,}~~ k=mg-lf.$

Hence, the equation of the normal is given by

$~mx-ly+(mg-lf)=0 \Rightarrow mx-ly=lf-mg~~\text{(ans.)}$

MTG 45 + 21 Years JEE Main and IIT JEE Advanced Previous Years Solved Papers with Chapterwise Topicwise Solutions Mathematics Book- JEE Advanced PYQ Question Bank For 2023 Exam Paperback

3.(i) Find the points on the ellipse $~4x^2+9y^2=36~$ at which the tangents are parallel to x-axis. Also find the points on it where the tangents are parallel to y-axis.

Solution.

$~4x^2+9y^2=36 \longrightarrow(1)$

Let the tangents of (1) are parallel to x-axis at $~(x_1,y_1).$

$\therefore~~ \left[\frac{dy}{dx}\right]_{(x_1,y_1)}=0 \longrightarrow(2)$

Now, from (1) we get,

$~4 \cdot (2x)+ 9 \cdot \left(2y~\frac{dy}{dx}\right)=0 \\ \text{or,}~~ 4x+9y~\frac{dy}{dx}=0 \Rightarrow \frac{dy}{dx}=-\frac{4x}{9y} \longrightarrow(3)$

$\therefore~~ \left[\frac{dy}{dx}\right]_{(x_1,y_1)}= \left(-\frac{4x}{9y}\right)_{(x_1,y_1)}=-\frac{4x_1}{9y_1}.$

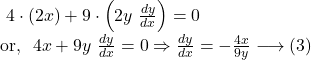
So, by (2) we get, $~~-\frac{4x_1}{9y_1}=0 \Rightarrow x_1=0.$

Since the point $~(x_1,y_1)~$ lies on $~(1)~$ ,

$~4x_1^2+9y_1^2=36 \longrightarrow(4)$

For $~x_1=0,~$ we get from (4),

$~4 \cdot 0+9y_1^2=36 \\ \text{or,}~~ y_1^2=\frac{36}{9}=4 \Rightarrow y_1=\pm \sqrt{4}=\pm 2.$

Hence, the required points are $~(0,2)~$ and $~(0,-2).$

2nd Part :

Let the tangents drawn at $~(x_1,y_1)~$ on the given ellipse are parallel to y-axis.

So, in this case, the slope

$~\left[\frac{dy}{dx}\right]_{(x_1,y_1)}=0\\ \text{or,}~~-\frac{9y_2}{4x_2}=0~~[\text{By (3)}] \\ \text{or,}~~ y_2=0.$

$~\because~(x_2,y_2)~$ lies on the given ellipse ,

$~4x_2^2+9y_2^2=0 \\ \text{or,}~~ 4x_2^2+9 \cdot 0=36 \\ ~~~\text{or,}~~ x_2^2 = \frac{36}{4}=9 \\ ~~~\therefore~~ x_2= \pm \sqrt{9}=\pm 3.$

Hence, the required points are $~(\pm 3,0).$

(ii) Is there any tangent parallel to x-axis to the parabola $y^2=20x?$ Give reasons for your answer.

Solution.

$~y^2=20x \longrightarrow(1)$

If possible, let the tangent to the parabola (1) is parallel to $~x-$ axis at the point $~(x_1,y_1).$

The slope of the tangent at $~(x_1,y_1)~$ is given by $~ \left[\frac{dy}{dx}\right]_{(x_1,y_1)}.$

In this case, $~\left[\frac{dy}{dx}\right]_{(x_1,y_1)}=0\longrightarrow(1)$

$~\text{Now,}~~ y^2=20x \Rightarrow 2y~\frac{dy}{dx}=20 \\~~~ \therefore~~ \frac{dy}{dx}=\frac{10}{y} \longrightarrow(2)$

From (1) and (2) we get, $~\frac{10}{y_1}=0~$ which is impossible.

Hence, there is no tangent parallel to $~x-$ axis to the parabola $~y^2=20x.$

Mtg 45 + 21 Years Jee Main And Iit Jee Advanced Previous Years Solved Papers With Chapterwise Topicwise Solutions Physics, Chemistry, Mathematics ( Set … Jee Advanced Pyq Question Bank For 2023 Exam )

(iii) Find where the normal to $~x^2+y^2-4x+6y+9=0~$ is parallel to x-axis.

Solution.

$~x^2+y^2-4x+6y+9=0 \longrightarrow(1)$

Differentiating both sides of (1) w.r.t. $~x~$ we get,

$~2x+2y~\frac{dy}{dx}-4+6~\frac{dy}{dx}=0 \\ \text{or,}~~ x+y~\frac{dy}{dx}-2+3~\frac{dy}{dx}=0 \\ \text{or,}~~ (y+3)~\frac{dy}{dx}=2-x \\ \therefore~~ \frac{dy}{dx}=\frac{2-x}{y+3} \longrightarrow(2)$

Suppose that the normal to the circle (1) is parallel to x-axis at $~(x_1,y_1).$

So, in this case, the slope of the normal

$~\left[-\frac{dx}{dy}\right]_{(x_1,y_1)}=0 \\ \text{or,}~~ -\frac{y_1+3}{2-x_1}=0 \Rightarrow y_1=-3.$

Since $~(x_1,y_1)~$ lies on (1),

$~x_1^2+y_1^2-4x_1+6y_1+9=0 \\ \text{or,}~~ x_1^2+(-3)^2-4x_1+6 \cdot (-3)+9=0 \\ \text{or,}~~ x_1^2+9-4x_1-18+9=0 \\ \text{or,}~~ x_1(x_1-4)=0 \Rightarrow ~ x_1=0,4.$

Hence, the required points are $~(0,-3)~$ and $~(4,-3).$

4.(i) Find where the tangent to the parabola $~y = x^2~$ is parallel to the line $~y=4x-5.$

Solution.

$~y=x^2 \longrightarrow(1),~~ y=4x-5 \longrightarrow(2)$

Let the tangent to the parabola (1) at the point $~(x_1,y_1)~$ is parallel to the line (2).

In this case, slope of the tangent at $~(x_1,y_1)~=~$ the gradient of the straight line (2).

$\therefore~ \left[\frac{dy}{dx}\right]_{(x_1,y_1)}=4 \\ \text{or,}~~ 2x_1=4~~(\text{By (1), (2)}) \\ \text{or,}~~ x_1=\frac 42=2.$

$\because~~ (x_1,y_1)~$ lies on the parabola (1), $~y_1=x_1^2=2^2=4.$

Hence, the coordinates of the required point is $~(2,4).$

(ii) Find the coordinates of points on the hyperbola $~xy=c^2~$ at which the normal is perpendicular to the line $~x+t^2y=2c.$

Solution.

$~xy=c^2 \longrightarrow(1)$

$x+t^2y=2c \\ \text{or,}~~ t^2y=-x+2c \\ \text{or,}~~ y=-\frac{1}{t^2} \cdot x+\frac{2c}{t^2} \longrightarrow(2)$

Suppose that normal to the hyperbola (1) at $~(x_1,y_1)~$ is perpendicular to the straight line (2).

$\therefore~$ Slope of normal to hyperbola (1) at $~(x_1,y_1)~ \times ~$ Slope of the straight line (2) $=-1$

$\therefore~~ \left[-\frac{dx}{dy}\right]_{(x_1,y_1)} \times \left(-\frac{1}{t^2}\right) =-1 \longrightarrow (3)$

$~\text{Now,}~~ xy=c^2 \\ \text{or,}~~ x \cdot \frac{dy}{dx}+y \cdot 1=0 \\ \text{or,}~~ \frac{dy}{dx}=-\frac yx \\ \text{or,}~~ \left[-\frac{dx}{dy}\right]_{(x_1,y_1)}=\frac{x_1}{y_1} \longrightarrow(4)$

Hence, from (3) and (4) we get,

$~\frac{x_1}{y_1} \times \frac{1}{t^2}=1 \Rightarrow x_1=y_1 t^2.$

Since the point $~(x_1,y_1)~$ lies on the hyperbola $~xy=c^2,$

$\therefore~~ x_1y_1=c^2 \\ \text{or,}~~ y_1t^2 \times y_1=c^2 \\ \text{or,}~~ y_1^2=\frac{c^2}{t^2} \Rightarrow y_1= \pm \frac ct.$

For $~y_1=\frac ct,~~ x_1= \frac ct \cdot t^2=ct.$

For $~y_1=-\frac ct,~~ x_1=-\frac ct \cdot t^2=-ct.$

Hence, the coordinates of the required points are $~\left(ct,\frac ct\right)~, ~\left(-ct,\frac ct\right).$

(iii) Prove that the tangent to the curve $~y^2=x^2-5x+6~$ at the points $~(2, 0)~$ and $~(3, 0)~$ are at right angles. [CBSE ’92]

Solution.

$~y=x^2-5x+6 \longrightarrow(1)$

Differentiating both sides of (1) w.r.t. $~x,~$ we get

$~\frac{dy}{dx}=2x-5$

$\therefore~~$ Slope of (1) at $~(2,0)~$ is given by

$~m_1=\left[\frac{dy}{dx}\right]_{(2,0)}=2 \times 2-5=4-5=-1.$

Again, slope of (1) at $~(3,0)~$ is given by

$~m_2=\left[\frac{dy}{dx}\right]_{(3,0)}=2 \times 3-5=6-5=1.$

$\because~~ m_1 \times m_2= (-1) \times 1=-1,~$ the result follows.

Tangent and Normal | Part-2

In this article , we have solved few VSA type Questions (5-15) of S N De Mathematics, Tangent and Normal Chapter (Ex-14 ).

S.N. De -Tangent and Normal (Part -1)-Class 12

In this book, full solutions of S.N. De -Tangent and Normal (Part -1) (Eng. Version)-Class 12 have been provided. This book contains solutions of (Ex-14) and have solutions of Very Short Answer Type Questions and Short Answer Type Questions. This book contains 82 pages along with a cover page .

Tangent and Normal | Part-1

In the previous article , we have solved few questions of Plane Chapter (Ex-2B) of S N De Mathematics(Chhaya). In the following article, we are going to discuss/solve Short Answer Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Tangent and Normal (Ex-14).

Tangent and Normal | Part-2

S.N. De -Tangent and Normal (Part -1)-Class 12

Tangent and Normal | Part-3

Tangent and Normal | Part-4

Tangent and Normal | Part-5

Tangent and Normal | Part-6

Tangent and Normal | Part-7

Tangent and Normal | Part-8

Tangent and Normal | Part-9

Leave a Comment Cancel reply