In the previous article, we discussed 9 short ans type questions of Short Answer Type Questions of Straight Line Chapter of Chhaya Mathematics, Class 11. In this article, we have solved few more.

Short Answer Type Questions of Straight Line Chapter- Ex 2A | S N De
10.The perimeter of the triangle formed by the straight line ![]() with the co-ordinate axes is
with the co-ordinate axes is ![]() unit ; find the value of
unit ; find the value of ![]()
Solution.

We have the equation of straight line
![]()
![]() the straight line intersects
the straight line intersects ![]() axis at
axis at ![]() and
and ![]() axis at
axis at ![]() making
making ![]() with origin at
with origin at ![]()
By the intercept form of Straight line ![]() , we see
, we see ![]()
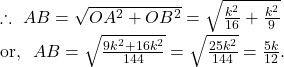
So, the perimeter of the triangle formed by the given straight line

Read More :
Straight Line | Part-4 |Ex-2A
Straight Line | Part-5 |Ex-2A
Straight Line | Part-6 |Ex-2A
Straight Line | Part-7 |Ex-2A
11.If ![]() for all positions of the moving line
for all positions of the moving line ![]() Show that the line always passes through a fixed point. Find the co-ordinates of that fixed point.
Show that the line always passes through a fixed point. Find the co-ordinates of that fixed point.
Solution.
We have
![]()
![Rendered by QuickLaTeX.com \text{Now,}~~ ax+by+c=0 \\ \text{or,}~~ ax+by-a-b=0 ~~[\text{By (1)}] \\ \text{or,}~~a(x-1)+b(y-1)=0 \\ \text{or,}~~(x-1)+\frac ba(y-1)=0 ~~ [~a \neq 0] \\ \text{or,}~~ (x-1)+\lambda (y-1)=0 \rightarrow(2) ~~ [\text{where}~~\lambda \neq 0]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-0a0c83dccb7e805f16e9d5df3a649072_l3.png)
Clearly, ![]() represents a straight line through the point of intersection of
represents a straight line through the point of intersection of ![]() Solving
Solving ![]() we get
we get ![]() and so, the required fixed point is
and so, the required fixed point is ![]()
12.Show that the straight line ![]() always passes through a fixed point; find the co-ordinates of that fixed point.
always passes through a fixed point; find the co-ordinates of that fixed point.
Solution.
![]()
Clearly, for different values of ![]() where
where ![]() and
and ![]() are not simultaneously zero,
are not simultaneously zero, ![]() represents straight lines through the point of intersection of the straight lines
represents straight lines through the point of intersection of the straight lines ![]() and
and ![]()
Now, solving ![]() and
and ![]() we get,
we get, ![]()
So, the co-ordinates of that fixed point is ![]()
13. Show that the equation of the straight line ![]() can be expressed in the following form :
can be expressed in the following form :
![]()
Solution.

![]()
14.If ![]() and
and ![]() be the length of the perpendiculars from the origin upon the lines
be the length of the perpendiculars from the origin upon the lines ![]() and
and ![]() respectively, show that
respectively, show that ![]()
Solution.
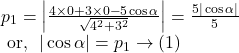

Hence, by ![]() and
and ![]() we get,
we get,

15. Find the equation of the straight line through the point ![]() and the point of intersection of the lines
and the point of intersection of the lines ![]() and
and ![]() Also find the length of the portion of the line intercepted between the co-ordinate axes.
Also find the length of the portion of the line intercepted between the co-ordinate axes.
Solution.
The equation of the straight line through the point of intersection of the straight lines ![]() and
and ![]() is
is
![]()
Since the straight line ![]() passes through the point
passes through the point ![]() , so
, so

Hence, putting the value of ![]() in
in ![]() we get
we get

So, ![]() represents the intercept form of straight line that cuts
represents the intercept form of straight line that cuts ![]() axis at
axis at ![]() and
and ![]() axis at
axis at ![]()
So, ![]()
16.If the straight line ![]() passes through the point of intersection of the lines
passes through the point of intersection of the lines ![]() and
and ![]() find
find ![]()
Solution.
The equation of the straight line through the point of intersection of the straight lines ![]() and
and ![]() is
is
![]()
Now the straight line ![]() and
and ![]() are identical.
are identical.
So, ![]()
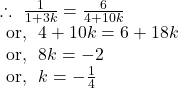
Again,
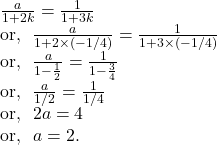
17.Find the equation of the straight line which passes through the point of intersection of the straight lines ![]() and
and ![]() and makes equal intercepts upon the co-ordinate axes.
and makes equal intercepts upon the co-ordinate axes.
Solution.


18.Find the equation of the straight line which makes intercepts on the axes equal in magnitude but opposite in sign and passes through the point of intersection of the lines ![]() and
and ![]() Also find the perpendicular distance of the line from the origin.
Also find the perpendicular distance of the line from the origin.
Solution.

