Straight Line | Part-3 |Ex-2A Examhoop

In the previous article, we discussed 9 short ans type questions of Short Answer Type Questions of Straight Line Chapter of Chhaya Mathematics, Class 11. In this article, we have solved few more.

19.A ray of light start from $~P(1,2)~$ , reflect on $~x-$ axis at $~A~$ and hence passing through $~Q(5,3)~$ find the co-ordinates of $~A.$

Solution.

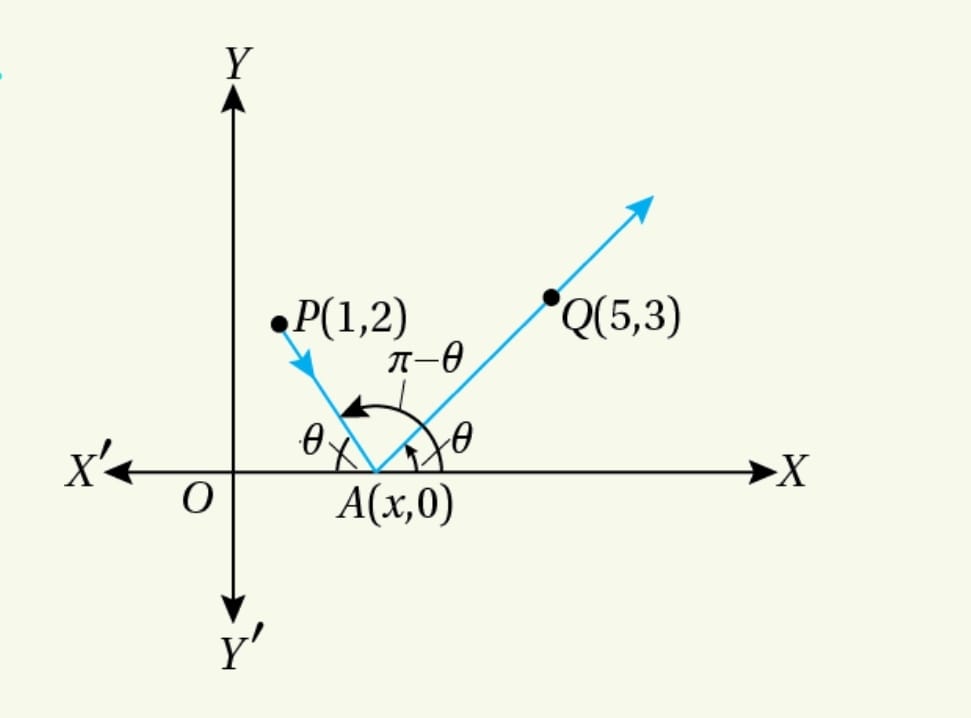
According to the problem, $~A~$ lies on $~x-$ axis. Let the co-ordinates of $~A~$ be $~(x,0).$

$~\therefore~\tan\theta=\frac{3-0}{5-x}=\frac{3}{5-x} \rightarrow(1)$ and

$\tan(\pi-\theta)=\frac{2-0}{1-x} \\ \text{or,}~~-\tan\theta=\frac{2}{1-x} \\ \text{or,}~~-\frac{3}{5-x}=\frac{2}{1-x}~~[\text{By (1)}] \\ \text{or,}~~ -3+3x=10-2x \\ \text{or,}~~5x=13 \\ \text{or,}~~x=\frac{13}{5}$

Hence, $~A\equiv \left(\frac{13}{5},0\right).$

20. Find the equation to the straight lines which are at a distance of $~2~$ unit from the origin and which pass through the point of intersection of the lines $~3x+4y=4~$ and $~2x+5y+2=0.$

Solution.

We have the equations of straight lines $~3x+4y=4\rightarrow(1)~$ and $~2x+5y+2=0\rightarrow(2).$

Solving $~(1)~$ and $~(2)~$ we get, $~x=4,~y=-2.$

Now, the straight lines passing through the point of intersection of the given lines must pass through the point $~(4,-2).$

Any straight line through the point $~(4,-2)~$ can be written as $~y+2=m(x-4)\rightarrow(3)~$ where $~m~$ is the slope of the straight line.

Equation $~(3)~$ can be written as $~mx-y-4m-2=0\rightarrow(4)$

Perpendicular distance from origin to the straight line $~(4),~$ is $~\frac{|4m+2|}{\sqrt{m^2+1}}.$

According to the problem,

$\frac{|4m+2|}{\sqrt{m^2+1}}=2 \\ \text{or,}~~ (4m+2)^2=4(m^2+1) \\ \text{or,}~~ (4m)^2+2 \cdot 4m \cdot 2+2^2=4m^2+4 \\ \text{or,}~~ 16m^2+16m+4=4m^2+4 \\ \text{or,}~~12m^2+16m=0 \\ \text{or,}~~ 4m(3m+4)=0 \\ \text{or,}~~ m(3m+4)=0 \\ \text{or,}~~ m=0, -\frac 43.$

For $~m=0,~$ the equation of straight line $~y+2=0~[\text{By (3)}]$

For $~m=-4/3,~$ the equation of straight line

$~y+2=-\frac 43(x-4)~[\text{By (3)}] \\ \text{or,}~~ 4x+3y=10.$

21. Find the equation of the straight line through the point of intersection of the lines $~2y-3x+16=0~$ and $~3x+y=1~$ and through the centroid of the triangle whose vertices are $~(4,3),~(2,-7)~$ and $~(-9,-20).$

Solution.

The equation of the straight line through the point of intersection of the lines $~2y-3x+16=0~$ and $~3x+y=1~$ is

$~2y-3x+16 +k(3x+y-1)=0 \\ \text{or,}~~ (3k-3)x+(k+2)y+16-k=0 \rightarrow(1)$

Now, centroid of the triangle whose vertices are $~(4,3),~(2,-7)~$ and $~(-9,-20)~$ is $~\left(\frac{4+2-9}{3},\frac{3-7-20}{3}\right)=(-1,-8).$

Since the straight line $~(1)~$ passes through the point $~(-1,-8)~$ , so

$(3k-3)\times(-1)+(k+2) \times (-8)+16-k=0 \\ \text{or,}~~ -3k+3-8k-16+16-k=0 \\ \text{or,}~~ -12k=-3 \\ \text{or,}~~ k=\frac{1}{4}.$

So, putting the value of $~k~$ , we get the required equation of the straight line which is

$\left(\frac 34-3\right)x+\left(\frac 14+2\right)y+16-\frac 14=0 \\ \text{or,}~~ -9x+9y+63=0 \\ \text{or,}~~ x-y-7=0 \\ \text{or,}~~ x-y=7.$

22. Examine whether the straight lines $~x-y+4=0,~ 2x+3y-6=0~$ and $~8x+7y-26=0~$ are concurrent or not.

Solution.

Solving $~x-y+4=0,~ 2x+3y-6=0~$ we get, $~x=-\frac 65,~y=\frac{14}{5}.$ Putting these values of $~x, ~y~$ in the straight line $~8x+7y-26=0~$ we get,

$~-8 \times \frac{6}{5}+7 \times \frac{14}{5}-26\\~~=-\frac{48}{5}+\frac{98}{5}-26\\~~=\frac{-48+98-130}{5}\\~~=-16$

So, $~x=-\frac 65,~y=\frac{14}{5}~$ does not satisfy the equation of the third straight line and hence we can conclude that the straight lines $~x-y+4=0,~ 2x+3y-6=0~$ and $~8x+7y-26=0~$ are not concurrent.

23. For what value of $~a~$ the three straight lines $~7x-11y+3=0,~4x+3y-9=0~$ and $~13x+ay-48=0~$ pass through the same point ?

Solution.

Solving $~7x-11y+3=0,~4x+3y-9=0~$ we get, $~x=\frac{18}{13},~y=\frac{15}{13}.$

Since the three straight lines pass through the same point, so
the third straight line passes through the point $~\left(\frac{18}{13},~\frac{15}{13}\right).$

$\therefore~\frac{13 \times 18}{13}+\frac{a \times 15}{13}-48=0 \\ \text{or,}~~ 234+15a-624=0 \\ \text{or,}~~ 15a=390 \\ \text{or,}~~ a=\frac{390}{15}=26.$

24. If the straight lines $~a_1x+b_1y+c=0,~a_2x+b_2y+c=0~$ and $~a_3x+b_3y+c=0~~[c \neq 0]~$ are concurrent, show that the points $~(a_1,b_1),~(a_2,b_2)~$ and $~(a_3,b_3)~$ are collinear.

Solution.

Since the straight lines $~a_1x+b_1y+c=0,~a_2x+b_2y+c=0~$ and $~a_3x+b_3y+c=0~~[c \neq 0]~$ are concurrent, suppose that the common point is $~(h, k).$

$\therefore~ a_1h+b_1k+c=0 \rightarrow(1),~a_2h+b_2k+c=0 \rightarrow(2),a_3h+b_3k+c=0 \rightarrow(3).$

From $~(1),~(2),~(3)~$ we can say that the general solution of $~xh+ yk +c=0~$ is $~x=a_1,y=b_1 ;~ x=a_2,y=b_2 ~$ and $~x=a_3,y=b_3.$

Again, $~xh+yk+c=0~$ represents a straight line on which the points $~(a_1,b_1),~(a_2,b_2),~(a_3,b_3)~$ lie.

Hence, the points $~(a_1,b_1),~(a_2,b_2)~$ and $~(a_3,b_3)~$ are collinear.

25. Show that the equation of the straight line through $~(\alpha,\beta)~$ and through the point of intersection of the lines $~a_1x+b_1y+c_1=0~$ and $~a_2x+b_2y+c_2=0~$ is

$~\frac{a_1x+b_1y+c_1}{a_1\alpha+b_1\beta+c_1}=\frac{a_2x+b_2y+c_2}{a_2 \alpha+b_2\beta+c_2}.$

Solution.

Equation of any straight line passing through the point of intersection of intersection of the lines $~a_1x+b_1y+c_1=0~$ and $~a_2x+b_2y+c_2=0~$ is

$~ a_1x+b_1y+c_1+k(a_2x+b_2y+c_2)=0 \rightarrow(1)$

Now, if the straight line $~(1)~$ passes through the point $~(\alpha,\beta)~$ then

$~ a_1\alpha+b_1\beta+c_1+k(a_2\alpha+b_2\beta+c_2)=0 \\ \text{or,}~~ k=-\frac{a_1\alpha+b_1\beta+c_1}{a_2\alpha+b_2\beta+c_2}$

Now, putting the value of $~k~$ in $~(1),$ we get

$a_1x+b_1y+c_1-\frac{a_1\alpha+b_1\beta+c_1}{a_2\alpha+b_2\beta+c_2} (a_2x+b_2y+c_2)=0 \\ \therefore~ \frac{a_1x+b_1y+c_1}{a_1\alpha+b_1\beta+c_1}=\frac{a_2x+b_2y+c_2}{a_2 \alpha+b_2\beta+c_2}.$

Post Views: 179

Leave a Comment Cancel reply