In the following article, we are going to discuss/solve few Short Answer Type Questions of S.N.Dey Mathematics-Class 12 . In the previous article , we have completed solution of VSA type Questions.

1. Find the coordinates of the foot of the perpendicular and the perpendicular distance of the point ![]() from the plane
from the plane ![]() Find also the image of the point in the plane.
Find also the image of the point in the plane.
Solution.
Let ![]() be the image of the point
be the image of the point ![]() in the plane
in the plane ![]()
PO is perpendicular to the plane and S is the midpoint of PO and the foot of the perpendicular.
Direction ratios of PS are ![]()
![]() the equation of PS are
the equation of PS are
![]()
The general point on line is ![]()
If this point lies on plane, then
![]()
So, the coordinates of S are ![]()
As S is the midpoint of PO ![]()
By comparing both sides , we get
![]()
So, the image of the point ![]()
![]() Perpendicular distance between two points is
Perpendicular distance between two points is
![]()
Read More : Complete S N Dey Solution of Plane (Ex-5A) Chapter with PDF link
2. Show that, ![]() is the circum-centre of the triangle formed by the points
is the circum-centre of the triangle formed by the points ![]() and
and ![]()
Solution.
Let ![]()
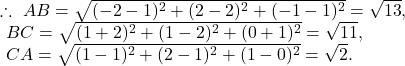
![]()
![]() is a right angled triangle with hypotenuse
is a right angled triangle with hypotenuse ![]()
So, circum centre of the triangle is the midpoint of AB.
![]() the circum-centre of the triangle is
the circum-centre of the triangle is
![]()
MTG 45 + 21 Years JEE Main and IIT JEE Advanced Previous Years Solved Papers with Chapterwise Topicwise Solutions Physics Book – JEE Advanced PYQ Question Bank For 2023 Exam Paperback
3. Find the equations of the three planes which are parallel to the coordinate axes and which pass through the points ![]() and
and ![]()
Solution.
For Planes parallel to x-axis :
The direction ratios of x-axis are ![]() So, the equation of the plane parallel to the x-axis and passing through the points
So, the equation of the plane parallel to the x-axis and passing through the points ![]() and
and ![]() is
is

For Planes parallel to y-axis :
The direction ratios of y-axis are ![]() So, the equation of the plane parallel to the y-axis and passing through the points
So, the equation of the plane parallel to the y-axis and passing through the points ![]() and
and ![]() is
is
![Rendered by QuickLaTeX.com \begin{vmatrix} x-3 & y-1 & z-1 \\ 3-1& 1+2 & 1-3 \\ 0& 1 &0 \\ \end{vmatrix}=0 \\ \text{or,}~~\begin{vmatrix} x-3 &y-1 &z-1 \\ 2 &3 &-2 \\ 0& 1 &0 \\ \end{vmatrix}=0 \\ \text{or,}~~- \begin{vmatrix} x-3& z-1 \\ 2& -2 \\ \end{vmatrix} =0 \\ \text{or,}~~-[-2(x-3)-2(z-1)]=0 \\ \text{or,}~~ 2(x-3)+2(z-1)=0 \\ \text{or,}~~ x-3+z-1=0 \Rightarrow x+z=4.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-1c9e84066a3c42ca57d5379e2484acb4_l3.png)
For Planes parallel to z-axis :
The direction ratios of z-axis are ![]() So, the equation of the plane parallel to the z-axis and passing through the points
So, the equation of the plane parallel to the z-axis and passing through the points ![]() and
and ![]() is
is

4. Let ![]() be the coordinates of the foot of the perpendicular drawn from the origin to a plane. Find equation of that plane.
be the coordinates of the foot of the perpendicular drawn from the origin to a plane. Find equation of that plane.
Solution.
Since ![]() is the coordinates of the foot of the perpendicular drawn from the origin to the plane, the direction ratios of the normal to the plane are
is the coordinates of the foot of the perpendicular drawn from the origin to the plane, the direction ratios of the normal to the plane are ![]() or,
or, ![]()
Let ![]() be the equation of the plane which passes through the point
be the equation of the plane which passes through the point ![]()
![]()
So, the equation of the plane is given by ![]()
5. Show that the equation of the plane passing through the point (1, 2, 3) and parallel to the plane 3x+4y-5z=3 is given by 3x+4y-5z=-4.
Solution.
The equation of the plane parallel to ![]() can be written as
can be written as ![]()
Since the plane (1) passes through the point ![]() ,
,
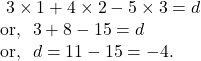
So, the equation of the plane is given by ![]()
Physics Galaxy 2023 : JEE Advanced – Physics – Chapter wise PYQ Analysis by Ashish Arora Paperback
6. Find the equation of the plane passing through the points ![]() and
and ![]() and perpendicular to the plane
and perpendicular to the plane ![]() convert the equation to vector form.
convert the equation to vector form.
Solution.
The equation of any plane passing through the point ![]() is
is
![]() where
where ![]() are constants.
are constants.
Since the plane (1) passes through the point ![]()
![]()
Since the plane (1) is perpendicular to the plane ![]() so
so
![]()
From ![]() and
and ![]() , we get by cross-multiplication,
, we get by cross-multiplication,

Hence, by (1) we get the cartesian equation of plane as follows :

Hence, the vector equation of the plane is
![]()
7. Prove that the equation of the plane which passes through the points ![]() and
and ![]() and which is perpendicular to the plane
and which is perpendicular to the plane ![]() is
is ![]()
Solution.
Equation of any plane passing through the point ![]() is
is ![]() where
where ![]() are constants.
are constants.
If the plane (1) passes through the point ![]()
![]()
Again, the plane (1) is perpendicular to the given plane ![]()
![]()
From (2) and (3), we get by cross-multiplication,

Hence, the equation of the plane is

8. Prove that the equation of the plane which passes through the point ![]() and is perpendicular to the planes
and is perpendicular to the planes ![]() and
and ![]() is
is ![]()
Solution.
The equation of any plane passing through the point ![]() is
is
![]() where
where ![]() are constants.
are constants.
Since the plane (1) is perpendicular to the planes ![]() and
and ![]() so
so
![]()
Now, from (2) and (3) we get by cross-multiplication,

So, the equation of the plane is

9. Show that the planes ![]() and
and ![]() are perpendicular to
are perpendicular to ![]() and
and ![]() planes respectively.
planes respectively.
Solution.
For the plane ![]() , the direction ratios of the normal to the plane are
, the direction ratios of the normal to the plane are ![]()
For xy-plane, the direction ratios of the normal to the plane are ![]()
Now, ![]()
So, the plane ![]() is perpendicular to the xy-plane.
is perpendicular to the xy-plane.
For the plane ![]() , the direction ratios of the normal to the plane are
, the direction ratios of the normal to the plane are ![]()
For yz-plane, the direction ratios of the normal to the plane are ![]()
Now, ![]()
So, the plane ![]() is perpendicular to the yz-plane.
is perpendicular to the yz-plane.
For the plane ![]() , the direction ratios of the normal to the plane are
, the direction ratios of the normal to the plane are ![]()
For zx-plane, the direction ratios of the normal to the plane are ![]()
Now, ![]()
So, the plane ![]() is perpendicular to the zx-plane.
is perpendicular to the zx-plane.

