In the previous article , we have completed the discussions about the Short Answer Type Questions. In this article, we will discuss 10 Long Answer type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Long Answer Type Questions (1-10) | Circle | S N Dey Solution
1.Find the equation to the circles which touch the ![]() axis and pass through
axis and pass through ![]() and
and ![]()
Solution.

The equation of the circle touching the ![]() axis can be written as
axis can be written as
![]() where
where ![]() is the centre of the circle with radius
is the centre of the circle with radius ![]() unit.
unit.
Since the circle passes through ![]() ,
,
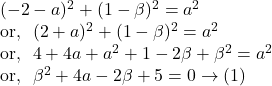
Again, since the circle passes through ![]() ,
,

Subtracting ![]() from
from ![]() we get
we get

Now, from ![]() and
and ![]() we get,
we get,

![]() , corresponding values of
, corresponding values of ![]()
So, the required equation of circle (for ![]() ) is
) is

and also the required equation of circle (for ![]() ) is
) is

2. If two straight lines ![]() and
and ![]() lie along two diameters of a circle , which touches the
lie along two diameters of a circle , which touches the ![]() axis, find the equation of the circle.
axis, find the equation of the circle.
Solution.
According to the problem, center of the circle will be the point where both lines cross each other. Now, solving two straight lines ![]() and
and ![]() we get,
we get, ![]()

So, the centre of the circle ![]()
Since, the circle touches ![]() axis, so the equation of the circle is
axis, so the equation of the circle is
![]()
3. A circle touches the lines ![]() and
and ![]() If the centre of the circle lies in the first quadrant , show that there are two such circles and find their equations . Specify which of these is inscribed within the triangle formed by the given lines.
If the centre of the circle lies in the first quadrant , show that there are two such circles and find their equations . Specify which of these is inscribed within the triangle formed by the given lines.
Solution.
Since the circle touches both ![]() axis and
axis and ![]() axis , the centre of the circle is
axis , the centre of the circle is ![]() So, the equation of the circle is
So, the equation of the circle is ![]()
Since ![]() is a tangent to the circle
is a tangent to the circle ![]() so the distance of
so the distance of ![]() from the centre
from the centre ![]() of the circle = the radius of the circle.
of the circle = the radius of the circle.

So, the equation of the circle ![]() where
where ![]()
Now, since the points ![]() and
and ![]() lie on the same side of the straight line
lie on the same side of the straight line ![]() , the circle with radius
, the circle with radius ![]() unit is inscribed within the triangle formed by the given lines.
unit is inscribed within the triangle formed by the given lines.
4. Find the equations to the circles which which touch the axis of ![]() at a distance
at a distance ![]() from the origin and intercept a length
from the origin and intercept a length ![]() unit on the axis of
unit on the axis of ![]()
Solution.

Let the equation of the circle be ![]()
![]()
![]()
Now, the the length of the intercept on ![]() axis
axis

By ![]() we get two circles by two corresponding values of
we get two circles by two corresponding values of ![]()
![]() Using
Using ![]() two circles are given by
two circles are given by
![]()
5. A circle passes through the point ![]() and touches the straight line
and touches the straight line ![]() at the point
at the point ![]() . Find its equation.
. Find its equation.
Solution.

6. Find the equation of the circle which touches the ![]() axis at a distance
axis at a distance ![]() unit from the origin and cuts off an intercept of length
unit from the origin and cuts off an intercept of length ![]() unit from the
unit from the ![]() axis.
axis.
Solution.

Let the equation of the circle be ![]()
The circle ![]() can be written as
can be written as
![]()
The length of the intercept on ![]() axis
axis
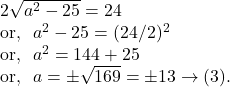
So, by ![]() and
and ![]() we get the equation of the circle as follows :
we get the equation of the circle as follows :
![]()
7. Show that the circles ![]() and
and ![]() touch each other externally ; find the co-ordinates of their point of contact.
touch each other externally ; find the co-ordinates of their point of contact.
Solution.
Two given circles are
![]()
Comparing ![]() with
with ![]() we get,
we get,

So, for the circle ![]() centre
centre ![]() and radius
and radius ![]()
Comparing ![]() with
with ![]() we get,
we get,

So, for the circle ![]() centre
centre ![]() and radius
and radius ![]()
Distance (![]() ) between the centres of two circles
) between the centres of two circles

So, two circles touch each other externally.
Again, ![]() so that the co-ordinates of their point of contact is
so that the co-ordinates of their point of contact is
![]()
8. Prove that the circles ![]() and
and ![]() touch each other internally. Find the equation of their common tangent.
touch each other internally. Find the equation of their common tangent.
Solution.
Two given circles are
![]()
Comparing ![]() with
with ![]() we get,
we get,

So, for the circle ![]() centre
centre ![]() and radius
and radius ![]()
In a similar way, from ![]() we get, the centre
we get, the centre ![]() and radius
and radius ![]()
Distance (![]() ) between the centres of two circles
) between the centres of two circles
![]()
Hence, by ![]() we can conclude that two circles touch each other internally.
we can conclude that two circles touch each other internally.
Now, subtracting ![]() from
from ![]() we get
we get
![]()
So, the equation in ![]() , represents the equation of their common tangent.
, represents the equation of their common tangent.
9. If the circles ![]() and
and ![]() touch each other , prove that ,
touch each other , prove that , ![]()
Solution.
Two given circles are
![]()
The centre of the circle ![]() is
is ![]() and the radius
and the radius ![]()
The centre of the circle ![]() is
is ![]() and the radius
and the radius ![]()

10. Prove that the circles ![]() and
and ![]() touch each other. Find the co-ordinates of the point of contact.
touch each other. Find the co-ordinates of the point of contact.
Solution.
Two given equation of circles are ![]() and
and ![]()
Clearly, centre of circle ![]() is
is ![]()
and radius ![]() is
is
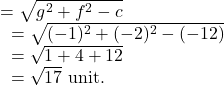
Again, the circle ![]() can be rewritten as
can be rewritten as ![]() ans so centre of circle
ans so centre of circle ![]() is
is ![]()
Also, the radius (![]() ) of circle of
) of circle of ![]() is
is
![]()
![]()
Distance between the centres ![]() of two circles are
of two circles are
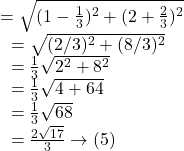
So, from ![]() and
and ![]() we get,
we get, ![]()
So, two circles touch each other internally.
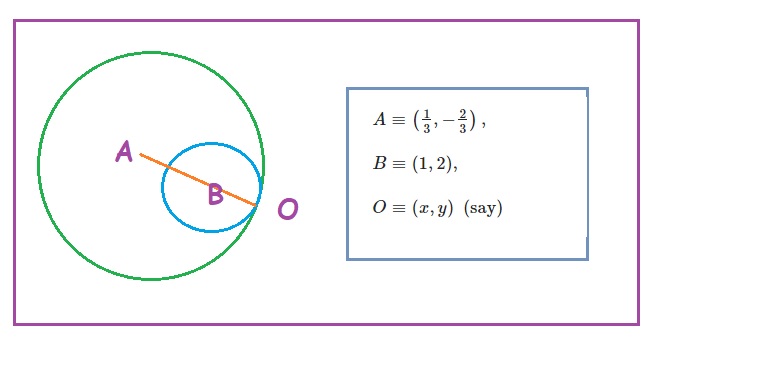
From the figure, we notice that
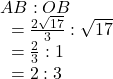
Suppose that two circles touch each other at the point ![]()
![]()
From ![]() we get
we get
![]()
Hence, the co-ordinates of the point of contact is ![]()
To download full PDF solution of Circle (Chhaya Mathematics, Class 11 ), click here.