In the previous article , we discussed about 10 Long Answer Type Questions. In this article, we will discuss few more Long Answer type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Circle Related Long Answer Type Questions (11-20) | S N Dey Mathematics
11. Show that the circle ![]() touches the co-ordinate axes. Also find the equation of the circle which passes through the common points of intersection of the above circle and the straight line
touches the co-ordinate axes. Also find the equation of the circle which passes through the common points of intersection of the above circle and the straight line ![]() and which also passes through the origin.
and which also passes through the origin.
Solution.
The equation of the given circle can be written as ![]()
From ![]() we get the centre of the circle
we get the centre of the circle ![]() is
is ![]() and radius
and radius ![]() unit.
unit.
Now, if ![]() , we get from the given equation of the circle,
, we get from the given equation of the circle,
![]()
As we have just one point common between ![]() axis and circle, it means it touches
axis and circle, it means it touches![]() axis at
axis at ![]()
Similarly, if ![]() , we get from the given equation of the circle,
, we get from the given equation of the circle,
![]()
As we have just one point common between ![]() axis and circle, it means it touches
axis and circle, it means it touches![]() axis at
axis at ![]()
Hence, the given circle touches the two axes.
Now, the equation of the circle passing through the intersection of the given circle and the straight line ![]() is
is
![]()
Since the circle ![]() passes through the point
passes through the point ![]() , we get from
, we get from ![]()
![]()
Hence, the equation of the circle is

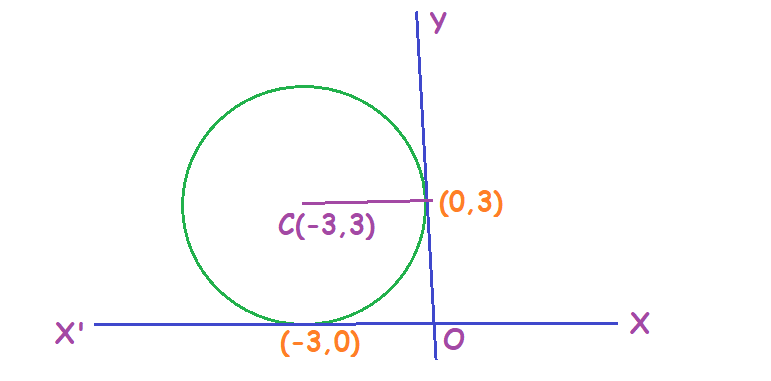
12. A circle through the common points of the circles ![]() and
and ![]() has its centre on the line
has its centre on the line ![]() Find the centre and radius of the circle.
Find the centre and radius of the circle.
Solution.
Any circle through the common points of the circles ![]() and
and ![]() can be written as
can be written as
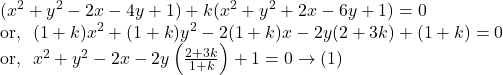
Comparing ![]() with
with ![]() , we get
, we get
![]()
So, centre of the circle ![]() is
is ![]()
Since the centre of the circle ![]() lies on the line
lies on the line ![]() ,
,
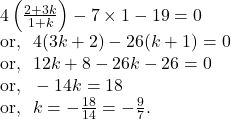
Hence, the centre of the circle ![]()

Also, the radius of the circle is
![]()
13. The circle ![]() and the line
and the line ![]() intersect at
intersect at ![]() and
and ![]() . Find the equation of the circle on
. Find the equation of the circle on ![]() as diameter.
as diameter.
Solution.
The equation of the given straight line ![]()
The equation of the given circle is ![]()
From ![]() we get,
we get, ![]()
From ![]() and
and ![]() we get,
we get,

Now, by ![]() we get for
we get for ![]()
Similarly, for ![]()
![]()
So, the equation of the circle on ![]() as diameter is given by
as diameter is given by
![Rendered by QuickLaTeX.com (x-\sqrt{7})(x+\sqrt{7})+[y-(\sqrt{7}+1)][y-(-\sqrt{7}+1)]=0 \\ \text{or,}~~ x^2-(\sqrt{7})^2+[(y-1)-\sqrt{7}][(y-1)+\sqrt{7}]=0 \\ \text{or,}~~ x^2-7+(y-1)^2-(\sqrt{7})^2=0 \\ \text{or,}~~ x^2-7+y^2-2y+1-7=0 \\ \therefore x^2+y^2-2y-13=0.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-928407863d6196a4724743359ca7bdfd_l3.png)
14. Find the equation to the circle described on the common chord of the circles ![]() and
and ![]() as a diameter.
as a diameter.
Solution.
Two given equations of circles are
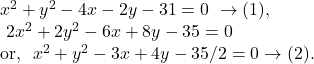
So, by ![]() we get the equation of common chord which is
we get the equation of common chord which is ![]()
Equation of any circle through the intersection of two given circles are

From ![]() we get the centre of circle
we get the centre of circle ![]() which lies on the common chord
which lies on the common chord ![]()

Now, putting the value of ![]() in
in ![]() we get
we get

15. Find the equation to the locus of the mid-points of chords drawn through the point ![]() on the circle
on the circle ![]()
Solution.
Let ![]() be the chord passing through the point
be the chord passing through the point ![]()
Any point ![]() on the circle
on the circle ![]() can be written as
can be written as ![]()
If ![]() is the co-ordinates of mid-point of
is the co-ordinates of mid-point of ![]() , then
, then
![]()
Then from ![]() we get,
we get,
![Rendered by QuickLaTeX.com \sin^2\theta+\cos^2\theta=1 \\ \text{or,}~~[\frac 12(k-2)]^2+(h/2)^2=1 \\ \text{or,}~~ h^2+(k-2)^2=4 \\ \text{or,}~~ h^2+k^2-4k+4=4 \\ \text{or,}~~ h^2+k^2=4k \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-79f449c17da0748cfdc5adbc2bcbcbb5_l3.png)
Hence, by ![]() we can say that the equation to the locus of the mid-points of chords is
we can say that the equation to the locus of the mid-points of chords is ![]()
16. A circle passes through the origin ![]() and intersects the co-ordinate axes at
and intersects the co-ordinate axes at ![]() and
and ![]() . If the length of the diameter of the circle be
. If the length of the diameter of the circle be ![]() unit, then find the locus of the centroid of the triangle
unit, then find the locus of the centroid of the triangle ![]()
Solution.
Any circle passing through the origin can be written as ![]()
Let ![]()
Since the circle ![]() passes through the points
passes through the points ![]() so
so
![]()

If ![]() be the centroid of
be the centroid of ![]() , then
, then
![]()
So, by ![]() we get,
we get,

![]() the locus of the centroid of the triangle
the locus of the centroid of the triangle ![]() is
is ![]()
17. Find the equation of a circle circumscribing the triangle whose sides are ![]() and
and ![]() If
If ![]() vary so that
vary so that ![]() , find the locus of the centre of the circle.
, find the locus of the centre of the circle.
Solution.


18.Find the area of the equilateral triangle inscribed in the circle ![]()
Solution.

The equation of the given circle is ![]()
The centre of the circle ![]() is
is ![]() and radius
and radius ![]()
Now, from the figure , we note that in ![]()

So, the area of the equilateral triangle inscribed in the circle is
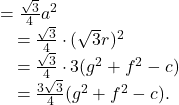
19. Find the area of the equilateral triangle inscribed in the circle ![]()
Solution.
Comparing the given circle with the standard form of the circle ![]() we get,
we get,
![]()
So, the radius ![]()
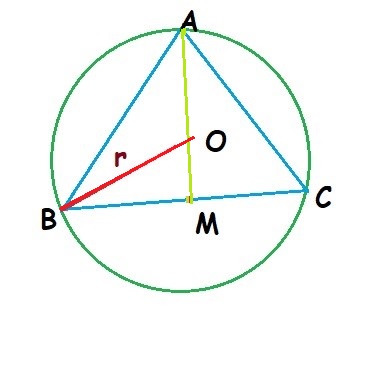
Now, from the figure (![]() ) we notice that
) we notice that
![]()
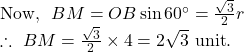
So, the length ![]() of the side of
of the side of ![]() is
is ![]()
So, the area of the equilateral triangle inscribed in the circle

20. Prove analytically that the straight line joining the middle point of a chord of a circle of a circle with the centre is perpendicular to the chord.
Solution.
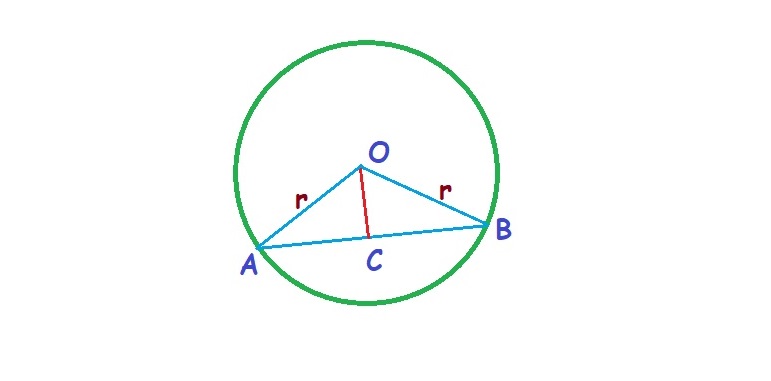
To prove : ![]() Given that
Given that ![]()
From ![]() and
and ![]() , we get
, we get
![]()
![]()

Hence, ![]()