In this article, we will do few solutions of Short Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11.

![]() Find
Find ![]() the lengths of axes
the lengths of axes ![]() the length of latus rectum
the length of latus rectum ![]() coordinates of vertices
coordinates of vertices ![]() eccentricity
eccentricity ![]() co-ordinates of foci and
co-ordinates of foci and ![]() equations of directrices of each of the following ellipses :
equations of directrices of each of the following ellipses :
![]()
Solution (a).
The given equation of the ellipse can be written as ![]()
Comparing ![]() with the general form of the ellipse
with the general form of the ellipse ![]() we get,
we get,
![]()
Clearly, major axis of the ellipse ![]() is along
is along ![]() axis , minor axis of the given ellipse is along
axis , minor axis of the given ellipse is along ![]() axis and the centre of the ellipse is at
axis and the centre of the ellipse is at ![]()
(i) The length of the major axis is ![]() and
and
the length of the minor axis is ![]()
(ii) The length of the latus rectum is
![]()
(iii) The co-ordinates of vertices ![]()
(iv) Eccentricity of the ellipse is given by
![]()
(v) The co-ordinates of foci are given by
![]()
(vi) Equations of directrices are given by

Solution(b)
The given equation of the ellipse can be written as ![]()
Comparing ![]() with the general form of the ellipse
with the general form of the ellipse ![]() we get,
we get,
![]()
Clearly, major axis of the ellipse ![]() is along
is along ![]() axis , minor axis of the given ellipse is along
axis , minor axis of the given ellipse is along ![]() axis and the centre of the ellipse is at
axis and the centre of the ellipse is at ![]()
For S N De Free PDF (Bengali Version )download for Ellipse Chapter , click here.
(i) The length of the major axis is ![]() and
and
the length of the minor axis is ![]()
(ii) The length of the latus rectum is
![]()
(iii) The co-ordinates of vertices ![]()
(iv) Eccentricity of the ellipse is given by
![]()
(v) The co-ordinates of foci are given by
![]()
(vi) Equations of directrices are given by

Solution(c)
The given equation of the ellipse can be written as ![]()
Comparing ![]() with the general form of the ellipse
with the general form of the ellipse ![]() we get,
we get,
![]()
Clearly, major axis of the ellipse ![]() is along
is along ![]() axis , minor axis of the given ellipse is along
axis , minor axis of the given ellipse is along ![]() axis and the centre of the ellipse is at
axis and the centre of the ellipse is at ![]()
(i) The length of the major axis is ![]() and
and
the length of the minor axis is ![]()
(ii) The length of the latus rectum is
![]()
(iii) The co-ordinates of vertices ![]()
(iv) Eccentricity of the ellipse is given by
![]()
(v) The co-ordinates of foci are given by
![]()
(vi) Equations of directrices are given by

Solution(d)
The given equation of the ellipse can be written as ![]()
Comparing ![]() with the general form of the ellipse
with the general form of the ellipse ![]() we get,
we get,
![]()
Clearly, major axis of the ellipse ![]() is along
is along ![]() axis , minor axis of the given ellipse is along
axis , minor axis of the given ellipse is along ![]() axis and the centre of the ellipse is at
axis and the centre of the ellipse is at ![]()
(i) The length of the major axis is ![]() and
and
the length of the minor axis is ![]()
(ii) The length of the latus rectum is
![]()
(iii) The co-ordinates of vertices ![]()
(iv) Eccentricity of the ellipse is given by
![]()
(v) The co-ordinates of foci are given by
![]()
(vi) Equations of directrices are given by

![]() Find the eccentricity and equations of the directrices of the ellipse
Find the eccentricity and equations of the directrices of the ellipse ![]() Show that the sum of the focal distances of any point on this ellipse is a constant.
Show that the sum of the focal distances of any point on this ellipse is a constant.
Solution.
Comparing the given equation of ellipse with the general form of the ellipse ![]() we get,
we get,
![]()
Eccentricity of the ellipse is given by
![]()
Equation of the directrix is given by
![]()
Any point on the given ellipse can be written as ![]()
The co-ordinates of the foci are given by
![]()
Now, the sum of the focal distances of the point P is
![Rendered by QuickLaTeX.com =\sqrt{(10\cos\theta-8)^2+36\sin^2\theta}+\sqrt{(10\cos\theta+8)^2+36\sin^2\theta}\\=\sqrt{64\cos^2\theta-160\cos\theta+100}+\sqrt{64\cos^2\theta+160\cos\theta+100}~~[*]\\=\sqrt{(8\cos\theta-10)^2}+\sqrt{(8\cos\theta+10)^2}\\=10-8\cos\theta+8\cos\theta+10~~[\because~ \cos\theta \leq 8< 10]\\=20=\text{constant}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-7fa6e4e767055779788948edcfcf6715_l3.png)
Note[*] :
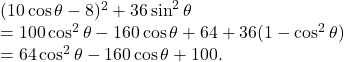
![]() Taking major and minor axes as
Taking major and minor axes as ![]() and
and ![]() -axes respectively, find the equation of the ellipse
-axes respectively, find the equation of the ellipse
![]() whose length of major and minor axes are
whose length of major and minor axes are ![]() and
and ![]() respectively.
respectively.
Solution.
By question, the equation of the ellipse can be written as
![]()
(i) The length of the major axis ![]()
and the length of the minor axis ![]()
Hence, by ![]() the equation of the ellipse is
the equation of the ellipse is

![]() whose lengths of minor axis and latus rectum are
whose lengths of minor axis and latus rectum are ![]() and
and ![]()
Solution.
Length of the minor axis ![]()
Length of the latus rectum ![]()
Hence, the equation of the ellipse is given by

![]() whose eccentricity is
whose eccentricity is ![]() and co-ordinates of foci are
and co-ordinates of foci are ![]()
Solution.
By question, the equation of the ellipse can be written as
![]()
The eccentricity ![]()
The co-ordinates of foci ![]()
![]()

So, the equation of the ellipse is given by
![]()
![]() whose eccentricity is
whose eccentricity is ![]() and length of latus rectum
and length of latus rectum ![]()
Solution.
![Rendered by QuickLaTeX.com e=\frac{1}{\sqrt{2}} \\ \text{or,}~~ e^2=\frac 12 \\ \text{or,}~~ 1-\frac{b^2}{a^2}=\frac 12 \\ \text{or,}~~ \frac {b^2}{a^2}=1-\frac 12=\frac 12 \rightarrow(1) \\ \text{or,}~~ \frac 1a \cdot \frac{2b^2}{a}=1 \\ \text{or,}~~ \frac 1a \cdot 3=1~[*]\\ \text{or,}~~ a=3.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-26e326adf48d50a6dc8ce05109a03f37_l3.png)
Note[*] : ![]()
Again, ![]()
Hence, the equation of the ellipse is
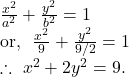
![]() which passes through the points
which passes through the points ![]() and
and ![]()
Solution.
The equation of the ellipse can be written as ![]()
Since the ellipse ![]() passes through the points
passes through the points ![]() and
and ![]()
![]()
From ![]() and
and ![]() we get
we get

Similarly, from ![]() and
and ![]() we get
we get

Hence, replacing the values of ![]() and
and ![]() , we get from
, we get from ![]()
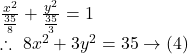
Finally, from ![]() we get the required equation of ellipse whose major axis is along
we get the required equation of ellipse whose major axis is along ![]() axis and minor axis is along
axis and minor axis is along ![]() -axis.
-axis.
![]() whose eccentricity is
whose eccentricity is ![]() and passes through the point
and passes through the point ![]()
Solution.
By question,

Since the ellipse ![]() passes through the point
passes through the point ![]() so
so
![Rendered by QuickLaTeX.com ~\frac{(-3)^2}{a^2}+\frac{1^2}{b^2}=1 \\~~~~~~ \text{or,}~~ \frac{9}{a^2}+\frac{1}{b^2}=1 \\~~~~~~ \text{or,}~~ 9 \times \frac{3}{5b^2}+\frac{1}{b^2}=1 ~~[~\text{By (1)}] \\ ~~~~~~\text{or,}~~ \frac{27+5}{5b^2}=1 \\~~~~~~ \text{or,}~~ \frac{32}{5b^2}=1 \\~~~~~~ \therefore~ \frac{1}{b^2}=\frac{5}{32}\rightarrow(3)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c1c4e9ba89e63a9a3eb5755a2eb1ec2d_l3.png)
Hence, using ![]() and
and ![]() we get the required equation of ellipse which is
we get the required equation of ellipse which is
![]()
![]() whose co-ordinates of vertices are
whose co-ordinates of vertices are ![]() and the co-ordinates of the ends of minor axes are
and the co-ordinates of the ends of minor axes are ![]()
Solution.
By question, the co-ordinates of the vertices ![]() the co-ordinates of the end of minor axes
the co-ordinates of the end of minor axes ![]()
![]()
Hence, the equation of the ellipse is
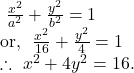
![]() whose distance between the foci is
whose distance between the foci is ![]() and the distance between the directrices is
and the distance between the directrices is ![]()
Solution.
By question, the distance between the foci is ![]() and the distance between the directrices is
and the distance between the directrices is ![]()
From ![]() and
and ![]() we get,
we get,
![]()
Again, from ![]() we get,
we get,

So, the equation of the ellipse is given by

![]() whose eccentricity is
whose eccentricity is ![]() and the sum of squares of major and minor axes is
and the sum of squares of major and minor axes is ![]()
Solution.
By question,


From ![]() and
and ![]() we get,
we get,

Hence, the equation of the ellipse is given by
![]()
![]() whose co-ordinates of vertices are
whose co-ordinates of vertices are ![]() and the co-ordinates of one focus are
and the co-ordinates of one focus are ![]()
Solution.
By question, the equation of the ellipse can be taken in the form ![]()
The co-ordinates of the vertices ![]() i.e.
i.e. ![]()
The co-ordinates of one focus ![]()
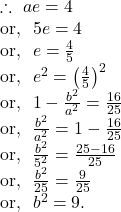
Hence, by ![]() we get the required equation of ellipse
we get the required equation of ellipse
![]()
![]() whose length of latus rectum is
whose length of latus rectum is ![]() unit and the co-ordinates of one focus are
unit and the co-ordinates of one focus are ![]()
Solution.
The length of latus rectum
![]()
Co-ordinates of one focus ![]()
![Rendered by QuickLaTeX.com \therefore~ ae=4 \\ \text{or,}~~ a^2e^2=4^2 \\ \text{or,}~~ a^2\left(1-\frac{b^2}{a^2}\right)=16\\ \text{or,}~~ a^2-b^2=16 \\ \text{or,}~~a^2-\frac 95a=16 \\ \text{or,}~~ 5a^2-9a-80=0 \\ \text{or,}~~ 5a^2-25a+16a-80=0 \\ \text{or,}~~ 5a(a-5)+16(a-5)=0 \\ \text{or,}~~ (5a+16)(a-5)=0 \\ \therefore a=5~~ [\because~ 5a+16 \neq 0]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-f6fbc9d3cfae49416cd1a43d47cab13e_l3.png)
So, ![]()
Hence, the equation of the ellipse is
![]()
(xii) whose distance between the foci is ![]() unit and minor axis is of length 4 unit.
unit and minor axis is of length 4 unit.
Solution.
The length of the minor axis ![]()
Distance between the foci ![]()

Hence, the equation of the ellipse is
![]()
![]() whose eccentricity is
whose eccentricity is ![]() and the length of semi-latus rectum is
and the length of semi-latus rectum is ![]() unit.
unit.
Solution.
Eccentricity ![]()

The length of semi-latus rectum

From ![]() and
and ![]() we get,
we get,
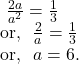
So, ![]()
Hence, the equation of the ellipse is
![]()