Ellipse (S.N.Dey) | Part-3

In the previous article , we solved few solutions of Short Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.

4(i) Find the lengths of axes of the ellipse whose eccentricity is $~\frac 35~$ and the distance between focus and directrix is $~16.$

Solution.

The distance between focus and directrix $=\frac ae-ae$

By question,

$\frac ae-ae=16 \\ \text{or,}~~ a\left(\frac 1e-e\right)=16 \\ \text{or,}~~ a\left(\frac 53-\frac 35\right)=16 \\ \text{or,}~~ a\times \frac{25-9}{15}=16 \\ \text{or,}~~ a \times \frac{16}{15}=16 \\ \text{or,}~~a=15.$

$~ e=\frac 35 \Rightarrow e^2=\left(\frac 35\right)^2 \\ \text{or,}~~ 1-\frac{b^2}{a^2}=\frac{9}{25} \\ \text{or,}~~ \frac{b^2}{a^2}=1-\frac{9}{25} \\ \text{or,}~~ \frac{b^2}{a^2}=\frac{16}{25} \\ \text{or,}~~ b=\frac 45 \times a \\ \therefore~ b=\frac 45 \times 15=12.$

Hence, the length of the major axis $(2a)=2 \times 15=30~\text{unit}~$ and the length of the minor axis $(2b)=2 \times 12=24~\text{unit}.$

$(ii)~~(1,3)~$ and $~(4,-1)~$ are two foci of an ellipse whose eccentricity is $~\frac 14.~$ Find the length of the major axis.

Solution.

Eccentricity $(e)=\frac 14.$

The distance between the two given foci is

$2ae=\sqrt{(4-1)^2+(-1-3)^2} \\ \text{or,}~~ 2 \cdot a \cdot \frac 14=\sqrt{9+16}=5 \\ \therefore~ 2a=20.$

Hence, the length of the major axis $~(2a)=20~~\text{unit}.$

5. The length of the latus rectum of an ellipse is $~8~$ unit and that of the major axis, which lies along the $~x-$ axis , is $~18~$ unit. Find its equation in the standard form . Determine the co-ordinates of the foci and the equations of its directrices.

Solution.

The length of the latus rectum of the ellipse is given by

$\frac{2b^2}{a}=8 \\ \text{or,}~~ b^2=4a=4 \times 9 ~~[\because ~2a=18] \\ \therefore~ b^2=36.$

Again, the length of the major axis (2a) is given by

$2a=18 \\ \Rightarrow a=\frac{18}{2}=9.$

Hence,the equation of the ellipse is

$\frac{x^2}{81}+\frac{y^2}{36}=1 \\ \text{or,}~~ 4x^2+9y^2=324.$

The eccentricity $(e)$ of the ellipse is given by

$e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{36}{81}}=\sqrt{\frac{45}{81}} \\ \therefore ~e=\sqrt{\frac 59}=\frac{\sqrt{5}}{3}.$

The co-ordinates of the foci of the ellipse is given by

$(\pm ae,0)=\left(\pm 9 \times \frac{\sqrt{5}}{3},0\right)=(\pm 3\sqrt{5},0).$

The equation of the directrix is given by

$x=\pm \frac ae=\pm \frac{3}{\sqrt{5}} \times 9 \\ \therefore~ \sqrt{5}x=\pm 27.$

6. Taking major and minor axes along $~y~$ and $~x~$ axes, find the equation of the ellipse whose

$(i)~$ co-ordinates of foci are $~(0, \pm 1)~$ and the length of minor axis is $~2.$

Solution.

Since the foci of the given ellipse lie on the $~y$ -axis , the major axis of the ellipse lies on the $~y-$ axis.

Again, the centre of the ellipse is given by $~\left(\frac{0+0}{2},\frac{1-1}{2}\right)~$ i.e. $~(0,0).$

So, the ellipse is of the form $~\frac{x^2}{b^2}+\frac{y^2}{a^2}=1~(a^2>b^2)\rightarrow(1)$

So, the co-ordinates of the foci $~(0,\pm ae)=(0,\pm 1).$

The length of the minor axis is given by

$2b=2 \Rightarrow b=1.$

$\text{Now,}~ae=1 \Rightarrow a^2e^2=1 \\ \text{or,}~~ a^2\left(1-\frac{b^2}{a^2}\right)=1 \\ \text{or,}~~ a^2-b^2=1 \\ \text{or,}~~ a^2-1^2=1 \\ \text{or,}~~ a^2=1+1=2.$

Hence, using $~(1)~$ , the equation of the ellipse is

$\frac{x^2}{1}+\frac{y^2}{2}=1 \\ \text{or,}~~ 2x^2+y^2=2.$

$(ii)~$ eccentricity $~\sqrt{\frac 37}~$ and the length of latus rectum $~\frac{8}{\sqrt{7}}.$

Solution.

$e=\sqrt{\frac 37} \\ \text{or,}~~ e^2=\frac 37 \\ \text{or,}~~ 1-\frac{b^2}{a^2}=\frac 37 \\ \text{or,}~~ \frac{b^2}{a^2}=1-\frac 37 =\frac 47\rightarrow(1)$

Length of latus rectum

$\frac{2b^2}{a}=\frac{8}{\sqrt{7}} \\ \text{or,}~~ b^2=\frac{4}{\sqrt{7}} \cdot a \rightarrow(2)$

From $~(1)~$ and $~(2)~$ we get,

$~\frac 47=\frac{1}{a^2} \times \frac{4a}{\sqrt{7}} \\ \text{or,}~~ a=\sqrt{7} \\ \text{or,}~~ a^2=7.$

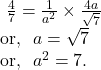
So, the equation of the ellipse is

$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1 \\ \text{or,}~~ \frac{x^2}{4}+\frac{y^2}{7}=1 \\ \text{or,}~~ 7x^2+4y^2=28.$

$(iii)~$ length of minor axis is $~2~$ and the distance between the foci is $~\sqrt{5}.$

Solution.

By the condition, length of minor axis $(2b)$ is given by

$2b=2 \Rightarrow b=1.$

The distance between the foci is

$2ae=\sqrt{5} \\ \text{or,}~~ (2ae)^2=(\sqrt{5})^2 \\ \text{or,}~~ 4a^2e^2=5 \\ \text{or,}~~ 4a^2\left(1-\frac{b^2}{a^2}\right)=5 \\ \text{or,}~~ 4a^2-4b^2=5 \\ \text{or,}~~ 4a^2-4 \times 1^2=5 \\ \text{or,}~~ 4a^2=5+4 \\ \text{or,}~~ a^2=\frac 94.$

Hence, the equation of the ellipse is given by

$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1 \\ \text{or,}~~ \frac{x^2}{1^2}+\frac{y^2}{\frac 94}=1 \\ \text{or,}~~ x^2+\frac 49 \cdot y^2=1 \\ \text{or,}~~ 9x^2+4y^2=9.$

$(iv)~$ co-ordinates of one vertex are $~(0,-6)~$ and the co-ordinates of one end of minor axis are $~(-3,0).$

Solution.

By question, the equation of the ellipse can be taken as $~\frac{x^2}{b^2}+\frac{y^2}{a^2}=1\rightarrow(1)$

Co-ordinates of one vertex is $~(0,-6)~$ and co-ordinates of one end of minor axis is $~(-3,0).$

$\therefore~ a=6,~b=3.$

Hence, by $~(1)~$ we get,

$~\frac{x^2}{3^2}+\frac{y^2}{6^2}=1 \\ \text{or,}~~ \frac{x^2}{9}+\frac{y^2}{36}=1 \\ \text{or,}~~ 4x^2+y^2=36.$

$(v)~$ co-ordinates of foci are $~(0, \pm 8)~$ and the eccentricity is $~\frac 45.$

Solution.

By question, the co-ordinates of foci $(0,\pm ae)=(0,\pm 8).$

$\therefore~ ae=8\rightarrow(1) \\ \text{or,}~~ a \cdot \frac 45=8 \\ \text{or,}~~ a=10$

$~a^2e^2=8^2~~[\text{By (1)}] \\ \text{or,}~~ a^2\left(1-\frac{b^2}{a^2}\right)=64\\ \text{or,}~~ a^2-b^2=64 \\ \text{or,}~~ 10^2-b^2=64 \\ \text{or,}~~ b^2=100-64=36$

Hence, the equation of the ellipse is

$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1 \\ \text{or,}~~ \frac{x^2}{36}+\frac{y^2}{100}=1 \\ \text{or,}~~ \frac{25x^2+9y^2}{900}=1 \\ \text{or,}~~ 25x^2+9y^2=900.$

$7.~$ Find the equation of the ellipse whose

$(i)~$ eccentricity is $~\frac 12,~$ focus is $~(2,0)~$ and directrix is $~x-8=0.$

Solution.

Let $~P(x,y)~$ be any point on the ellipse . The co-ordinates of the focus : $~S(2,0)~$ and the equation of the directrix is given by $~x-8=0\rightarrow(1)$

Now, the length of the perpendicular from P on the straight line (1) is given by

$PM=\frac{|x-8|}{\sqrt{1}}=|x-8|~$ ,

$SP=\sqrt{(x-2)^2+(y-0)^2}=\sqrt{(x-2)^2+y^2}$

Now, for the ellipse, we have

$\frac{SP}{PM}=e=\frac 12 \text{(given)} \\ \text{or,}~~ SP^2=\left(\frac 12\right)^2PM^2 \\ \text{or,}~~ (x-2)^2+y^2=\frac 14(x-8)^2 \\ \text{or,}~~ 4(x^2-4x+4+y^2)=x^2-16x+64 \\ \text{or,}~~ 4x^2-16x+16+4y^2=x^2-16x+64 \\ \text{or,}~~ 3x^2+4y^2=48.$

Hence, the equation of the ellipse is given by $~3x^2+4y^2=48.$

$(ii)~$ eccentricity is $~\frac{\sqrt{7}}{4},~$ focus is $~(0,-\sqrt{7})~$ and directrix is $~\sqrt{7}y+16=0.$

Solution.

Let $~P(x,y)~$ be any point on the ellipse. The co-ordinates of the focus : $~S(0,-\sqrt{7}).$

The equation of the directrix is $~ \sqrt{7}y+16=0\rightarrow(1)$

The length of the perpendicular from P on the straight line (1) is

$PM=\frac{|\sqrt{7}y+16|}{\sqrt{7}}~$ ,

$SP=\sqrt{(x-0)^2+(y+\sqrt{7})^2}=\sqrt{x^2+(y+\sqrt{7})^2}$

Now, for the ellipse

$\frac{SP}{PM}=e=\frac{\sqrt{7}}{4}~\text{(given)} \\ \text{or,}~~ \frac{SP^2}{PM^2}=\frac{7}{16} \\ \text{or,}~~ 16 SP^2=7PM^2 \\ \text{or,}~~ 16[x^2+(y+\sqrt{7})^2]=7 \times \frac{(\sqrt{7}y+16)^2}{7} \\ \text{or,}~~ 16x^2+16(y^2+2\sqrt{7}y+7)=7y^2+2\sqrt{7}y \times 16 +16^2 \\ \text{or,}~~ 16x^2+16y^2+32\sqrt{7}y+112=7y^2+32\sqrt{7}y+256 \\ \text{or,}~~ 16x^2+9y^2=144.$

Hence, the equation of the ellipse is $~16x^2+9y^2=144.$

$(iii)~$ eccentricity is $~\frac 12,~$ focus is $~(-1,1)~,$ directrix is $~x-y+3=0.$

Solution.

Let $~P(x,y)~$ be any point on the ellipse. The co-ordinates of focus : $~S(-1,1).$ The equation of the directrix : $~x-y+3=0\rightarrow(1)$

The perpendicular distance of the point P from the straight line (1) is

$PM=\frac{|x-y+3|}{\sqrt{1^2+(-1)^2}}=\frac{|x-y+3|}{\sqrt{2}},$

$SP=\sqrt{(x+1)^2+(y-1)^2}$

Now, for the ellipse, we know that

$\frac{SP}{PM}=e=\frac 12~~\text{(Given)} \\ \text{or,}~~ SP^2=\left(\frac 12\right)^2 PM^2 \\ \text{or,}~~ 4[(x+1)^2+(y-1)^2]=\frac 12(x-y+3)^2 \\ \text{or,}~~ 8(x^2+2x+1)+8(y^2-2y+1)=(x-y)^2+2(x-y) \cdot 3+3^2 \\ \text{or,}~~ 8x^2+16x+8+8y^2-16y+8=x^2+y^2-2xy+6x-6y+9 \\ \text{or,}~~ 7x^2+7y^2+2xy+10x-10y+7=0.$

$(iv)~$ focus is $~(3,4)~,$ directrix is $~3x+4y=5~$ and eccentricity is $~\frac 23.$

Solution.

Let $~P(x,y)~$ be any point on the ellipse. The co-ordinates of focus : $~S(3,4).$ The equation of the directrix : $~3x+4y=5\rightarrow(1)$

The perpendicular distance of the point P from the straight line (1) is

$PM=\frac{|3x+4y-5|}{\sqrt{9+16}}=\frac{|3x+4y-5|}{5},~~SP=\sqrt{(x-3)^2+(y-4)^2}$

Now, for the ellipse, we know that

$\frac{SP}{PM}=e=\frac 23~~[\text{given}] \\ \text{or,}~~ SP^2=\frac 49 PM^2 \\ \text{or,}~~9[(x-3)^2+(y-4)^2]=\frac{4(3x+4y-5)^2}{25} \\ \text{or,}~~ 225(x^2-6x+9+y^2-8y+16)=4(9x^2+16y^2+25+24xy-40y-30x) \\ \text{or,}~~ 189x^2-96xy+161y^2-1230x-1640y+5525=0\rightarrow(2)$

Hence, the equation $(2)$ represents the required ellipse.

Post Views: 119

Ellipse (S.N.Dey) | Part-3 | Ex-5

In the previous article , we solved few solutions of Short Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.

Leave a Comment Cancel reply