Ellipse (S.N.Dey) | Part-4 | Ex-5

by
In the previous article , we solved few solutions of Short Answer Type Questions of Ellipse Chapter of  S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.
Ellipse-S N dey

8.~ A point moves so that its distance from ~(0,-3)~ is ~\frac{1}{\sqrt{2}}~ times its distance from the line ~3x-4y+1=0.~ Show that the locus of the moving point is an ellipse whose equation you are to determine.

Solution.

Let the co-ordinates of any point be ~(h,k)~ so that distance of the point from the point ~(0,-3)~ is 

s=\sqrt{(h-0)^2+(k+3)^2}=\sqrt{h^2+(k+3)^2}~~\text{unit}

Again, distance of the point ~(h,k)~ from the line is

d=\frac{|3h-4k+1|}{\sqrt{3^2+(-4)^2}}=\frac{|3h-4k+1|}{\sqrt{9+16}}=\frac{|3h-4k+1|}{5} \rightarrow(1)

By question,

s=\frac{d}{\sqrt{2}} \\ \text{or,}~~ \sqrt{2}s=d \\ \text{or,}~~ 2s^2=d^2 \\ \text{or,}~~ 2[h^2+(k+3)^2]=\frac{(3h-4k+1)^2}{25} \\ \text{or,}~~ 50(h^2+k^2+6k+9)=(3h-4k+1)^2 \\ \text{or,}~~ 50h^2+50k^2+300k+450=9h^2+16k^2+1+1 \times 3h \times (-4k)+2 \times (-4k) \times 1+2 \times 3h \times 1 \\ \text{or,}~~ 41h^2+34k^2+24hk-6h+308k+449=0.

Hence, the equation of the moving point is an ellipse and is given by 

41x^2+34y^2+24xy-6x+308y+449=0.

9.~ Find the equation of the ellipse whose major axis is parallel to ~x-axis and 

(i)~ centre is ~(-3,2)~, eccentricity is ~\frac{\sqrt{7}}{4}~ and the length of latus rectum is ~\frac 92.

(ii)~ centre is ~(-2,1)~, length of major axis ~2\sqrt{3}~ and the co-ordinates of foci are ~(-1,1)~ and ~(-3,1).

Solution (i)

The length of the latus rectum \left(\frac{2b^2}{a}\right)=\frac 92 \rightarrow(1)

 e=\frac{\sqrt{7}}{4} \Rightarrow e^2=\frac{7}{16} \\ \text{or,}~~1-\frac{b^2}{a^2}=\frac{7}{16} \\ \text{or,}~~ 1-\frac{7}{16}=\frac 1a \cdot \frac{9}{4}~~[\text{By (1)}] \\ \text{or,}~~ \frac{9}{16}=\frac{9}{4a} \\ \text{or,}~~ 4a=16 \\ \text{or,}~~ a=\frac{16}{4}=4.

\therefore b^2=\frac 94 a=\frac 94 \times 4=9.

Hence, the equation of the ellipse is given by 

\frac{(x+3)^2}{16}+\frac{(y-2)^2}{9}=1

Solution(ii)

\text{Centre :}(\alpha,\beta)=(-2,1) \Rightarrow \alpha=-2,~ \beta=1.

The length of the major axis (2a)=2\sqrt{3} \Rightarrow a=\sqrt{3}\rightarrow(1)

The distance between the foci is 

2ae=\sqrt{(-1+3)^2+(1-1)^2}=2 \\ \text{or,}~~ ae=1 \\ \text{or,}~~ a^2e^2=1^2 \\ \text{or,}~~ a^2\left(1-\frac{b^2}{a^2}\right)=1 \\ \text{or,}~~ a^2-b^2=1 \\ \text{or,}~~ 3-b^2=1~~[\text{By (1)}] \\ \text{or,}~~ b^2=3-1 \\ \text{or,}~~ b^2=2.

Hence, the equation of the ellipse is ~\frac{(x+2)^2}{3}+\frac{(y-1)^2}{2}=1.

10.~ Find the equation of the ellipse , for which the foci are ~(0,1)~ and ~(0,-1)~ and length of the minor axis is ~1~ unit. Explain how the ellipse is reduced to a circle when its two foci coincide.

Solution.

The length of minor axis (2b)=1 \Rightarrow b=\frac 12

The distance between two foci is given by 

2ae=\sqrt{(1+1)^2}=2 \Rightarrow ae=1 \\ \text{or,}~~ a^2e^2=1 \\ \text{or,}~~ a^2\left(1-\frac{b^2}{a^2}\right)=1 \\ \text{or,}~~ a^2-b^2=1 \\ \text{or,}~~ a^2-\left(\frac 12\right)^2=1 \\ \text{or,}~~ a^2-\frac 14=1 \\ \text{or,}~~ a^2=1+\frac 14=\frac 54.

From the position of foci we can easily conclude that the ellipse will be of the form 

\frac{x^2}{b^2}+\frac{y^2}{a^2}=1 \\ \text{or,}~~ \frac{x^2}{\frac 14}+\frac{y^2}{\frac 54}=1 \\ \text{or,}~~ 4x^2+\frac 45 y^2=1 \\ \text{or,}~~ 20x^2+4y^2=5.

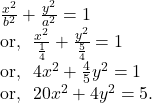
2nd Part :

When two foci coincide, then the distance between two foci (2ae)=0

\therefore~ e=0 \\ \text{or,}~~ \sqrt{1-\frac{b^2}{a^2}}=0 \\ \text{or,}~~ b=a.

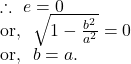
Hence, the equation of the ellipse is reduced into 

\frac{x^2}{a^2}+\frac{y^2}{a^2}=1 \Rightarrow x^2+y^2=a^2 \rightarrow(2)

So, the equation (2) represents a circle.

11.~ The eccentricity of an ellipse is ~\frac 12,~ focus is ~S(0,0)~ and the major axis and directrix intersect at ~Z(-1,-1).~ Find the co-ordinates of the centre of the ellipse.

Solution.

ellipse-s n dey

Let the centre of the ellipse be ~P(h,k). Now, the focus ~S(0,0)~ divides the line segment \overline{PZ} at the ratio ~ae :\left(\frac ae-ae\right) internally.

\therefore~ PS : SZ\\~~~=ae : \left(\frac ae-ae\right) \\~~~=ae:a\left(\frac 1e-e\right)\\~~~=e: \left(\frac 1e-e\right)\\~~~=\frac 12 :\left(2-\frac 12\right)\\~~~=\frac 12: \frac 32\\~~~=1:3 \\ \text{or,}~~ SZ:PS=3:1.

0=\frac{3h+(-1)}{3+1} \Rightarrow h=\frac 13, ~~ 0=\frac{3k+(-1)}{3+1} \Rightarrow k=\frac 13.

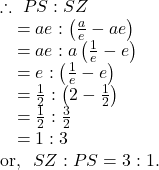
Hence, the centre of the ellipse is ~\left(\frac 13,\frac 13 \right).

12.~ The lengths of major and minor axes of an ellipse are ~8~ and ~6~ and their equations are ~y-1=0~ and ~x+3=0~ respectively. Find the equation of the ellipse.

Solution.

Since the major axis and minor axes are parallel to the ~x-axis and ~y-axis respectively. So, the equation of the ellipse can be taken in the form ~\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1~~(a^2>b^2),~ where ~(\alpha,\beta)~ is the centre of the ellipse.

The length of the major axis : 2a=8 \Rightarrow a=4.

The length of the major axis : 2b=6 \Rightarrow b=3.

Now, the centre of the ellipse is the intersection of ~y-1=0~ and ~x+3=0~ which is ~(-3,1).

Hence, the equation of the ellipse is 

\frac{(x+3)^2}{4^2}+\frac{(y-1)^2}{3^2}=1 \\ \text{or,}~~\frac{(x+3)^2}{16}+\frac{(y-1)^2}{9}=1.

13.~ Show that the point ~\left(2,\frac{2}{\sqrt{5}}\right)~ lies on the ellipse ~4x^2+5y^2=20.~ Show further that the sum of its distances from two foci is equal to the length of its major axis.

Solution.

\because~~4 \cdot 2^2+5 \cdot \left(\frac{2}{\sqrt{5}}\right)^2\\=16+5 \times \frac 45=16+4=20.

Since the point ~\left(2,\frac{2}{\sqrt{5}}\right)~ satisfies the equation of the ellipse, the point ~\left(2,\frac{2}{\sqrt{5}}\right)~ lies on the ellipse.

Again, ~4x^2+5y^2=20 \Rightarrow \frac{x^2}{5}+\frac{y^2}{4}=1

\therefore~ a^2=5,~~b^2=4.

So, ~e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac 45}=\sqrt{\frac{5-4}{5}}=\frac{1}{\sqrt{5}}.

Hence, the co-ordinates of the foci is 

(\pm ae,0)=\left(\pm \sqrt{5} \times \frac{1}{\sqrt{5}}\right)=(\pm 1,0).

So, the sum of its distances from the two foci is

=\sqrt{(2-1)^2+\left(\frac{2}{\sqrt{5}}-0\right)^2}+\sqrt{(2+1)^2+\left(\frac{2}{\sqrt{5}}-0\right)^2}\\=\sqrt{1+\frac 45}+\sqrt{9+\frac 45}\\=\sqrt{\frac 95}+\sqrt{\frac{49}{5}}\\=\frac{1}{\sqrt{5}}(3+7)\\=\frac{10}{\sqrt{5}}\\=2\sqrt{5}\\=2a=\text{the length of the major axis.}

14.~ Prove that ~SP+S'P=20~ for the ellipse ~\frac{x^2}{100}+\frac{y^2}{36}=1,~S~ and ~S'~ are two foci of the ellipse of the ellipse and ~P~ is any point on the ellipse.

Solution.

The equation of the given ellipse is ~\frac{x^2}{100}+\frac{y^2}{36}=1~ i.e., ~\frac{x^2}{10^2}+\frac{y^2}{6^2}=1 \rightarrow(1)

Comparing ~(1)~ with ~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1~, we get ~~a^2=10,~~y^2=6.

So, the co-ordinates of any point on the ellipse ~(1)~ can be written as ~(10\cos\theta,6\sin\theta).

\therefore~ e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{36}{100}}=\sqrt{\frac{64}{100}}=\frac{8}{10}=\frac 45.

So, the co-ordinates of the foci 

(\pm ae,0)=\left(\pm 10 \times \frac 45,0\right)=(\pm 8,0).

\therefore~ SP+S'P\\=\sqrt{(10\cos\theta-8)^2+(6\sin\theta)^2}+\sqrt{(10\cos\theta+8)^2+(6\sin\theta)^2}\\=\sqrt{100\cos^2\theta-160\cos\theta+64+36(1-\cos^2\theta)}\\~~+\sqrt{100\cos^2\theta+160\cos\theta+64+36(1-\cos^2\theta)}\\=\sqrt{10^2-2\cos 10\cdot 8\cos\theta+(8\cos\theta)^2}+\sqrt{10^2-2\cos 10\cdot 8\cos\theta+(8\cos\theta)^2}\\=(10-8\cos\theta)+(10+8\cos\theta)\\=20~~\text{(proved)}.

Post Views: 230

Leave a Comment