In the previous article , we solved few solutions of Short Answer Type Questions of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few long answer type questions.

1. Find ![]() the centre,
the centre, ![]() vertices,
vertices, ![]() equations of the axes,
equations of the axes, ![]() lengths of the axes,
lengths of the axes, ![]() eccentricity,
eccentricity, ![]() the length of latus rectum,
the length of latus rectum, ![]() co-ordinates of foci and
co-ordinates of foci and ![]() the equations of the directrices of each of the following ellipses :
the equations of the directrices of each of the following ellipses :
![]()
Solution (a).
We have the given equation of ellipse ![]()
Comparing ![]() with the general equation of ellipse
with the general equation of ellipse ![]() we get,
we get,
![]()
So, the major axis of the ellipse is parallel to the ![]() axis and minor axis is parallel to
axis and minor axis is parallel to ![]() -axis.
-axis.
(i) Centre ![]()
(ii) Vertex ![]() i.e.
i.e. ![]() and
and ![]()
(iii) Major axis is given by ![]() and minor axis is given by
and minor axis is given by ![]()
(iv) Length of major axis ![]() unit and length of minor axis
unit and length of minor axis ![]() unit.
unit.
(v) Eccentricity ![]()
(vi) Length of latus rectum ![]() unit.
unit.
(vii) The co-ordinates of foci are given by
![]()
i.e. ![]() and
and ![]()
(viii) The equation of the directrix is

Solution (b).
We have the given equation of ellipse ![]()
Comparing ![]() with the general equation of ellipse
with the general equation of ellipse ![]() we get,
we get,
![]()
Since ![]() the major axis of the ellipse is parallel to the
the major axis of the ellipse is parallel to the ![]() axis and minor axis is parallel to
axis and minor axis is parallel to ![]() -axis.
-axis.
(i) Centre ![]()
(ii) Vertex ![]() i.e.
i.e. ![]() and
and ![]()
(iii) Major axis is given by ![]() and minor axis is given by
and minor axis is given by ![]()
(iv) Length of major axis ![]() unit and length of minor axis
unit and length of minor axis ![]() unit.
unit.
(v) Eccentricity ![]()
(vi) Length of latus rectum ![]() unit.
unit.
(vii) The co-ordinates of foci are given by
![]()
i.e. ![]() and
and ![]()
For Full Solution PDF of the Ellipse ( S N De-Chhaya Mathematics ), click here.
Solution (c).
We have the given equation of ellipse

Comparing ![]() with the general equation of ellipse
with the general equation of ellipse ![]() we get,
we get,
![]()
Clearly, the major axis of the ellipse is parallel to the ![]() axis and minor axis is parallel to
axis and minor axis is parallel to ![]() -axis.
-axis.
(i) Centre ![]()
(ii) Vertex ![]() i.e.
i.e. ![]() and
and ![]()
(iii) Minor axis is given by ![]() and major axis is given by
and major axis is given by ![]()
(iv) Length of major axis ![]() unit and length of minor axis
unit and length of minor axis ![]() unit.
unit.
(v) Eccentricity ![]()
(vi) Length of latus rectum ![]() unit.
unit.
(vii)The co-ordinates of foci are given by
![]()
i.e. ![]() and
and ![]()
(viii) The equation of the directrix is

(viii) The equation of the directrix is

![]() Find the eccentricity, the lengths of latus rectum and the centre of the ellipse
Find the eccentricity, the lengths of latus rectum and the centre of the ellipse ![]()
Solution.
We have the given equation of ellipse

From ![]() we can say that the major axis of the given ellipse is parallel to
we can say that the major axis of the given ellipse is parallel to ![]() axis and minor axis of the ellipse is parallel to
axis and minor axis of the ellipse is parallel to ![]() axis.
axis.
The eccentricity of the ellipse is
![]()
The length of the latus rectum is
![]()
Finally, the centre of the ellipse is ![]()
![]() Find the latus rectum, the eccentricity and the co-ordinates of the foci of the ellipse
Find the latus rectum, the eccentricity and the co-ordinates of the foci of the ellipse ![]()
Solution.
The equation of the ellipse

Comparing ![]() with the general equation of ellipse
with the general equation of ellipse ![]() we get,
we get,
![]()
The length of the latus rectum
![]() .
.
The eccentricity of the ellipse is
![]()
The co-ordinates of foci are
![]()
i.e., ![]() and
and ![]()
i.e., ![]() and
and ![]() .
.
![]() Examine, with reasons, the validity of the following statement :
Examine, with reasons, the validity of the following statement :
![]() represents the equation of an ellipse whose eccentricity is
represents the equation of an ellipse whose eccentricity is ![]()
Solution.
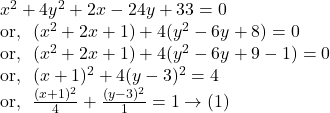
Comparing ![]() with the general equation of ellipse
with the general equation of ellipse ![]() we get,
we get, ![]() .
.
The eccentricity of ![]() is
is
![]()
So, the given equation represents the equation of the ellipse with eccentricity ![]()
Hence, the aforesaid statement is valid.