In the previous article , we have solved few Short Answer type questions of Hyperbola chapter of S.N.Dey mathematics, Class 11. In this article , we will solve few more Short Answer Type questions of Hyperbola related problems of s n dey mathematics class 11.

4(i) For what value of ![]() the hyperbola
the hyperbola ![]() will pass through the point
will pass through the point ![]() Find its eccentricity and the length of latus rectum.
Find its eccentricity and the length of latus rectum.
Solution.
Since the hyperbola ![]() passes through the point
passes through the point ![]() ,
,
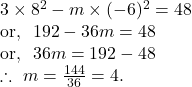
So, the equation of the given hyperbola is
![]()
Comparing ![]() with the general form of hyperbola
with the general form of hyperbola ![]() we get,
we get,
![]()
![]() The eccentricity
The eccentricity ![]() of the hyperbola is
of the hyperbola is
![]()
The length of the latus rectum is
![]()
(ii) The hyperbola ![]() passes through the point of intersection of the lines
passes through the point of intersection of the lines ![]() and its eccentricity is
and its eccentricity is ![]() ; show that its length of latus rectum is
; show that its length of latus rectum is ![]()
Solution.
![]()
So, from ![]() and
and ![]() we get,
we get,
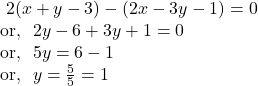
![]() By
By ![]() we get,
we get,
![]()
So, the point of intersection of ![]() and
and ![]() is
is ![]()
Since the hyperbola ![]() passes through the point
passes through the point ![]()


By ![]() we get,
we get,
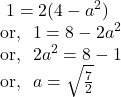
![]()
Hence, the length of its latus rectum is
![]()
Oswaal JEE Advance 10 Mock Test Papers (Paper-1 & Paper-2) Physics, Chemistry, Mathematics (For 2023 Exam) Paperback
(iii) The hyperbola ![]() passes through the point of intersection of the lines
passes through the point of intersection of the lines ![]() and
and ![]() and its latus rectum is
and its latus rectum is ![]() Find
Find ![]() and
and ![]() .
.
Solution.
![]()
From ![]() and
and ![]() we get,
we get,

From ![]() we get,
we get,
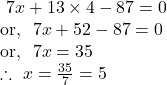
So, the point of intersection of the straight lines ![]() and
and ![]() is
is ![]()
Since the hyperbola ![]() passes through the point
passes through the point ![]()
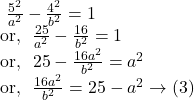
The length of latus rectum ![]()
By ![]() we get,
we get,
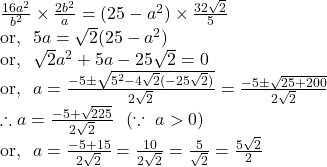
By ![]() we get,
we get,
![]()
(iv) The hyperbola ![]() passes through the point
passes through the point ![]() and its eccentricity is
and its eccentricity is ![]() find the length of its latus rectum.
find the length of its latus rectum.
Solution.
Since the hyperbola ![]() passes through the point
passes through the point ![]()


By ![]() we get,
we get,

From ![]() we get,
we get, ![]()
![]() the length of the latus rectum is
the length of the latus rectum is
![]()
5. Find the equation of the hyperbola whose.
(i) eccentricity is ![]() focus is
focus is ![]() and the directrix is the line
and the directrix is the line ![]()
Solution.
Let ![]() be any point on the hyperbola.
be any point on the hyperbola.
![]() The distance of
The distance of ![]() from the focus
from the focus ![]() is given by
is given by ![]()
Again, the distance of ![]() from the directrix
from the directrix ![]() is
is
![]()
![Rendered by QuickLaTeX.com \because~~ e=\frac 43, \\ \therefore~~ \frac{SP}{PM}=\frac 43 \\ \text{or,}~~ \frac{SP^2}{PM^2}=\left(\frac 43\right)^2=\frac{16}{9} \\ \text{or,}~~ 9 SP^2=16 PM^2 \\ \text{or,}~~ 9[x^2+(y-4)^2]=16 \times \frac{(4y-9)^2}{16} \\ \text{or,}~~ 9(x^2+y^2-8y+16)=16y^2-72y+81 \\ \text{or,}~~ 9x^2+9y^2-16y^2=81-144 \\ \text{or,}~~ 9x^2-7y^2=-63 \\ \text{or,}~~ 7y^2-9x^2=63.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-f494ca4fc2b2da8c6679bc8d7ff4e206_l3.png)
Xclusive JEE Advanced 45 Previous Year (1978 – 2022) Mathematics Chapterwise & Topicwise Solved Papers | IIT-JEE PYQ Question Bank in NCERT Flow with 100% Detailed Solutions for JEE 2023 Paperback
Product details
Publisher : AIETS.COM PVT. LTD. (1 January 2023)
Language : English
Paperback : 444 pages
ISBN-10 : 8119181220
ISBN-13 : 978-8119181223
Item Weight : 800 g
Country of Origin : India
(ii) eccentricity is ![]() focus is
focus is ![]() and directrix is the line
and directrix is the line ![]()
Solution.
Let ![]() be any point on the hyperbola.
be any point on the hyperbola.
![]() The distance of
The distance of ![]() from the focus
from the focus ![]() is given by
is given by ![]()
Again, the distance of ![]() from the directrix
from the directrix ![]() is
is
![]()
![Rendered by QuickLaTeX.com \because~ e=\frac 54 , \\ \therefore ~\frac{SP}{PM}=\frac 54 \\ \text{or,}~~ \frac{SP^2}{PM^2}=\left(\frac 54\right)^2=\frac{25}{16} \\ \text{or,}~~16 SP^2=25 PM^2 \\ \text{or,}~~ 16[(x+5)^2+y^2]=25 \times \frac{(5x+16)^2}{25} \\ \text{or,}~~ 16(x^2+10x+25+y^2)=25x^2+160x+256 \\ \text{or,}~~ 16x^2+160x+400+16y^2=25x^2+160x+256 \\ \text{or,}~~16x^2-25x^2+16y^2=256-400 \\ \text{or,}~~ -9x^2+16y^2=-144 \\ \text{or,}~~ 9x^2-16y^2=144 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-a41258382a4e182a0090b2dfbb6a52a5_l3.png)
Hence, the equation ![]() represents the required equation of hyperbola.
represents the required equation of hyperbola.
(iii)eccentricity is ![]() focus is
focus is ![]() and the equation of directrix is
and the equation of directrix is ![]()
Solution.
Let ![]() be any point on the hyperbola.
be any point on the hyperbola.
![]() The distance of
The distance of ![]() from the focus
from the focus ![]() is given by
is given by ![]()
Again, the distance of ![]() from the directrix
from the directrix ![]() is
is
![]()
![Rendered by QuickLaTeX.com \because~ e=\sqrt{3} , \\ \therefore ~~~\frac{SP}{PM}=\sqrt{3} \\ \text{or,}~~ \frac{SP^2}{PM^2}=\left(\sqrt{3}\right)^2 \\ \text{or,}~~ SP^2=3 PM^2 \\ \text{or,}~~ (x-2)^2+(y-3)^2=3 \times \frac{(x+2y-1)^2}{5} \\ \text{or,}~~5(x^2-4x+4+y^2-6y+9)\\=3[x^2+4y^2+1+2 \cdot x \cdot 2y+2 \cdot 2y \cdot(-1)+2 \cdot(-1) \cdot x] \\ \text{or,}~~ 5x^2-20x+20+5y^2-30y+45=3x^2+12y^2+3+12xy-12y-6x \\ \text{or,}~~2x^2-7y^2-12xy-14x-18y+62=0 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-53e3b4461cb93348c75480b67edf3623_l3.png)
Hence, the equation ![]() represents the required equation of hyperbola.
represents the required equation of hyperbola.
(iv) eccentricity is ![]() focus is
focus is ![]() and the equation of directrix is
and the equation of directrix is ![]()
Let ![]() be any point on the hyperbola.
be any point on the hyperbola.
![]() The distance of
The distance of ![]() from the focus
from the focus ![]() is given by
is given by ![]()
Again, the distance of ![]() from the directrix
from the directrix ![]() is
is
![]()

Hence, the equation ![]() represents the required equation of hyperbola.
represents the required equation of hyperbola.
(v) eccentricity is ![]() focus is
focus is ![]() and the equation of directrix is
and the equation of directrix is ![]()
Solution.
Let ![]() be any point on the hyperbola.
be any point on the hyperbola.
![]() The distance of
The distance of ![]() from the focus
from the focus ![]() is given by
is given by ![]()
Again, the distance of ![]() from the directrix
from the directrix ![]() is
is
![]()

Hence, the equation ![]() represents the required equation of hyperbola.
represents the required equation of hyperbola.
(vi) eccentricity is ![]() focus is
focus is ![]() and the equation of directrix is
and the equation of directrix is ![]()
Solution.
Let ![]() be any point on the hyperbola.
be any point on the hyperbola.
![]() The distance of
The distance of ![]() from the focus
from the focus ![]() is given by
is given by ![]()
Again, the distance of ![]() from the directrix
from the directrix ![]() is
is
![]()

Hence, the equation ![]() represents the required equation of hyperbola.
represents the required equation of hyperbola.
Read More :

