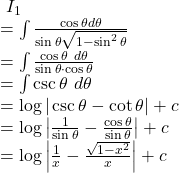Integration By Parts (Part-5)| S N Dey| Class 12

by

In the previous article, we have discussed the solutions of Short Answer type questions of Integration By Parts Chapter of S N Dey mathematics Class 12. In this chapter, we will discuss the problems of Short Answer Type Questions.

Integration By Parts, S N Dey Mathematics
Short Answer Type Questions of Integration By Parts | S N Dey

30.~~\displaystyle\int{\frac{\sin^{-1}x}{(1-x^2)^{3/2}}}~dx

Solution.

\displaystyle\int{\frac{\sin^{-1}x}{(1-x^2)^{3/2}}}~dx\\=\int{\frac{\sin^{-1}x}{(1-x^2)\sqrt{1-x^2}}~dx}\rightarrow(1)

\text{let}~\sin^{-1}x=z \\ \therefore~ \frac{1}{\sqrt{1-x^2}}~dx=dz \rightarrow(2)

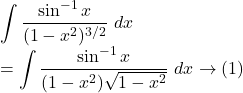
Hence, from ~(1),~(2)~ we get,

\displaystyle\int{\frac{\sin^{-1}x}{(1-x^2)\sqrt{1-x^2}}}~dx\\=\int{\frac{z}{1-\sin^2z}}~dz\\=\int{\frac{z}{\cos^2z}}~dz\\=\int{z\sec^2z}~dz\\=z\int{\sec^2z}~dz-\int{\left[\frac{d}{dz}(z)\int{\sec^2z}~dz\right]}~dz\\=z\tan z-\int{\tan z}~dz\\=z\tan z-\log|\sec z|+c\\=z\left(\frac{\sin z}{\cos z}\right)-\log\left|\frac{1}{\cos z}\right|+c\\=\sin^{-1}x~\left(\frac{x}{\sqrt{1-x^2}}\right)-\log\left|\frac{1}{\sqrt{1-x^2}}\right|+c\\=\sin^{-1}x~\left(\frac{x}{\sqrt{1-x^2}}\right)+\frac 12\log|1-x^2|+c.

31.~~ \displaystyle\int{\frac{x}{1+\sin x}}~dx

Solution.

\displaystyle\int{\frac{x}{1+\sin x}}~dx\\=\int{\frac{x(1-\sin x)}{(1+\sin x)(1-\sin x)}}~dx\\=\int{\frac{x(1-\sin x)}{1-\sin^2x}}~dx\\=\int{\frac{x}{\cos^2x}}~dx-\int{\frac{x\sin x}{\cos^2x}}~dx\\=\int{x\sec^2x}~dx-\int{x~\sec x\tan x}~dx\\=I_1-I_2.

I_1\\=x\int{\sec^2x}~dx-\int{\left[\frac{d}{dx}(x)\int{\sec^2x}~dx\right]}~dx\\=x\tan x-\int{1 \cdot \tan x}~dx\\=x\tan x-\log|\sec x|+c_1.

I_2\\=\int{x~\sec x\tan x}~dx\\=x\int{\sec x\tan x}~dx-\int{\left[\frac{d}{dx}(x)\int{\sec x\tan x}~dx\right]}~dx\\=x\sec x-\int{\sec x}~dx\=x\sec x-\log|\sec x+\tan x|+c_2.

\therefore~ \displaystyle\int{\frac{x}{1+\sin x}}~dx\\=(x\tan x-\log|\sec x|+c_1)-(x\sec x-\log|\sec x+\tan x|+c_2)\\=x\tan x-\log|\sec x|-x\sec x+\log|\sec x+\tan x|+c.[*]\\=x(\tan x-\sec x)+\log|\cos x|+\log|\sec x+\tan x|+c.

Note [*] : ~~~~[~c=c_1-c_2~]

32.~~\displaystyle\int{\frac{x-\sin x}{1-\cos x}}~dx

Solution.

~\displaystyle\int{\frac{x-\sin x}{1-\cos x}}~dx\\=\int{\frac{x-\sin x}{2\sin^2(x/2)}}~dx\\=\frac 12\int{x\csc^2(x/2)}~dx-\int{\frac{2\sin(x/2)\cos(x/2)}{2\sin^2(x/2)}}~dx\\=\frac 12I_1-\int{\cot(x/2)}~dx\rightarrow(1)

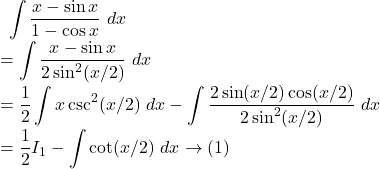
I_1\\=\displaystyle\int{x\csc^2(x/2)}~dx\\=x\int{\csc^2(x/2)}~dx-\int{\left[\frac{d}{dx}(x)\int{\csc^2(x/2)}~dx\right]}~dx\\=x \left(-\frac{\cot(x/2)}{1/2}\right)-\int{\left(-\frac{\cot(x/2)}{1/2}\right)}~dx\\=-2x\cot(x/2)+2\int{\cot(x/2)}~dx+c_1 \rightarrow(2)

Hence, by ~(1),~(2)~ we get,

~\displaystyle\int{\frac{x-\sin x}{1-\cos x}}~dx\\=\frac 12\left[-2x\cot(x/2)+2\int{\cot(x/2)}~dx+c_1\right]-\int{\cot(x/2)}~dx\\=-x\cot(x/2)+\int{\cot(x/2)}~dx-\int{\cot(x/2)}~dx+c~~[c=c_1/2]\\=-x\cot(x/2)+c.

33.~~\displaystyle\int{\sin x \log(\sec x+\tan x)}~dx

Solution.

\displaystyle\int{\sin x \log(\sec x+\tan x)}~dx\\=\log(\sec x+\tan x)\int{\sin x}~dx-\int{\left[\frac{d}{dx}(\log(\sec x+\tan x))\int{\sin x}~dx\right]}~dx\\=-\cos x\log(\sec x+\tan x)-\int{\frac{\sec x\tan x+\sec^2x}{(\sec x+\tan x)}\cdot (-\cos x)}~dx\\=-\cos x\log(\sec x+\tan x)+\int{\cos x \cdot \frac{\sec x(\sec x+\tan x)}{(\sec x+\tan x)}}~dx\\=-\cos x\log(\sec x+\tan x)+\int{dx}+c\\=-\cos x\log(\sec x+\tan x)+x+c.

34.~~ \displaystyle\int{\cos x\log(\csc x+\cot x)}~dx

Solution.

\displaystyle\int{\cos x\log(\csc x+\cot x)}~dx\\=\log(\csc x+\cot x) \int{\cos x}~dx-\int{\left[\frac{d}{dx}(\log(\csc x+\cot x))\int{\cos x}~dx\right]}~dx\\=\log(\csc x+\cot x) \cdot \sin x-\int{\frac{-\csc x\cot x-\csc^2x}{\csc x+\cot x}\cdot (\sin x)}~dx\\=\sin x \log(\csc x+\cot x)+\int{\frac{\csc x(\csc x+\cot x)}{(\csc x+\cot x)} \cdot (\sin x)}~dx\\=\sin x \log(\csc x+\cot x)+\int{dx}\\=\sin x \log(\csc x+\cot x)+x+c.

35.~~ \displaystyle\int{\tan^{-1}\sqrt{x}}~dx

Solution.

\displaystyle\int{\tan^{-1}\sqrt{x}}~dx\\= \tan^{-1}\sqrt{x}\int{dx}-\int{\left[\frac{d}{dx}(\tan^{-1}\sqrt{x})\int{dx}\right]}~dx\\=x\tan^{-1}\sqrt{x} -\int{\frac{1}{1+(\sqrt{x})^2} \cdot \frac{1}{2\sqrt{x}} \cdot x}~dx\\=x\tan^{-1}\sqrt{x}-\frac 12 \int{\frac{\sqrt{x}}{1+x}}~dx\rightarrow(1)

~\text{let}~x=\tan^2\theta \ \therefore~dx=2\tan\theta\sec^2\theta~d\theta \rightarrow(2)

So, by ~(1),~(2)~ we get,

\displaystyle\int{\tan^{-1}\sqrt{x}}~dx\\=x\tan^{-1}\sqrt{x}-\frac 12 \int{\frac{\tan\theta}{1+\tan^2\theta} \cdot (2\tan \theta \sec^2\theta)}~d\theta\\=x\tan^{-1} \sqrt{x}-\int{\frac{\tan \theta}{\sec^2\theta} \times \tan\theta \sec^2\theta}~d\theta\\=x\tan^{-1} \sqrt{x}-\int{\tan^2\theta }~d\theta \\=x\tan^{-1} \sqrt{x}-\int{(\sec^2\theta -1)}~d\theta\\=x\tan^{-1} \sqrt{x}-\int{\sec^2\theta }~d\theta +\int{d\theta } \\=x\tan^{-1} \sqrt{x}-\tan\theta +\theta +c.\\=x\tan^{-1} \sqrt{x}-\sqrt{x}+\tan^{-1} \sqrt{x}+c\\=(x+1) \tan^{-1} \sqrt{x}-\sqrt{x}+c.

36.~~\displaystyle\int{x\sin x \sin 2x}~dx

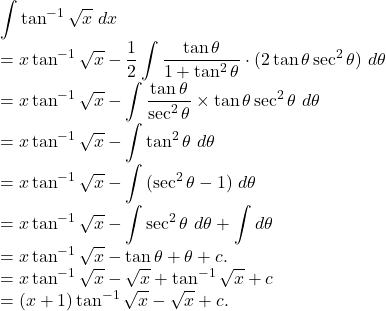
Solution.

\displaystyle\int{x\sin x \sin 2x}~dx\\=\frac 12\int{x(2\sin x\sin2x)}~dx\\=\frac 12\displaystyle\int{x(\cos x-\cos 3x)}~dx\\=\frac 12\int{x \cos x}~dx-\frac 12 \int{x \cos3x}~dx\\=\frac 12(I_1-I_2)

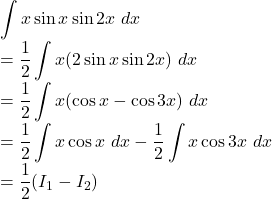
~I_1\\=\displaystyle\int{x \cos x}~dx\\=x\int{\cos x}~dx- \int{\left[\frac{d}{dx}(x)\int{\cos x}~dx\right]}~dx\\=x\sin x-\int{1\cdot \sin x}~dx\\=x\sin x+\cos x

~I_2\\=\displaystyle\int{x \cos 3x}~dx\\=x\int{\cos 3x}~dx- \int{\left[\frac{d}{dx}(x)\int{\cos 3x}~dx\right]}~dx\\=\frac 13x\sin 3x-\frac 13\int{1\cdot \sin 3x}~dx\\=\frac{x\sin3x}{3}+\frac 13 \cdot \frac 13(\cos 3x)

\therefore~\displaystyle\int{x\sin x \sin 2x}~dx\\=\frac 12 x\sin x+\frac 12 \cos x-\frac 16 x \sin 3x-\frac{1}{18}(\cos3x)+c.

37.~~ \displaystyle\int{x \tan x \sec^2 x}~dx

Solution.

\displaystyle\int{x \tan x \sec^2 x}~dx\\=x\int{\tan x}~d(\tan x)-\int{\left[\frac{d}{dx}(x)\int{\tan x}~d(\tan x)\right]}~dx\\~~[\because~d(\tan x)=\sec^2x~dx]\\=x\left(\frac{\tan^2x}{2}\right)-\int{1 \cdot \frac{\tan^2x}{2}}~dx\\=\frac x2 \cdot \tan^2x-\frac 12 \int{(\sec^2x-1)}~dx\\=\frac x2 \cdot \tan^2x-\frac 12 \int{\sec^2x~dx}+\frac 12 \int{dx}\\=\frac{x\tan^2x}{2}-\frac 12 \tan x+\frac x2+c.\\=\frac x2(\tan^2x+1)-\frac 12 \tan x+c\\=\frac x2~\sec^2x-\frac 12 \tan x+c\\=\frac 12(x \sec^2x-\tan x)+c.

38.~~ \displaystyle\int{\frac{\sin^{-1}x}{x^2}}~dx

Solution.

\displaystyle\int{\frac{\sin^{-1}x}{x^2}}~dx\\=(\sin^{-1}x) \int{\frac{dx}{x^2}}-\int{\left[\frac{d}{dx}(\sin^{-1}x)\int{\frac{dx}{x^2}}\right]}~dx\\=\sin^{-1}x \cdot \frac{x^{-2+1}}{-2+1}- \int{\frac{1}{\sqrt{1-x^2}} \cdot \frac{x^{-2+1}}{-2+1}}\\=-\sin^{-1}x \cdot x^{-1}+ \int{\frac{1}{x\sqrt{1-x^2}}}~dx\\=-\frac{\sin^{-1}x}{x}+I_1.

I_1= \int{\frac{1}{x\sqrt{1-x^2}}}~dx \rightarrow(1)

\text{let}~~x=\sin\theta \ \therefore~ dx=\cos\theta d\theta \rightarrow(2)

Hence, by ~(1),~(2)~ we get,

~I_1\\=\int{\frac{\cos\theta d\theta }{\sin \theta \sqrt{1-\sin^2\theta}}}\\=\int{\frac{\cos \theta~d\theta}{\sin \theta \cdot \cos \theta}} \\=\int{\csc \theta}~d\theta\\=\log|\csc \theta-\cot \theta|+c\\=\log\left|\frac{1}{\sin\theta}-\frac{\cos \theta}{\sin \theta}\right|+c\\=\log \left|\frac 1x-\frac{\sqrt{1-x^2}}{x}\right|+c\=\log \left|\frac{1-\sqrt{1-x^2}}{x}\right|+c

~\therefore~ \displaystyle\int{\frac{\sin^{-1}x}{x^2}}~dx=-\frac{\sin^{-1}x}{x}+\log \left|\frac{1-\sqrt{1-x^2}}{x}\right|+c.

Post Views: 188

Leave a Comment