Plane | Part-1 | Ex-5B Examhoop

In the following article, we are going to discuss/solve MCQ Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Plane (Ex-5B). In the previous article , we have solved few Short Answer type Questions.

*Plane-Ex-5B-S N De MCQ Complete Solution*

Choose the correct option:

1. The distance of the point $~(1,0,-3)~$ from the plane $~x-y-z=9~$ measured parallel to the line $~\frac{x-2}{2}=\frac{y+2}{3}=\frac{z-6}{-6}~$ is-

$(a)~9~~(b)~5~~(c)~7~~(d)~\text{none of these}$

Solution.

The equation of the straight line passing through the point $~(1,0,-3)~$ and parallel to the line $~\frac{x-2}{2}=\frac{y+2}{3}=\frac{z-6}{-6}~$ is

$~\frac{x-1}{2}=\frac{y-0}{3}=\frac{z+3}{-6}~=\lambda~(\neq 0,\text{say}) \\ ~~~~~\therefore~~ x=2\lambda+1,~y=3\lambda,~z=-6\lambda-3.$

So, the point $~(2\lambda+1,3\lambda,-6\lambda-3)~$ lies on the plane $~x-y-z=9.$

$\therefore~ (2\lambda+1)-3\lambda-(-6\lambda-3)=9 \\~~~~~ \text{or,}~~ 2\lambda+1-3\lambda+6\lambda+3=9 \\~~~~~ \text{or,}~~ 5\lambda=9-4 \\~~~~~ \therefore~ \lambda=\frac 55=1.$

$\therefore~$ The point on the plane is $~(2 \times 1+1, 3 \times 1,-6 \times 1-3)=(3,3,-9).$

So, the required distance is

$\sqrt{(3-1)^2+(3-0)^2+(-9+3)^2}=\sqrt{4+9+36}=\sqrt{49}=7~\text{unit}$

So, option (c) is correct.

$2.$ The angle between the line $~\vec{r}=(\hat{i}+2\hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})~$ and the plane $~\vec{r} \cdot (2\hat{i}-\hat{j}+\hat{k})=4~$ is –

$(a)~\cos^{-1}\frac 13~~(b)~\cos^{-1}\frac{1}{\sqrt{3}}~~(c)~0~~(d)~\sin^{-1}\frac 13.$

Solution.

We know that if $~\theta~$ is the angle between a line $~\vec{r}=\vec{a}+\lambda \vec{b}~$ and the plane $~ \vec{r} \cdot \vec{n}=d,~$ then $~\sin\theta=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\longrightarrow(1)$

Here, $~\vec{b}=\hat{i}-\hat{j}+\hat{k}~;~ \vec{n}=2\hat{i}-\hat{j}+\hat{k}$

$\therefore~~ \vec{b} \cdot \vec{n}=(\hat{i}-\hat{j}+\hat{k}) \cdot (2\hat{i}-\hat{j}+\hat{k})=2+1+1=4.$

$\text{Also,}~~|\vec{b}|=\sqrt{1^2+(-1)^2+1^2}=\sqrt{3},\\~~~~|\vec{n}|=\sqrt{2^2+(-1)^2+1^2}=\sqrt{4+1+1}=\sqrt{6}. \\ ~~~~~\therefore~~ |\vec{b}||\vec{n}|=\sqrt{3} \times \sqrt{6}=\sqrt{18}=3\sqrt{2}. \\ ~~~~~\sin\theta=\frac{4}{3\sqrt{2}}=\frac{2 \times 2}{3\sqrt{2}}=\frac{2\sqrt{2}}{3} \Rightarrow \theta=\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$

$\because ~~\sin^2\theta+\cos^2\theta=1 \\ ~~~~~\text{or,}~~ \left(\frac{2\sqrt{2}}{3}\right)^2+\cos^2\theta=1\\~~~~~ \text{or,}~~ \frac 89+\cos^2\theta=1 \\~~~~~ \text{or,}~~ \cos\theta=\sqrt{1-\frac 89}=\frac 13 \\ ~~~~~\therefore~~ \theta=\cos^{-1}\frac 13.$

So, option (a) is correct.

$3.~$ The distance between the parallel planes $~x+2y-2z-1=0~$ and $~2x+4y-4z+5=0~$ is-

$~(a)~1~\text{unit}~~(b)~\frac 67~~\text{units}~~(c)~\frac 76~~\text{units}~~(d)~\frac 57~~\text{units}$

Solution.

Two parallel planes are given by

$x+2y-2z-1=0 \longrightarrow(1),~~x+2y-2z+\frac 52=0 \longrightarrow(2).$

So, the distance $~(d)~$ between (1) and (2) is

$=\frac{\left|-1-\frac 52\right|}{\sqrt{1^2+2^2+(-2)^2}}=\frac{|-7/2|}{\sqrt{9}}=\frac 76~~\text{units}$

Hence, option (c) is correct.

MTG 35 Years NEET Previous Year Solved Question Papers with NEET Chapterwise Topicwise Solutions – NEET 2023 Preparation Books, Set of 3 Books NTA Neet 35 Years Questions, Physics Chemistry Biology Paperback –

$4.~$ The equation of the image of the line $~\frac{x-1}{9}=\frac{y-2}{-1}=\frac{z+3}{-3}~$ in the plane $~3x-3y+10z-26=0~$ is-

$~(a)~~\frac{2x-5}{18}=\frac{2y-1}{2}=\frac{z-2}{3}~~(b)~\frac{2x-5}{18}=\frac{2y+1}{-2}=\frac{z-2}{3}\\~~~~~~(c)~ \frac{2x+5}{18}=\frac{2y-1}{2}=\frac{z-2}{-3}~~~(d)~ \frac{2x-5}{18}=\frac{2y-1}{-2}=\frac{z-2}{-3}~$

Solution.

The equation of the straight line passing through the point $~P(1,2,-3)~$ and with direction ratios $~3,-3,10~$ is given by

$\frac{x-1}{3}=\frac{y-2}{-3}=\frac{z+3}{10}=\lambda (\neq 0,\text{say}) \\ \therefore~~ x=3\lambda+1,~~y=-3\lambda+2,~z=10\lambda-3.$

So, the point $~Q~(3\lambda+1,-3\lambda+2,~10\lambda-3)~$ lies on the plane $~3x-3y+10z-26=0.$

$\therefore~~3(3\lambda+1)-3(-3\lambda+2)+10(10\lambda-3)-26=0 \\~~~~ \text{or,}~~ 9\lambda+3+9\lambda-6+100\lambda-30-26=0 \\ ~~~~\text{or,}~~ 118\lambda-59=0 \Rightarrow \lambda=\frac{59}{118}=\frac 12.$

$\therefore~~ Q \equiv \left(3 \cdot \frac 12+1,-3 \cdot \frac 12+1,10 \cdot \frac 12-3\right)=\left(\frac 52,\frac 12,2\right).$

Let $~R(x,y,z)~$ be the image of the point $~P.$

$\therefore~ Q~$ is the midpoint of the line $~PR$ .

$\therefore~~\left(\frac{1+x}{2},\frac{2+y}{2},\frac{z-3}{2}\right)=\left(\frac 52,\frac 12,2\right) \\ \therefore~~ \frac{1+x}{2}=\frac 52 \Rightarrow x=4,~~\frac{2+y}{2}=\frac 12 \Rightarrow y=-1,~~ \frac{z-3}{2}=2 \Rightarrow z=7.$

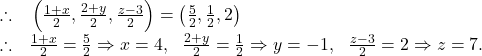
So, the image of the given straight line through the point $~(4,-1,7)~$ is

$\frac{x-4}{9}=\frac{y+1}{-1}=\frac{z-7}{-3}~;$

Also, the image of the given straight line through the point $~\left(\frac 52,\frac 12,2\right)~$ is

$\frac{x-\frac 52}{9}=\frac{y-\frac 12}{-1}=\frac{z-2}{-3}\Rightarrow \frac{2x-5}{18}=\frac{2y-1}{-2}=\frac{z-2}{-3}.$

So, option (d) is correct.

Read More : Complete S N Dey Solution of Plane (Ex-5A) Chapter with PDF link

5. The coordinates of the foot of perpendicular from $~(7,14,5)~$ to the plane $~2x+4y-z=2~$ is-

$~(a)~(-1,-2,-8)~~(b)~(1,2,8)~~(c)~(1,-2,8)~~(d)~(1,2,-8)$

Solution.

The equation of the straight line passing through the point $~(7,14,5)~$ and with direction ratios $~~2,4,-1~$ is given by

$~\frac{x-7}{2}=\frac{y-14}{4}=\frac{z-5}{-1}=\lambda ~(\neq 0, \text{say}) \\~~~ \therefore~~ x=2\lambda+7,~~y=4\lambda+14,~~z=-\lambda+5.$

So, the point $~(2\lambda+7,4\lambda+14,-\lambda+5)~$ lies on the plane $~2x+4y-z=2.$

$\therefore~~ 2(2\lambda+7)+4(4\lambda+14)-(-\lambda+5)=2 \\ ~~~~\text{or,}~~ 4\lambda+14+16\lambda+56+\lambda-5=0 \\~~~~ \text{or,}~~ 21\lambda+63=0 \\~~~~ \text{or,}~~ \lambda=-\frac{63}{21}=-3.$

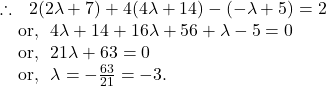
So, the required point is $~~(2 \times (-3)+7, 4 \times (-3)+14,~-(-3)+5)=(1,2,8).$

So, option (b) is correct.

6. State which of the following statement is true ?

(a) The distance between the line $~\vec{r}=(2 \hat{i}-2 \hat{j}+3 \hat{k})+\lambda( \hat{i}- \hat{j}+4 \hat{k})~$ and the plane $~\vec{r} \cdot ( \hat{i}+5 \hat{j}+ \hat{k})=5~$ is $~\frac{10}{3\sqrt{3}}~$ units.

(b) Distance between the parallel planes $~\vec{r} \cdot (2 \hat{i}- \hat{j}+3 \hat{k})+13=0~$ is $~7~$ units.

(d) The distance of a point $~(2,5,-3)~$ from the plane $~\vec{r} \cdot (6 \hat{i}-3 \hat{j}+2 \hat{k})=4~$ is $~\frac{7}{13}~$ units.

Explanation.

Applying the rule $~p=\frac{|\vec{a} \cdot \vec{n}-d|}{|\vec{n}|},~~$ where $~\vec{a}=2\hat{i}-2\hat{j}+3\hat{k},~~ \vec{n}=\hat{i}+5\hat{j}+\hat{k},~d=5,~~$ we get, the required distance

$=\frac{|(2\hat{i}-2\hat{j}+3\hat{k}) \cdot (\hat{i}+5\hat{j}+\hat{k})-5|}{|\hat{i}+5\hat{j}+\hat{k}|}=\frac{|2-10+3-5|}{\sqrt{1^2+5^2+1^2}}=\frac{1}{\sqrt{27}} \times 10=\frac{10}{3\sqrt{3}}~~\text{units}$

So, option (a) is correct.

MTG Objective NCERT at your FINGERTIPS – Chemistry, Best Books for NEET & JEE Preparation (Based on NCERT Pattern – Latest & Revised Edition 2022) Paperback

7. The foot of the perpendicular from the point $~(1,1,2)~$ to the plane $~2x-2y+4z+5=0~$ is-

$(a)~\left(\frac{1}{12},\frac{25}{12},\frac{2}{12}\right)~~ (b)~\left(-\frac{1}{12},\frac{25}{12},-\frac{2}{12}\right)~~ (c)~\left(\frac{1}{12},\frac{25}{12},-\frac{2}{12}\right)~~ (d)~\text{none of these}~~$

Solution.

By question, the equation of the straight line can be written as

$~\frac{x-1}{2}=\frac{y-1}{-2}=\frac{z-2}{4}=\lambda( \neq 0, \text{say}), \\ \therefore~~ x=2\lambda+1,~y=-2\lambda+1,~z=4\lambda+2.$

Clearly, the point $~(2\lambda+1,-2\lambda+1,4\lambda+2)~$ lies on the plane $~2x-2y+4z+5=0.$

$\therefore~~2(2\lambda+1)-2(-2\lambda+1)+4(4\lambda+2)+5=0 \\~~~~ \text{or,}~~ 4\lambda+2+4\lambda-2+16\lambda+8+5=0 \\ ~~~~\text{or,}~~ 24\lambda=-13 \Rightarrow \lambda=-\frac{13}{24}.$

Hence, the foot of the perpendicular from the point $~(1,1,2)~$ to the given plane is

$~\left(2 (-\frac{13}{24})+1, -2(-\frac{13}{24})+1,4(-\frac{13}{24})+2\right)\\~~~~=\left(-\frac{13}{12}+1, \frac{13}{12}+1,-\frac{13}{6}+2\right)\\~~~~=\left(-\frac{1}{12},\frac{25}{12},-\frac 16\right).$

$\therefore~$ option (b) is correct.

8. The vector equation of the plane passing through the origin and the line of intersection of the planes $~\vec{r} \cdot \vec{a}=\lambda~$ and $~\vec{r} \cdot \vec{b}=\mu~$ is-

$~(a)~\vec{r} \cdot (\lambda \vec{a}-\mu \vec{a})=0~~(b)~\vec{r} \cdot (\lambda \vec{b}-\mu \vec{a})=0~~ (c)~\vec{r} \cdot (\lambda \vec{a}+\mu \vec{a})=0~~ (d)~\vec{r} \cdot (\lambda \vec{b}+\mu \vec{a})=0$

Solution.

The vector equation of the plane passing through the origin and the line of intersection of the planes $~\vec{r} \cdot \vec{a}=\lambda~$ and $~\vec{r} \cdot \vec{b}=\mu~$ is

$(\vec{r} \cdot \vec{a}-\lambda)+t(\vec{r} \cdot \vec{b}-\mu)=0,~$ where $~t~$ is any non-zero finite number.

$\therefore~~\vec{r} \cdot (\vec{a}+t \vec{b})=\lambda+\mu t\longrightarrow(1)$

Since the plane (1) passes through the origin, $~\lambda+\mu t=0 \Rightarrow t=-\frac{\lambda}{\mu}.$

So, by (1) we get,

$\vec{r} \cdot \left(\vec{a}-\frac{\lambda}{\mu} \cdot \vec{b}\right)=0 \\ \text{or,}~~ \vec{r} \cdot (\lambda \vec{b}-\mu \vec{a})=0.$

Hence, option (b) is correct .

9. Value of $~\lambda~$ such that the line $~\frac{x-1}{2}=\frac{y-1}{3}=\frac{z-1}{\lambda}~$ is perpendicular to normal to the plane $~\vec{r} \cdot (2\hat{i}+3\hat{j}+4\hat{k})=0~$ is-

$~(a)~ -\frac{13}{4}~~(b)~-\frac{17}{4}~(c)~4~~(d)~-\frac{11}{4}$

Explanation.

By question, $~~ 2 \cdot 2+ 3 \cdot 3+ 4\cdot \lambda=0 \Rightarrow \lambda=-\frac{13}{4}.$

So, option (a) is correct.

10. The angle between $~\hat{i}~$ and line of intersection of the planes $~\vec{r} \cdot (\hat{i}+2\hat{j}+3\hat{k})=0~$ and $~\vec{r} \cdot (3\hat{i}+3\hat{j}+\hat{k})=0~$ is-

$(a)~ \cos^{-1} \frac 13~~(b)~\cos^{-1}\frac{1}{\sqrt{3}}~~(c)~\cos^{-1}\frac{2}{\sqrt{3}}~~(d)~\cos^{-1}\frac{7}{\sqrt{122}}$

Solution.

Given planes are $~\vec{r} \cdot \vec{n_1}=0,~~\vec{r} \cdot \vec{n_2}=0~~$ where $~\vec{n_1}=\hat{i}+2\hat{j}+3\hat{k},~\vec{n_2}=3\hat{i}+3\hat{j}+\hat{k}.$

$\therefore~~\vec{n}=\vec{n_1} \times \vec{n_2}=\begin{vmatrix} \hat{i}&\hat{j} &\hat{k} \\ 1& 2 &3 \\ 3& 3 &1 \\ \end{vmatrix} \\ \text{or,}~~ \vec{n}=\hat{i}(2-9)-\hat{j}(1-9)+\hat{k}(3-6)=-7\hat{i}+8\hat{j}-3\hat{k}.$

If $~\theta~$ is the angle between $~\hat{i}~$ and $~\vec{n}~$ , then

$\cos\theta=\frac{|-7|}{\sqrt{(-7)^2+8^2+(-3)^2}}=\frac{7}{\sqrt{122}} \\ \text{or,}~~ \theta=\cos^{-1} \left(\frac{7}{\sqrt{122}}\right)$

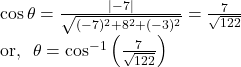
So, option (d) is correct.

11. The acute angle between the planes $~2x-y+z=6~$ and $~x+y+2z=3~$ is-

$~(a)~45^{\circ}~~(b)~60^{\circ}~~(c)~30^{\circ}~~(d)~75^{\circ}$

Explanation.

If $~\theta~$ be the acute angle between two given planes, then

$~\cos\theta=\frac{2 \cdot 1+(-1) \cdot 1+1 \cdot 2}{\sqrt{2^2+(-1)^2+1^2} \sqrt{1^2+1^2+2^2}}=\frac{2-1+2}{\sqrt{6} \sqrt{6}} \\ \therefore~\cos\theta=\frac{3}{\sqrt{6 \times 6}}=\frac 36 \\ \text{or,}~~ \theta=\cos^{-1}\left(\frac 12\right)=60^{\circ}.$

So, option (b) is correct.

12. The angle between the line $~\frac{x-1}{2}=\frac{y-2}{1}=\frac{z+3}{-1}$ and the plane $~x+y+4=0~$ is-

$~(a)~45^{\circ}~~(b)~60^{\circ}~~(c)~30^{\circ}~~(d)~75^{\circ}$

Explanation.

If $~\theta~$ be the angle between the line $~\frac{x-1}{2}=\frac{y-2}{1}=\frac{z+3}{-1}~$ and the plane $~x+y+4=0~$ , then

$~\sin\theta=\frac{2 \cdot 1+1 \cdot 1+ (-1) \cdot 0}{\sqrt{2^2+1^2+(-1)^2} \sqrt{1^2+1^2+0^2}}=\frac{2+1}{\sqrt{6}\sqrt{2}} \\ \text{or,}~~ \sin\theta=\frac{3}{\sqrt{12}}=\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2} \\ \therefore~ \theta=60^{\circ}.$

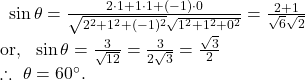
So, option (b) is correct.

Post Views: 49

In the following article, we are going to discuss/solve MCQ Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Plane (Ex-5B). In the previous article , we have solved few Short Answer type Questions.

Read More : Complete S N Dey Solution of Plane (Ex-5A) Chapter with PDF link

Leave a Comment Cancel reply