Plane | Part-2 | Ex-5B

by
In the previous article , we have solved complete MCQ of Plane Chapter (Ex-2B) of S N De Mathematics(Chhaya). In the following article, we are going to discuss/solve VSA (Very Short Answer) Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Plane (Ex-5B).
Plane | Part-2 | Ex-5B-S N De Mathematics Solutions
Plane | Part-2 | Ex-5B-S N De Mathematics Solutions

1. Find the angle between the line ~\vec{r}=(\hat{i}+2\hat{j}-\hat{k})+t(\hat{i}-\hat{j}+\hat{k})~ and the plane ~\vec{r} \cdot (2\hat{i}-\hat{j}+\hat{k})=4.

Solution.

We know that if ~\theta~ be the angle between  a line ~\vec{r}=\vec{a}+t\vec{b}~ and the plane ~\vec{r} \cdot \vec{n}=d,~ then ~\sin\theta=\frac{\vec{b}\cdot \vec{n}}{|\vec{b}||\vec{n}|}\longrightarrow(1)

Here, ~\vec{b}=\hat{i}-\hat{j}+\hat{k},~~\vec{n}=2\hat{i}-\hat{j}+\hat{k}.

\therefore~ By (1), we get

~\sin\theta=\frac{(\hat{i}-\hat{j}+\hat{k}) \cdot (2\hat{i}-\hat{j}+\hat{k})}{|\hat{i}-\hat{j}+\hat{k}| |2\hat{i}-\hat{j}+\hat{k}|}=\frac{2+1+1}{\sqrt{1^2+(-1)^2+1^2} \sqrt{2^2+(-1)^2+1^2}} \\~~~ \text{or,}~~ \sin\theta=\frac{4}{\sqrt{3}\sqrt{6}}=\frac{4}{3\sqrt{2}} \\~~~ \therefore~~\sin\theta=\frac{2\sqrt{2}}{3} \Rightarrow \theta=\sin^{-1} \left(\frac{2\sqrt{2}}{3}\right)

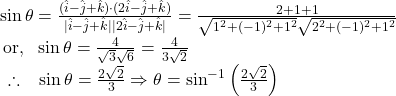
2. Obtain the equation of the plane passing through the point ~(1,-3,-2)~ and perpendicular to the planes ~x+2y+2z=5~ and ~3x+3y+2z=8. [CBSE-’09]

Solution.

Let the direction ratios of the normal to the plane (to be determined) be ~a,b,c.

\therefore~~ a+2b+2c=0 \longrightarrow(1),~~3a+3b+2c=0 \longrightarrow(2) 

So, from (1) and (2) we get by cross-multiplication,

~\frac{a}{4-6}=\frac{b}{6-2}=\frac{c}{3-6} \Rightarrow \frac{a}{-2}=\frac{b}{4}=\frac{c}{-3}.

Since the plane passes through the point ~(1,-3,-2)~ and perpendicular to the given planes , the equation of the plane can be written as 

~-2(x-1)+4(y+3)-3(z+2)=0 \\~~~ \text{or,}~~ -2x+2+4y+12-3z-6=0 \\~~~ \text{or,}~~ -2x+4y-3z+8=0 \\~~~ \text{or,}~~ 2x-4y+3z-8=0~~ \text{(ans.)}

3. Find the equation of the plane passing through the points ~(1,-1,2)~ and ~(2,-2,2)~ and which is perpendicular to the plane ~6x-2y+2z=9.

Solution.

The equation of the plane passing through the point ~(1,-1,2)~ can be written as ~~a(x-1)+b(y+1)+c(z-2)=0 \longrightarrow(1)

Since the plane (1) passes through the point ~(2,-2,2),

~a(2-1)+b(-2+1)+c(2-2)=0 \Rightarrow a-b +0 \cdot c=0\rightarrow(2)

Again, since the plane (1) is perpendicular to the plane ~6x-2y+2z=9,~ so

~6a-2b+2c=0 \longrightarrow(3)

From ~(2)~ and ~(3)~, we get by cross-multiplication,

~\frac{a}{-2+0}=\frac{b}{0-2}=\frac{c}{-2+6} \\ \text{or,}~~ \frac{a}{-2}=\frac{b}{-2}=\frac c4 \\ \text{or,}~~ \frac a1=\frac b1=\frac{c}{-2} \rightarrow(4)

Hence, using (1) and (4) we get the equation of the plane as follows :

~1 \cdot (x-1)+1 \cdot (y+1) -2 \cdot (z-2)=0 \\ \text{or,}~~ x-1+y+1-2z+4=0 \\ \text{or,}~~ x+y-2z+4=0.

Master NEET (UG) Biology with New Pattern Matching, Assertion Reason (AR), 2 Statement & Multiple Statement Questions (MSQs) 2nd Edition Paperback

4. Find the equation of the plane passing through the intersection of the planes ~~ \vec{r} \cdot (2\hat{i}+\hat{j}+3\hat{k})=7,~ \vec{r} \cdot (2\hat{i}+5\hat{j}+3\hat{k})=9~ and the point ~(2,1,3).

Solution.

Given planes are ~ \vec{r} \cdot (2\hat{i}+\hat{j}+3\hat{k})=7 \longrightarrow(1),~~ \vec{r} \cdot (2\hat{i}+5\hat{j}+3\hat{k})=9 \longrightarrow(2)

The equation of the plane passing through the planes (1) and (2), can be written as 

~[\vec{r} \cdot (2\hat{i}+\hat{j}+3\hat{k})-7 ]+\lambda[\vec{r} \cdot (2\hat{i}+5\hat{j}+3\hat{k})-9 ]=0 \\ \text{or,}~~ \vec{r} \cdot [(2+2\lambda)\hat{i}+(1+5\lambda)\hat{j}+(3+3\lambda)\hat{k}]=9\lambda+7 \longrightarrow(3)

The plane (3) passes through the point ~(2,1,3).~ The position vector of the point can be written as ~(2\hat{i}+\hat{j}+3\hat{k}).

\therefore~~(2\hat{i}+\hat{j}+3\hat{k}) \cdot [(2+2\lambda)\hat{i}+(1+5\lambda)\hat{j}+(3+3\lambda)\hat{k}]=9\lambda+7 \\ \text{or,}~~ 2(2+2\lambda)+(1+5\lambda)+3(3+3\lambda)=9\lambda+7 \\ \text{or,}~~ 4+4\lambda+1+5\lambda+9+9\lambda=9\lambda+7 \\ \text{or,}~~ 9\lambda+14=7 \Rightarrow \lambda=-\frac 79.

Now, we calculate the following values :

~2+2\lambda=2+2 \times \left(-\frac 79\right)=2-\frac{14}{9}=\frac 49,\\~~~~~1+5\lambda=1+5 \times \left(-\frac 79\right)=1-\frac{35}{9}=-\frac{26}{9},\\~~~~~3+3\lambda=3(1+\lambda)=3\left(1-\frac 79\right)=3 \times \frac 29=\frac 23,\\~~~~~ 9\lambda+7=9 \times \left(-\frac 79\right)+7=0.

Hence from (3) we get the required equation of the plane (after substituting the aforesaid values) as follows :

~\vec{r} \cdot \left[\frac 49 \cdot \hat{i}-\frac{26}{9}\hat{j}+\frac 23 \vec{k}\right]=0 \\~~~ \text{or,}~~ \vec{r} \cdot (4\hat{i}-26\hat{j}+6\hat{k})=0 \\~~~ \text{or,}~~ 2\vec{r} \cdot (2\hat{i}-13\hat{j}+3\hat{k})=0 \\~~~ \therefore~~ \vec{r} \cdot (2\hat{i}-13\hat{j}+3\hat{k})=0~~\text{(ans.)}

5. Find the equation of a plane passing through the points ~(0,0,0)~ and ~(3,-1,2)~ and parallel to the line ~ \frac{x-4}{1}=\frac{y+3}{-4}=\frac{z+1}{7}.

Solution.

The equation of the plane through the point ~(0,0,0)~ is ~ax+by+cz=0\longrightarrow(1)

Since the plane (1) passes through the point ~(3,-1,2),~~~3a-b+2c=0 \longrightarrow(2). 

Again the plane (1) is parallel to the straight line ~~~\frac{x-4}{1}=\frac{y+3}{-4}=\frac{z+1}{7}

\therefore~~a-4b+7c=0 \longrightarrow(3)

Solving (2) and (3) we get by cross-multiplication,

~\frac{a}{-7+8}=\frac{b}{2-21}=\frac{c}{-12+1} \Rightarrow \frac a1=\frac{b}{-19}=\frac{c}{-11} \rightarrow(4)

So, by using (1) and (4), we get the required equation of the plane ~~x-19y-11z=0.

6. Find the equation of the plane which is perpendicular to the plane ~5x+3y+6z+8=0~ and which contains the line of intersection of the planes ~x+2y+3z=4~ and ~2x+y-z+5=0.

Solution.

The given equations of planes are 

~5x+3y+6z+8=0\longrightarrow (1),~~x+2y+3z=4\longrightarrow (2),~~ 2x+y-z+5=0 \longrightarrow(3).

\therefore~ The equation of the plane through the planes (2) and (3) is

~(x+2y+3z-4)+\lambda(2x+y-z+5)=0 \\ \text{or,}~~ (1+2\lambda)x+(2+\lambda)y+(3-\lambda)z+(5\lambda-4)=0 \longrightarrow(4)

Since the plane (4) is perpendicular to the plane (1),

~5(1+2\lambda)+3(2+\lambda)+6(3-\lambda)=0 \\ \text{or,}~~ 5+10\lambda+6+3\lambda+18-6\lambda=0 \\ \text{or,}~~ 7\lambda+29=0 \Rightarrow \lambda=-\frac{29}{7}.

Now, we calculate the following values.

~1+2\lambda=1-2 \times \frac{29}{7}=1-\frac{58}{7}=-\frac{51}{7},~~2+\lambda=2-\frac{29}{7}=-\frac{15}{7},\\~~3-\lambda=3+\frac{29}{7}=\frac{50}{7},~~ 5\lambda-4=5 \times \left(-\frac{29}{7}\right)-4=-\frac{173}{7}.

Hence, from (4) we get the required equation of the plane (after substituting the aforesaid values) as follows :

~-\frac{51}{7}x-\frac{15}{7}y+\frac{50}{7}z-\frac{173}{7}=0 \\ \text{or,}~~ 51x+15y-50z+173=0~~\text{(ans.)}

Quickly Memorise Biology for NEET AIIMS NTA I NCERT based I Class 11 and 12 I Ktricks I Dr Kunal Tatte Paperback 

7. Find the equation of the plane through the line of intersection of the planes ~\vec{r} \cdot (2\hat{i}-3\hat{j}+4\hat{k})=1~ and ~\vec{r} \cdot (\hat{i}-\hat{j})+4=0~ and perpendicular to ~\vec{r} \cdot (2\hat{i}-\hat{j}+\hat{k})+8=0~

Solution.

The given equations of planes are ~~\vec{r} \cdot (2\hat{i}-3\hat{j}+4\hat{k})-1=0 \longrightarrow (1),~~ \vec{r} \cdot (\hat{i}-\hat{j})+4=0 \longrightarrow(2)

\therefore~ The equation of the plane through the line of intersection of  planes (1) and (2) is 

[\vec{r} \cdot (2\hat{i}-3\hat{j}+4\hat{k})-1] +\lambda[\vec{r} \cdot (\hat{i}-\hat{j})+4]=0,~~(\lambda \neq 0) \\ \text{or,}~~ \vec{r} \cdot [(2+\lambda)\hat{i}+(-3-\lambda)\hat{j}+4\hat{k}]=1-4\lambda \longrightarrow(3)

Since the plane (1) is perpendicular to the plane  ~\vec{r} \cdot (2\hat{i}-\hat{j}+\hat{k})+8=0,

[(2+\lambda)\hat{i}+(-3-\lambda)\hat{j}+4\hat{k}] \cdot (2\hat{i}-\hat{j}+\hat{k})=0 \\ \text{or,}~~ 2(2+\lambda)+(3+\lambda)+4=0 \\ \text{or,}~~ 3\lambda+11=0 \Rightarrow \lambda=-\frac{11}{3}.

Now, we calculate the following values .

~2+\lambda=2-\frac{11}{3}=-\frac 53,~~ -3-\lambda=-3+\frac{11}{3}=\frac 23,\\~~~~~~~1-4\lambda=1-4 \left(-\frac{11}{3}\right)=1+\frac{44}{3}=\frac{47}{3}.

Hence, from (3) we get the required equation of the plane (after substituting the aforesaid values) as follows :

~\vec{r} \cdot \left[-\frac 53 \hat{i}+\frac 23 \hat{j}+4\hat{k}\right]=\frac{47}{3} \\ \text{or,}~~ \vec{r} \cdot (-5\hat{i}+2\hat{j}+12 \hat{k})=47~~ \text{(ans)}

Post Views: 252

Leave a Comment