In the previous article , we have solved few VSA type questions of Plane Chapter (Ex-2B) of S N De Mathematics(Chhaya). In the following article, we are going to discuss/solve Short Answer Type Questions of S.N.Dey Mathematics-Class 12 of the chapter Plane (Ex-5B).

1. Find the equation of the plane passing through the intersection of the planes ![]() and
and ![]() and parallel to the line with direction ratios proportional to
and parallel to the line with direction ratios proportional to ![]() Find also the perpendicular distance of
Find also the perpendicular distance of ![]() from this plane. [CBSE ’05]
from this plane. [CBSE ’05]
Solution.
The given equations of the planes are ![]()
The equation of the plane passing through the intersection of planes (1) and (2) is
![]()
This plane (3) is parallel to the line with direction ratios proportional to ![]()

![]() The required equation of the plane is
The required equation of the plane is

2. Find the equation of the plane parallel to the plane ![]() and situated at a distance of
and situated at a distance of ![]() units from it.
units from it.
Solution.
The equation of any plane parallel to the plane ![]() is
is ![]()
This plane (1) is situated at a distance ![]() units from the given plane .
units from the given plane .

So, the equation of the plane is ![]() and
and ![]()
3. Find the equation of the plane passing through the intersection of the planes ![]() and
and ![]() and parallel to the line
and parallel to the line ![]()
Solution.
![]()
Equation of plane passing through the intersection of planes (1) and (2) is
![]()
The plane (3) is parallel to the straight line ![]()

Now, we calculate the following values (from (3)).
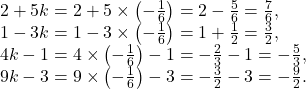
So, the required equation of the plane is given by

MTG Objective NCERT at your FINGERTIPS – Physics, Chemistry (Set of 2 Books) | NCERT NEET/JEE Trend Indicator | NCERT Notes with HD Pages (Based on NCERT Pattern – Latest & Revised Edition 2023-2024)
4. Find the distance of the point ![]() from the plane
from the plane ![]() measured along a line parallel to
measured along a line parallel to ![]()
Solution.
The equation of any straight line passing through the point ![]() and parallel to the straight line
and parallel to the straight line ![]() is
is
![]()
Any point on this straight line (1) can be written as ![]() where
where ![]() is any non-zero real number.
is any non-zero real number.
If this point lies on the plane ![]() then
then
![]()
![]() The point is
The point is
![]()
So, the required distance = The distance between ![]() and
and ![]()

5. Find the length and foot of the perpendicular from the point ![]() to the plane
to the plane ![]()
Solution.
The equation of the straight line passing through the point ![]() and perpendicular to the plane
and perpendicular to the plane ![]() is
is
![]()
The coordinates of any point on the straight line (1) can be written as ![]() where
where ![]() is any non-zero real number.
is any non-zero real number.
If this point lies on the given plane , then

Now, the distance between the points ![]() and
and ![]() is
is

The coordinates of the foot of the perpendicular is

6. Find the equation of the plane that contains the line of intersection of the planes ![]() and
and ![]() and which is perpendicular to the plane
and which is perpendicular to the plane ![]() .
.
Solution.
![]()
The equation of the plane that contains the line of intersection of planes (1) and (2) can be written as
![]()
The plane (3) is perpendicular to the plane ![]()
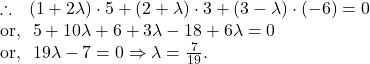
Now, we calculate the following rules (from (3)).

After substituting the aforesaid values in (3) we get the required equation of the plane as follows .
![Rendered by QuickLaTeX.com \vec{r} \cdot \left[\frac{33}{19}\hat{i}+\frac{45}{19}\hat{j}+\frac{50}{19}\hat{k}\right]-\frac{41}{19}=0 \\ \text{or,}~~ \vec{r} \cdot (33\hat{i}+45\hat{j}+50\hat{k})-41=0 \longrightarrow(4)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-2d937e8b6bcfba79be28c3e8beeefad2_l3.png)
Putting ![]() we get from (4),
we get from (4),
![]()
7. Find the distance between the point ![]() and the plane passing through
and the plane passing through ![]() and
and ![]()
Solution.
The equation of the plane passing through the points ![]() and
and ![]() is
is
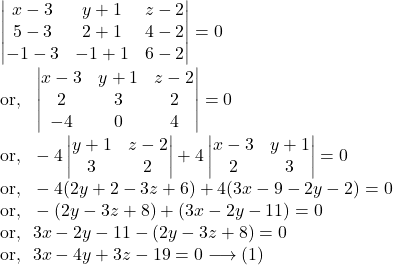
![]() Distance of the point
Distance of the point ![]() from the plane (1) is
from the plane (1) is
![]()
8. Find the equation of the plane through the points ![]() and
and ![]() and find the distance of this plane from the point
and find the distance of this plane from the point ![]() \
\
Hints : Follow Question No. 7
High Yield NEET MCQs – 12th Physics – NEETprep.com (2000+ High Yield NCERT Based Questions with Video/Text Solutions) Paperback
9. Find the equation of the plane through the points ![]() and parallel to the line
and parallel to the line ![]() Convert to vector form.
Convert to vector form.
Solution.
The equation of the plane passing through the point ![]() is
is
![]()
The plane (1) is passing through the point ![]()

Since the plane is parallel to the straight line ![]()
![]()
Eliminating ![]() from (1), (2), (3) we get,
from (1), (2), (3) we get,

![]() The vector equation of (4) is
The vector equation of (4) is
![]() where
where ![]()
10. Show that the lines ![]() and
and ![]() are coplanar.
are coplanar.
Solution.

The straight line (1) passes through the point ![]() and is parallel to
and is parallel to ![]()

Again, the straight line (2) passes through the point ![]() and is parallel to
and is parallel to ![]()
Clearly, given two straight lines are coplanar whenever ![]() and
and ![]() are coplanar.
are coplanar.
![Rendered by QuickLaTeX.com \therefore~~ \begin{vmatrix} (b-c)-(a-d) & b-a &(b+c)-(a+d) \\ \alpha-\delta& \alpha &\alpha+\delta \\ \beta-\gamma &\beta &\beta+\gamma \\ \end{vmatrix}\\= \begin{vmatrix} d-c & b-a &c-d \\ -\delta& \alpha &\delta \\ -\gamma& \beta &\gamma \\ \end{vmatrix},~~[C_1' \rightarrow C_1-C_2,~~C_3' \rightarrow C_3-C_2]\\= \begin{vmatrix} 0& b-a & c-d \\ 0& \alpha & \delta \\ 0& \beta & \gamma \\ \end{vmatrix}=0 \\ \therefore~~[\vec{AB}~~ \vec{p}~~\vec{q}]=0.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-5e5961b217f6e07a849707f0c4cb8e16_l3.png)
![]() are coplanar and hence the result follows.
are coplanar and hence the result follows.

