In the previous article , we discussed Very Short Answer Type Questions. In this article, we will discuss 10 Short Answer type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Short Answer Type Questions of Circle, S N Dey Mathematics, Class 11
1. Find the equation of the circle whose centre is ![]() and which passes through the centre of the circle
and which passes through the centre of the circle ![]()
Solution.
The equation of the circle with centre ![]() and radius
and radius ![]() can be written as :
can be written as :
![]()
By the given question, ![]() Putting these values of
Putting these values of ![]() in
in ![]() we get from
we get from ![]()
![]()
Now, comparing the given the circle ![]() with the general equation of circle
with the general equation of circle ![]() we get ,
we get ,
![]()
Hence, the centre of the given circle is : ![]()
Now, since the circle as represented by ![]() passes through
passes through ![]() we get,
we get,

Hence, from ![]() we get the required equation of circle which is :
we get the required equation of circle which is :
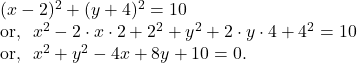
2. Find the equation of the circle concentric with the circle ![]() and passing through the point
and passing through the point ![]()
Solution.
Now, comparing the given the circle ![]() with the general equation of circle
with the general equation of circle ![]() we get ,
we get ,
![]()
So, the centre of the circle ![]() , is :
, is : ![]()
Also, the equation of the circle with the centre ![]() is given by
is given by
![]()
Since the circle represented by ![]() passes through the point
passes through the point ![]() we get,
we get,
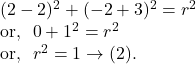
Hence, from ![]() we get the required the equation of the circle which is
we get the required the equation of the circle which is
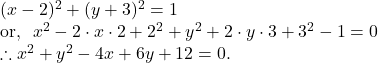
Hence, the equation of the circle concentric with the circle ![]() and passing through the point
and passing through the point ![]() is
is ![]()
3. Find the equation of the circle concentric with the circle ![]() and passing through the centre of the circle
and passing through the centre of the circle ![]()
Solution.
Comparing the given the circle ![]() with the general equation of circle
with the general equation of circle ![]() we get ,
we get ,
![]()
Since we need to find the equation of the circle concentric with the circle ![]() i.e. with the centre
i.e. with the centre ![]() , the equation of the circle with radius
, the equation of the circle with radius ![]() can be written as
can be written as ![]()
Now, we have to find the centre of the circle ![]()
Comparing the given the circle ![]() with the general equation of circle
with the general equation of circle ![]() we get ,
we get ,
![]()
So, the centre of the circle : ![]()
Now, the circle represented by ![]() passes through the point
passes through the point ![]() so
so
![]()
Finally, from ![]() we get the equation of the circle which is
we get the equation of the circle which is

Hence, the required equation of the circle is ![]()
4. Find the equation of the straight line which passes through the centre of the circle ![]() and is perpendicular to the straight line
and is perpendicular to the straight line ![]()
Solution.
The equation of the straight line which is perpendicular to the straight line ![]() can be written as :
can be written as : ![]() being an arbitrary constant.
being an arbitrary constant.
Now, we need to find the centre of the circle ![]()
Comparing the given the circle ![]() with the general equation of circle
with the general equation of circle ![]() we get ,
we get ,
![]()
Hence, the centre of the circle ![]() is given by
is given by ![]()
Now, since the straight line ![]() passes through the point
passes through the point ![]() we have
we have
![]()
Finally putting the value of ![]() in
in ![]() , we get the required equation of the straight line which is
, we get the required equation of the straight line which is ![]()
5. Find the equation of each of the circles passing through the points
![]()
Solution.
We know that the general form of the equation of a circle is
![]()
Since the circle in ![]() passes through the points
passes through the points ![]() we get
we get

Now, putting the value of ![]() in
in ![]() we get,
we get,
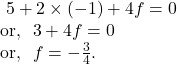
Hence, by putting the values of ![]() in
in ![]() we get the required equation of circle which is
we get the required equation of circle which is

6.Show that the points ![]() and
and ![]() are concylic ; find the equation of the circle on which the points lie and the co-ordinates of the centre of the circle.
are concylic ; find the equation of the circle on which the points lie and the co-ordinates of the centre of the circle.
Solution.
The general equation of circle ![]()
Since the points ![]() and
and ![]() are concylic, we get from
are concylic, we get from ![]()
![]()

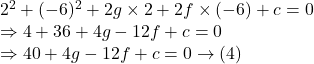
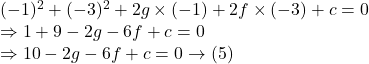
Subtracting ![]() from
from ![]() we get
we get

Subtracting ![]() from
from ![]() we get
we get

From ![]() , we get
, we get
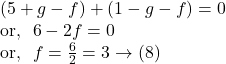
From ![]() we get,
we get,
![]()
Putting the value of ![]() in
in ![]() we get,
we get,
![]()
Hence, the equation of the required circle is
![]()
Comparing ![]() with the general equation of circle
with the general equation of circle ![]() we get ,
we get ,
![]()
Hence, the co-ordinates of the centre of the circle is ![]()
7. Prove that the centres of the circles ![]() and
and ![]() lie on a line; find the equation of the line on which they lie.
lie on a line; find the equation of the line on which they lie.
Solution.
We know that the general form of the equation of a circle is ![]()
The centre of the circle represented by ![]() is
is ![]()
Now, comparing ![]() with
with ![]() we get,
we get,
![]()
So, the centre of the circle represented by ![]() is
is ![]()
Similarly, the centre of the circle ![]() is
is ![]() and the centre of the circle
and the centre of the circle ![]() is
is ![]()
Now, the equation of the line passing through ![]() is :
is :
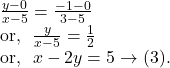
Now, the putting ![]() in
in ![]() we get,
we get, ![]()
Hence, the point ![]() satisfies the equation
satisfies the equation ![]()
So, the centres of three circles lie on the line ![]()
8. Show that the centres of the following circles lie on a line and their radii are in A.P. : ![]()
Solution.
The equation of the first circle can be written as ![]() so that we can say the centre of the first circle is
so that we can say the centre of the first circle is ![]() and radius is
and radius is ![]() unit.
unit.
The equation of the second circle is ![]() so that the the centre of the second circle is :
so that the the centre of the second circle is :
![]()
Also, the radius is :
![]()
The equation of the third circle is ![]() so that the the centre of the third circle is :
so that the the centre of the third circle is :
![]()
Also, the radius is :
![]()
Clearly, the radii of three circles are ![]() respectively and so
respectively and so ![]() and so the radii are in A.P.
and so the radii are in A.P.
Again, the slope of the straight line joining the points ![]() and
and ![]() is :
is : ![]()
Also, the slope of the straight line joining the points ![]() and
and ![]() is :
is : ![]()
Hence, from ![]() and
and ![]() we can conclude that the centres of the following circles lie on a line.
we can conclude that the centres of the following circles lie on a line.
9. Find the equation of the circle which passes through the origin and cuts off intercepts ![]() unit and
unit and ![]() unit from
unit from ![]() and
and ![]() -axes respectively. Find the equation of that diameter of the circle which passes through the origin.
-axes respectively. Find the equation of that diameter of the circle which passes through the origin.
Solution.
Suppose that the circle which passes through the origin , cuts off intercepts ![]() unit and
unit and ![]() unit from
unit from ![]() and
and ![]() -axes at the point
-axes at the point ![]() and
and ![]() respectively. Then,
respectively. Then, ![]()
The circle passes through the origin and ![]()

![]() is the diameter of the circle, the equation of the circle having diameter
is the diameter of the circle, the equation of the circle having diameter ![]() with
with ![]() can be written as
can be written as
![]()
Now , we need to find the equation of the diameter of this circle which passes through the ![]() .
.
The centre of the circle is ![]()
Now, the diameter of this circle passes through ![]()
So, the equation of the straight line which passes through ![]() is given by :
is given by :
![]()
10. Find the equation of the circle circumscribing the triangle formed by the straight line ![]() with the axes of co-ordinates. What is the diameter of the circle ?
with the axes of co-ordinates. What is the diameter of the circle ?
Solution.
Let the given straight line intercepts the axes of co-ordinates at the points ![]() and
and ![]() respectively.
respectively.
Now, ![]()
From ![]() we notice that the straight line cuts off
we notice that the straight line cuts off ![]() units from the
units from the ![]() axis and
axis and ![]() units from
units from ![]() axis.
axis.
![]()

Now, ![]() Clearly,
Clearly, ![]() is a right angled triangle and
is a right angled triangle and ![]() is the mid point of
is the mid point of ![]() which is a diameter of circumscribed circle with extremities
which is a diameter of circumscribed circle with extremities ![]()
Now, the equation of the circle having diameter ![]() with
with ![]() can be written as
can be written as
![]()
Also, diameter ![]()