In the previous article , we discussed Very Short Answer Type Questions. In this article, we will discuss 10 more Short Answer type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Short Answer Type Questions of Circle, S N Dey Mathematics, Class 11
11. The extremities of a diameter of a circle are the points ![]() and
and ![]() ; Find the equation of the circle. Also find the equation of that diameter of this circle which passes through the origin.
; Find the equation of the circle. Also find the equation of that diameter of this circle which passes through the origin.
Solution.
The equation of any circle having the extremities ![]() and
and ![]() of a diameter is given by
of a diameter is given by
![]()
Now, we need to find the equation of that diameter of this circle which passes through the origin.
The centre of the circle is ![]()
Hence equation of the diameter that passes through ![]() and
and ![]() is given by :
is given by :
![]()
12. Find the equation of the circle through the points ![]() and
and ![]() and having its centre on the line
and having its centre on the line ![]()
Solution.
Let ![]() be the centre of the circle.
be the centre of the circle.
Since ![]() lies on the line
lies on the line ![]()
![]()
Again, since the circle passes through the points ![]() and
and ![]() , the distance of
, the distance of ![]() from the points
from the points ![]() and
and ![]() , will be same.
, will be same.
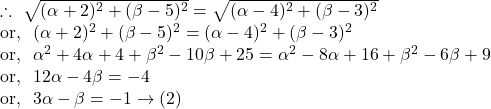
Now, solving ![]() and
and ![]() we get,
we get, ![]()
So, the centre of the circle is ![]() and the radius of the circle is
and the radius of the circle is
![]()
Hence, the equation of the circle is
![]()
13. A circle has its centre on the straight line ![]() and cuts off the
and cuts off the ![]() axis at the two points whose abscissae
axis at the two points whose abscissae ![]() and
and ![]() find the equation of the circle and its radius.
find the equation of the circle and its radius.
Solution.
The general form of the equation of the circle can be written as
![]() where
where ![]() is the centre of the circle and the radius
is the centre of the circle and the radius ![]()
According to the problem, the circle passes through the points ![]() and
and ![]()
So, by ![]() we get
we get
![]()
Similarly, by ![]() we get
we get
![]()
Subtracting ![]() from
from ![]() we get,
we get,
![]()
Since the circle has its centre on the straight line ![]() , so
, so![]()
Putting the value of ![]() in
in ![]() we get
we get
![]()
Now, putting the value of ![]() in
in ![]() we get
we get
![]()
By ![]() we get the radius
we get the radius ![]()
By ![]() we get the equation of the circle as
we get the equation of the circle as
![]()
14. The equation of a diameter of a circle is ![]() and it passes through the points
and it passes through the points ![]() and
and ![]() Find the equation of the circle , the co-ordinates of its centre and length of its radius.
Find the equation of the circle , the co-ordinates of its centre and length of its radius.
Solution.
Let ![]() be the centre of the circle so that
be the centre of the circle so that ![]() as the diameter of the circle passes through the centre of the circle.
as the diameter of the circle passes through the centre of the circle.
Again, the circle passes through the points ![]() and
and ![]() so the centre
so the centre ![]() is equidistant from the points
is equidistant from the points ![]() and
and ![]()

Solving ![]() we get,
we get, ![]()
So, the centre of the circle is ![]() and radius of the circle is
and radius of the circle is ![]()
![]() the equation of the circle
the equation of the circle
![]()
15. A circle passes through through the points ![]() and its radius is
and its radius is ![]() unit ; find the equation of the circle.
unit ; find the equation of the circle.
Solution.
Let the centre of the circle be ![]()
![]() the equation of the circle can be written as
the equation of the circle can be written as
![]() which passes through the points
which passes through the points ![]() and
and ![]()
![]()
![]()
Now, subtracting ![]() from
from ![]() we get,
we get,

By using ![]() we get,
we get,
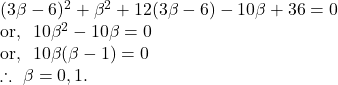
![]()
So, the required equation of the circle is
![]() and
and ![]()
or, ![]()
![]() and
and ![]() are two diameters to the circle which passes through the point
are two diameters to the circle which passes through the point ![]() . Find its equation. Also find the radius of the circle.
. Find its equation. Also find the radius of the circle.
Solution.
Clearly, the centre of the circle will be the intersection of two given diameters.
![]() and
and ![]() are two given diameters.
are two given diameters.
Solving ![]() we get,
we get, ![]()
So, the centre of the circle is : ![]() Also, it is given that the circle passes through the point
Also, it is given that the circle passes through the point ![]() .
.
Hence, the radius ![]()
Finally, the equation of the circle is

17. A circle passes through the points ![]() and its centre lies on the
and its centre lies on the ![]() axis. Find the equation of the circle.
axis. Find the equation of the circle.
Solution.
Let the centre of the circle ![]() because the centre lies on the
because the centre lies on the ![]() axis. Since the circle passes through the points
axis. Since the circle passes through the points ![]() , the points are equidistant from the centre of the circle.
, the points are equidistant from the centre of the circle.
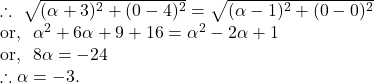
![]() the centre of the circle
the centre of the circle ![]()
![]() the radius of the circle
the radius of the circle ![]()
![]() the equation of the circle is
the equation of the circle is
![]()
18. Find the equation of the circle which has its centre on the line ![]() and which passes through the points
and which passes through the points ![]() and
and ![]()
Solution.
Let the centre of the circle be ![]() as its centre lie on the line
as its centre lie on the line ![]()
Since the circle passes through the points ![]() , the points are equidistant from the centre of the circle.
, the points are equidistant from the centre of the circle.

![]() the centre of the circle
the centre of the circle ![]() and radius
and radius ![]()
![]() the equation of the circle is
the equation of the circle is

19. Find the equation to the circle which touches the ![]() axis at the origin and passes through the point
axis at the origin and passes through the point ![]()
Solution.
Since the circle which touches the ![]() axis at the origin, from the following figure we notice that the centre
axis at the origin, from the following figure we notice that the centre ![]() of the circle lies on the
of the circle lies on the ![]() axis.
axis.
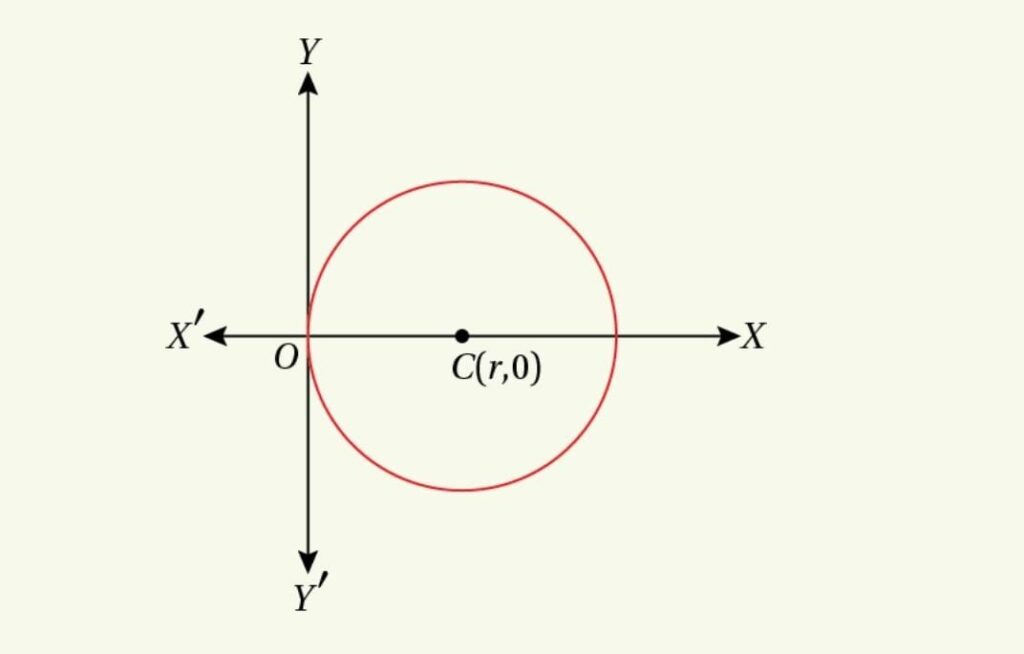
Let the radius of the circle ![]() and the co-ordinate of the centre of the circle
and the co-ordinate of the centre of the circle ![]() Now, since the circle passes through the point
Now, since the circle passes through the point ![]() the radius of the circle is the distance between
the radius of the circle is the distance between ![]() and
and ![]()

Now, the equation of the circle with centre ![]() and radius
and radius ![]() is
is
![Rendered by QuickLaTeX.com (x-r)^2+y^2=r^2 \\ \text{or,}~~ x^2-2rx+r^2+y^2=r^2 \\ \text{or,}~~x^2+y^2-2rx=0 \\ \text{or,}~~ x^2+y^2-\frac{2x(\alpha^2+\beta^2)}{2\alpha}=0 ~~[\text{By (1)}] \\ \text{or,}~~\alpha(x^2+y^2)=x(\alpha^2+\beta^2).](https://examhoop.com/wp-content/ql-cache/quicklatex.com-bf4955b368f5fcd6f7c60cb0271159ff_l3.png)
20. A circle touches the ![]() axis at
axis at ![]() and its radius is twice the radius of the circle
and its radius is twice the radius of the circle ![]() find the equation of the circle and the length of its chord intercepted on the
find the equation of the circle and the length of its chord intercepted on the ![]() axis.
axis.
Solution.
We can rearrange the given circle as
![]()
So, the radius of the circle as represented by ![]() is
is ![]() unit. Our circle of concern will have a radius of
unit. Our circle of concern will have a radius of ![]() units. Now, suppose that the centre of circle of concern is
units. Now, suppose that the centre of circle of concern is ![]() so that the equation of circle can be written as
so that the equation of circle can be written as
![]()
Now, the circle in ![]() passes through
passes through ![]() so that
so that
![]()
![]() the equation of the circle
the equation of the circle

Comparing ![]() with the general form of the equation of circle
with the general form of the equation of circle ![]() we get,
we get, ![]()
So, the length of the chord cut on ![]() axis
axis
![]()