In the previous article , we discussed few Short Answer Type Questions. In this article, we will discuss 9 more Short Answer type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Short Answer Type Questions of Circle, S N Dey Mathematics, Class 11
21. A circle touches ![]() axis at
axis at ![]() and whose centre lies on the line
and whose centre lies on the line ![]() find the equation of the circle.
find the equation of the circle.
Solution.
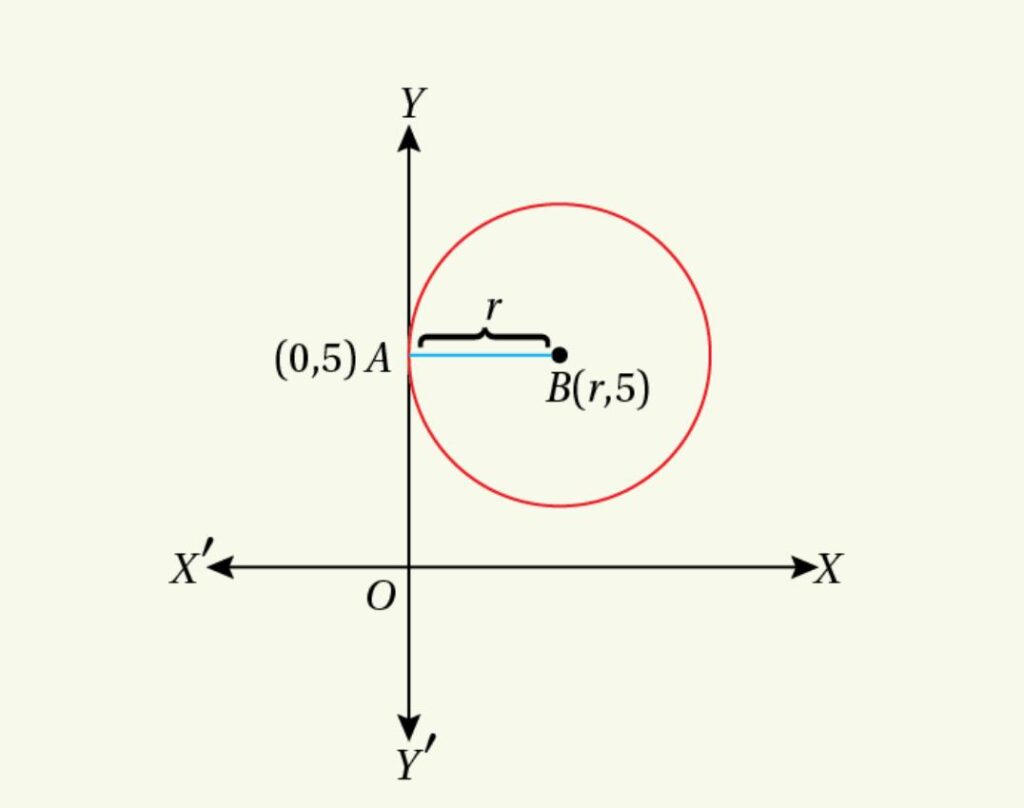
Let the radius of the circle be ![]() unit. The circle touches the
unit. The circle touches the ![]() axis at the point
axis at the point ![]() Now, since
Now, since ![]() where
where ![]() and the centre of the circle is
and the centre of the circle is ![]()
Since the centre of the circle lies on ![]()
so ![]()
![]() the centre of the circle is
the centre of the circle is ![]() and the radius is
and the radius is ![]() unit.
unit.
![]() the equation of the circle is
the equation of the circle is

22. Find the equation of a circle which passes through the point ![]() and touches both the co-ordinate axes. How many of such circles are possible ?
and touches both the co-ordinate axes. How many of such circles are possible ?
Solution.
Let the radius of the circle be ![]() unit and the circle touches
unit and the circle touches ![]() axis and
axis and ![]() axis at
axis at ![]() and
and ![]() respectively.
respectively.
![]()
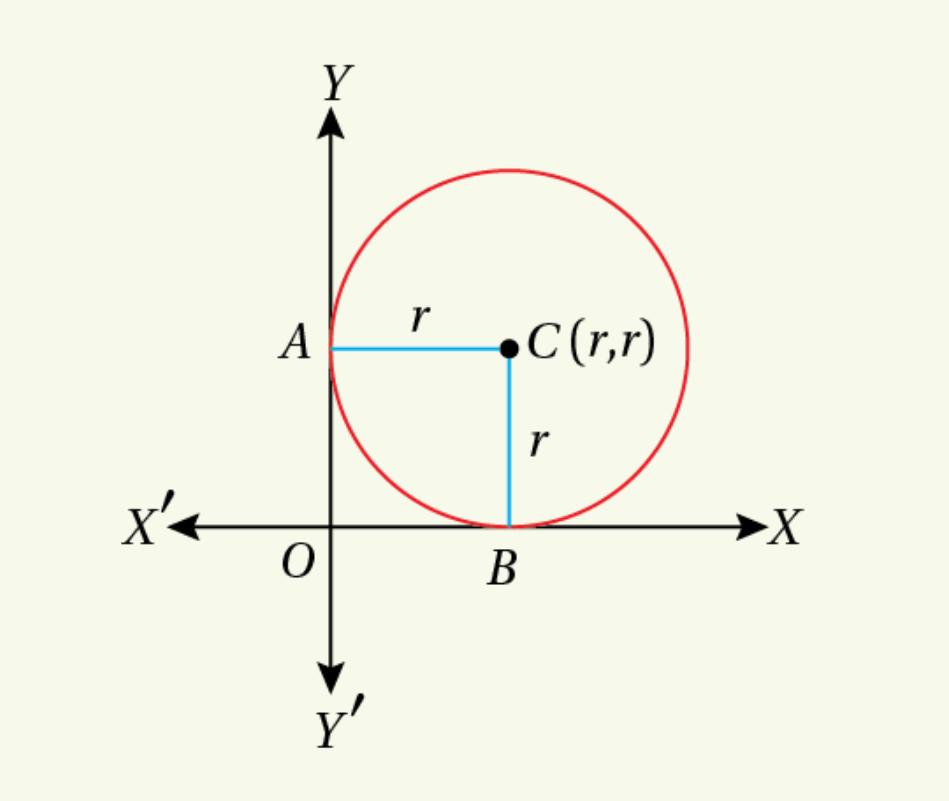
![]() the co-ordinates of
the co-ordinates of ![]() is
is ![]()
So, the equation of the circle can be written as
![]() which passes through
which passes through ![]()

Finally, by ![]() and
and ![]() , the equation of circle can be written as
, the equation of circle can be written as
![]() or,
or, ![]()
So, from the aforementioned discussions we can conclude that two such circles are possible.
23. Two circles of radii ![]() and
and ![]() units respectively pass through
units respectively pass through ![]() and touch both the
and touch both the ![]() and
and ![]() axes. Find the equations of the two circles . Also find the other common point of intersection.
axes. Find the equations of the two circles . Also find the other common point of intersection.
Solution.
Since the circles passes through the point ![]() which lies in the first quadrant and since the given circles touch both the
which lies in the first quadrant and since the given circles touch both the ![]() and
and ![]() axes, so the circles lie in the first quadrant.
axes, so the circles lie in the first quadrant.
Suppose that the circle with radius ![]() unit touches
unit touches ![]() axis at the point
axis at the point ![]() and touches
and touches ![]() axis at
axis at ![]() .
.
![]()
Now from the following figure, we can notice that the co-ordinates of ![]() is
is ![]()

So, the equation of the circle

Similarly, we can determine that the equation of the circle with radius ![]() unit is given by
unit is given by

Now, we need to determine the other common point intersection.
Subtracting ![]() from
from ![]() we get,
we get,

From ![]() and
and ![]() we get that for
we get that for ![]() the corresponding values of
the corresponding values of ![]()
So, common points of intersection of two circles are given by ![]() and
and ![]()
Hence, the other common point of intersection is ![]()
24. Prove that the ![]() lies on the circle
lies on the circle ![]() Find the co-ordinates of the other extremity of the diameter through
Find the co-ordinates of the other extremity of the diameter through ![]()
Solution.
Putting ![]() in the equation of the circle
in the equation of the circle ![]() we get
we get ![]() and so the point
and so the point ![]() lies on the given circle.
lies on the given circle.
Comparing ![]() with the general form of the circle
with the general form of the circle ![]() we get,
we get,
![]()
So, the centre of the given circle ![]()
Let the other extremity of the circle be ![]()
Since the the point ![]() lies on the circle, so the centre of the circle will be the midpoint of the straight line joining the points
lies on the circle, so the centre of the circle will be the midpoint of the straight line joining the points ![]() and
and ![]() which is
which is ![]()
![]()
Hence, the co-ordinates of the other extremity of the diameter through ![]() is
is ![]()
25. Show that for all values of ![]() , the circle
, the circle ![]() passes the point
passes the point ![]() If
If ![]() varies , find the locus of the centre of the above circle.
varies , find the locus of the centre of the above circle.
Solution.
Since the given circle ![]() passes the point
passes the point ![]() putting
putting ![]() in
in ![]() we get
we get

So, ![]() satisfy the given equation of the circle. So, the circle passes through the point
satisfy the given equation of the circle. So, the circle passes through the point ![]() for any values of
for any values of ![]()
Comparing ![]() with the general form of the circle
with the general form of the circle ![]() we get,
we get,
![]()
So, the centre of the circle ![]()
If ![]() is the centre of the circle, then
is the centre of the circle, then
![]() and
and ![]()
From ![]() we get
we get ![]()
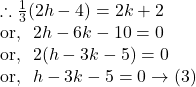
Finally, by ![]() we can conclude that the locus of the centre of the circle is
we can conclude that the locus of the centre of the circle is ![]()
26. Find the co-ordinates of the points equidistant from the axes and lying on the circle ![]()
Solution.
The given equation of circle can be rewritten as :

Let the co-ordinates of the points equidistant from the axes be ![]()
Since the point ![]() lies on the given circle,
lies on the given circle,
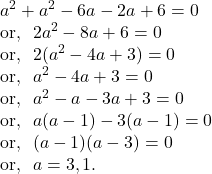
The co-ordinates of the points equidistant from the axes are ![]()
Again, since the point ![]() lies on the given circle,
lies on the given circle,
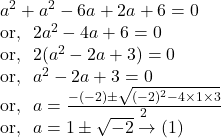
So, by ![]() we get the imaginary values of
we get the imaginary values of ![]() and so we can discard those values.
and so we can discard those values.
27. Find the equation to the common chord of the two circles ![]() and
and ![]() and also find its length.
and also find its length.
Solution.
The equation to the common chord of the two circles ![]() and
and ![]() is
is
![]()
From ![]() we get,
we get, ![]()
By ![]() and
and ![]() we get by replacing the value of
we get by replacing the value of ![]()
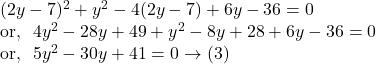
Let the roots of the equation in ![]() be
be ![]()
![]() and
and ![]()
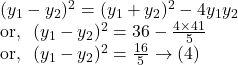
Let the chord intersects the circles at the points ![]() and
and ![]() .
.
![]() and
and ![]()
So, the length of the chord is

28. Find the equation of the common chord of the two circles ![]() and
and ![]() Show that this chord is perpendicular to the line joining the centres of two circles.
Show that this chord is perpendicular to the line joining the centres of two circles.
Solution.
The equation of two given circles are ![]() and
and ![]()
Now, subtracting ![]() from
from ![]() we get
we get
![]()
So, equation in ![]() represents the equation of the common chord of two circles.
represents the equation of the common chord of two circles.
The co-ordinates of centre of circle ![]() is
is ![]() and the co-ordinates of centre of circle
and the co-ordinates of centre of circle ![]() is
is ![]()
Now, the slope of the straight line joining two centres of the circles is ![]()
Again , the slope of the straight line ![]() is
is ![]()
So, ![]()
Finally, by ![]() we can conclude that this chord is perpendicular to the line joining the centres of two circles.
we can conclude that this chord is perpendicular to the line joining the centres of two circles.
29. Find the equation of the circle which passes through the origin and the points of intersection of the circles ![]() and
and ![]()
Solution.
The equation of the circle through the points of intersection of the circles ![]() and
and ![]() is
is
![]()
Since the circle ![]() passes through the origin, putting
passes through the origin, putting ![]() in
in ![]() we get,
we get,
![]()
![]() the equation of the circle is
the equation of the circle is
