Circle | Part-6 | S N Dey Examhoop

In the previous article , we discussed few Short Answer Type Questions. In this article, we will discuss few more Short Answer type Questions from Chhaya Mathematics , Class 11 (S N De book ).

Short Answer Type Questions related to Circle , S N Dey Mathematics | Class 11 | WBCHSE

30. A point moves in such a manner that the sum of the squares of its distance from the origin and the point $~(2,-3)~$ is always $~19.~$ Show that the locus of the moving point is a circle. Find the equation to the locus.

Solution.

Suppose that at any instant the co-ordinates of the moving point is $~(h, k).$

So, according to the problem,

$(\sqrt{(h-0)^2+(k-0)^2})^2+(\sqrt{(h-2)^2+(k+3)^2})^2=19 \\ \text{or,}~~ h^2+k^2+(h-2)^2+(k+3)^2=19 \\ \text{or,}~~ h^2+k^2+h^2-4h+4+k^2+6k+9=19 \\ \text{or,}~~ 2h^2+2k^2-4h+6k-6=0 \\ \text{or,}~~ h^2+k^2-2h+3k-3=0 \rightarrow(1)$

Hence, by $(1)~$ we get the locus of the point $~(h,k)~$ which is $~x^2+y^2-2x+3y-3=0~$ which represents the equation of a circle.

31. $~A(3,0)~$ and $~B(-3,0)~$ are two given points and $~P~$ is a moving point ; if $~\overline{AP}=2\overline{BP}~$ for all positions of $~P~$ , show that the locus of $~P~$ is a circle . Find the radius of the circle.

Solution.

Suppose that at any instant the the co-ordinates of the moving point $~P~$ is $~(h, k).$

$\text{By question,}~~ \overline{AP}=2\overline{BP} \\ \text{or,}~~ \sqrt{(h-3)^2+(k-0)^2}=2\sqrt{(h+3)^2+(k-0)^2} \\ \text{or,}~~(h-3)^2+k^2=4(h+3)^2+4k^2 \\ \text{or,}~~h^2-6h+9+k^2=4h^2+24h+36+4k^2 \\ \text{or,}~~ 3h^2+3k^2+30h+27=0 \\ \text{or,}~~h^2+k^2+10h+9=0 \rightarrow(1)$

Hence, by $(1)~$ we get the locus of the point $~(h,k)~$ which is $~x^2+y^2+10x+9=0~$ which represents the equation of a circle.

Comparing the circle with $~x^2+y^2+2gx+2fy+c=0~$ we get, $~g=5,~f=0,~c=9.$

The radius of the circle is

$\sqrt{g^2+f^2-c}=\sqrt{5^2+0^2-9}=\sqrt{16}=4~\text{unit}.$

32. Show that the locus of the point of intersection of the lines $~x\cos\alpha+y\sin\alpha=a~$ and $~x\sin\alpha-y\cos\alpha=a,~$ when $~\alpha~$ varies, is a straight line.

Solution.

Suppose that at any instant the point of intersection of two straight lines is $~(h,k).$

$\therefore~ h\cos\alpha+k\sin\alpha=a \rightarrow(1),~~ h\sin\alpha-k\cos\alpha=a\rightarrow(2)$

From $~(1)~$ and $~(2),~$ we get

$(h\cos\alpha+k\sin\alpha)^2+(h\sin\alpha-k\cos\alpha)^2=2a^2 \\ \text{or,}~~(\cos^2\alpha+\sin^2\alpha)h^2+(\sin^2\alpha+\cos^2\alpha)k^2\\~~+2hk\cos\alpha\sin\alpha-2hk\sin\alpha\cos\alpha=2a^2 \\ \text{or,}~~ h^2+k^2=2a^2\rightarrow(3)$

So, by $~(3),~$ we get the locus of the point of intersection of the lines is

$~x^2+y^2=2a^2~$ which represents the equation of a circle.

33. Whatever be the values of $~\theta~$ , prove that the locus of the point of intersection of the straight lines $~y=x\tan\theta~$ and $~x\sin^3\theta+y\cos^3\theta=a\sin\theta \cos\theta~$ is a circle. Find the equation of the circle.

Solution.

Suppose that at any instant the point of intersection of two straight lines is $~(h,k).$

$\therefore~ k=h\tan\theta \rightarrow(1)~$ and

$h\sin^3\theta+k\cos^3\theta=a\sin\theta\cos\theta \\ \text{or,}~~ h\sin^3\theta+h\tan\theta\cos^3\theta=a\sin\theta\cos\theta~ ~[\text{By (1)}] \\ \text{or,}~~h\sin^3\theta+h\sin\theta\cos^2\theta=a\sin\theta\cos\theta \\ \text{or,}~~ h\sin\theta(\sin^2\theta+\cos^2\theta)=a\sin\theta\cos\theta \\ \text{or,}~~h\sin\theta=a\sin\theta\cos\theta \\ \text{or,}~~ h=a\cos\theta \rightarrow(2)$

Putting the value of $~h~$ in $~(1),~$ we get

$~k=a\cos\theta \tan\theta \Rightarrow k=a\sin\theta \rightarrow(3)$

Hence, by $~(4),~$ we get that the locus of the point of intersection of the straight lines is $~x^2+y^2=a^2~$ which represents the equation of a circle.

34. Show that, $~x=\frac 12(3+5\cos\theta),~y=\frac 12(-4+5\sin\theta)~$ represent a circle passing through the origin. Find the co-ordinates of the centre and length of radius of the circle.

Solution.

$x=\frac 12(3+5\cos\theta) \Rightarrow x-\frac 32=\frac 52 \cos\theta\rightarrow(1),\\~~y=\frac 12(-4+5\sin\theta) \Rightarrow y+2=\frac 52\sin\theta\rightarrow(2)$

Squaring both sides of $~(1)~$ and $~(2)~$ and adding , we get

$(x-3/2)^2+(y+2)^2=(5/2)^2(\cos^2\theta+\sin^2\theta) \\ \text{or,}~~(x-3/2)^2+(y+2)^2=(5/2)^2\rightarrow(3)$

Clearly, $~(3)~$ represents the equation of the circle with centre $~(3/2,-2)~$ and radius $~5/2~$ unit.

35. Prove that the square of the distance between the two points $~(x_1,y_1)~$ and $~(x_2,y_2)~$ of the circle $~x^2+y^2=a^2~$ is $~2(a^2-x_1x_2-y_1y_2).$

Solution.

Since the points $~(x_1,y_1)~$ and $~(x_2,y_2)~$ lies on the given circle, so

$x_1^2+y_1^2=a^2 \rightarrow(1),~~x_2^2+y_2^2=a^2\rightarrow(2)$

The square of the distance between the two points $~(x_1,y_1)~$ and $~(x_2,y_2)~$ of the circle is

$(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2})^2\\=(x_1-x_2)^2+(y_1-y_2)^2\=x_1^2-2x_1x_2+x_2^2+y_1^2-2y_1y_2+y_2^2\\=(x_1+x_2)^2+(y_1+y_2)^2-2x_1x_2-2y_1y_2\\=a^2+a^2-2x_1x_2-2y_1y_2 ~~[\text{By (1),(2)}]\\=2(a^2-x_1x_2-y_1y_2)~~\text{(proved)}$

36. The equations of two diameters of a circle are $~x-2y+1=0~$ and $~x+y-2=0~$ and the length of the chord intercepted on the straight line $~3x+4y+8=0~$ by the circle is $~6~$ units. Find the equation of the circle.

Solution.

The centre of the circle is the intersection of $~x-2y+1=0 \rightarrow(1)~$ and $~x+y-2=0\rightarrow(2).$

Solving $~(1)~$ and $~(2)~$ , we get $~x=1,~y=1.$

So, the centre of the circle is $~C(1,1).$

From the figure, we notice that $~~ CA \perp BD.$

$~CA=$ the distance of the given straight line from the point $~C$

$=\frac{3 \times 1+4 \times 1+8}{\sqrt{3^2+4^2}}=3.$

From the figure, we notice that the the length of the chord $~(BD)~$ intercepted on the straight line $~3x+4y+8=0~$ by the circle is $~6~$ so that $~BA=\frac 12 BD=\frac 12 \times 6=3.$

$BC^2=BA^2+CA^2 \\ \text{or,}~ BC^2=3^2+3^2 \\ \text{or,}~ BC=\sqrt{9+9}=3\sqrt{2}.$

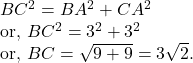
So, the radius of the circle is $~3\sqrt{2}~$ unit and centre is $~(1,1).$

$\therefore~$ the equation of the circle

$(x-1)^2+(y-1)^2=(3\sqrt{2})^2 \\ \text{or,}~~ x^2-2x+1+y^2-2y+1=18 \\ \text{or,}~~ x^2+y^2-2x-2y-16=0.$

37. Find the equation of the circle circumscribing the rectangle whose sides are given by $~x-3y=4,~3x+y=22,~x-3y=14~$ and $~3x+y=62.$

Solution.

From the figure, we notice that the point $~A~$ is the intersection of the straight lines
$~ x-3y=14~\rightarrow(1)$ and $~3x+y=22~\rightarrow(2).$

Now, solving $~(1)~$ and $~(2)~$ we get, the co-ordinates of $~A \equiv(8,-2).$

Again, from the figure, we notice that the point $~C~$ is the intersection of the straight lines $~ x-3y=4~\rightarrow(3)$ and $~3x+y=62~\rightarrow(4).$