In the previous article, we have discussed the solutions of VSA type questions of Integration By Parts Chapter of S N Dey mathematics Class 12. In this chapter, we will discuss the problems of Short Answer Type Questions.

Integration By Parts | Short Ans Type Questions | S N Dey
Integrate :
![]()
Solution.
![Rendered by QuickLaTeX.com ~I\\=\displaystyle\int{x^2\sin x}~dx\\=x^2\int{\sin x}-\int{\left[\frac{d}{dx}(x^2)\int{\sin x}~dx\right]}~dx\\=-x^2\cos x-\int{2x(-\cos x)}~dx\\=-x^2\cos x+2\int{x\cos x~dx}\\=-x^2\cos x+2I_1 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-73dc52f2b0903f5c792f1e6a0d107805_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{x\cos x~dx}\\=x\int{\cos x}dx-\int{[\frac{d}{dx}(x)\int{\cos x~dx}]}~dx\\=x\sin x-\int{\sin x~dx}\\=x\sin x+\cos x\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-4b440c8c08acafe7696db87b3ea85710_l3.png)
Hence, by ![]() we get,
we get,
![]()
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{(x+1)^2\log x}~dx\\=\log x \int{(x+1)^2}~dx-\int{\left[\frac{d}{dx}(\log x) \int{(x+1)^2~dx}\right]}~dx\\=\log x \int{z^2~dz}-\int{\left[\frac 1x~\int{z^2~dz}\right]}~dz~~[~\text{let}~z=x+1 \Rightarrow~dz=dx]\\=\log x~ \cdot \frac{z^3}{3}-\int{\frac 1x \times \frac{z^3}{3}~dz}\\=\frac 13(x+1)^3~\log x-\frac 13\int{\frac{(x+1)^3}{x}}~dx\\=\frac 13(x+1)^3~\log x-\frac 13 \int{\frac{x^3+3x^2+3x+1}{x}}~dx\\=\frac 13(x+1)^3~\log x-\frac 13 \int{(x^2+3x+3+\frac 1x)}~dx\\=\frac 13(x+1)^3~\log x-\frac 13\left[\frac{x^3}{3}+3 \cdot \frac{x^2}{2}+3x+\log |x|\right]+c\\=\frac 13\left[(x+1)^3~\log x-\frac{x^3}{3}-\frac{3x^2}{2}-3x-\log|x|\right]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-d10cc51ae7c45cf132a9a6e01eb862e4_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{x\tan^{-1}x}~dx\\=\tan^{-1}x\int{x~dx}-\int{\left[\frac{d}{dx}(\tan^{-1}x)\int{x~dx}\right]}~dx\\=\frac{x^2}{2}\tan^{-1}x- \int{\frac{1}{1+x^2} \times \frac{x^2}{2}~dx}\\=\frac{x^2}{2}\tan^{-1}x-\frac 12 \int{\frac{1+x^2-1}{1+x^2}}~dx\\=\frac{x^2}{2}\tan^{-1}x-\frac 12 \int{\left(1-\frac{1}{1+x^2}\right)}~dx\\=\frac{x^2}{2}\tan^{-1}x-\frac 12\int{dx}+\frac 12 \int{\frac{dx}{1+x^2}}\\=\frac{x^2}{2}\tan^{-1}x-\frac x2+\frac 12 \tan^{-1}x\\=\frac 12\left[(x^2+1)\tan^{-1}x-x\right]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-31c9a9ee65121bb35588c60e5fc7dd26_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com ~\displaystyle\int{\frac{\log(1-x)}{x^2}}~dx\\=\log(1-x)\int{\frac{dx}{x^2}}-\int{\left[\frac{d}{dx}{\log(1-x)}\int{\frac{dx}{x^2}}\right]}~dx\\=\log(1-x)\left[\frac{x^{-2+1}}{-2+1}\right]-\int{-\frac{1}{1-x} \times {\frac{x^{-2+1}}{-2+1}}}~dx\\=-\frac 1x\log(1-x)-\int{\frac{dx}{x(1-x)}}\\=-\frac 1x\log(1-x)-\int{\left[\frac{1-x+x}{x(1-x)}\right]}~dx\\=-\frac 1x\log(1-x)-\int{\left[\frac{1}{x}+\frac{1}{1-x}\right]}~dx\\=-\frac 1x\log(1-x)-\int{\frac{dx}{x}}-\int{\frac{dx}{1-x}}\\=-\frac 1x\log(1-x)-\log x+\log(1-x)+c\\=(1-\frac 1x)\log(1-x)-\log x+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-806203b7faea3bdb340d1b29596cb999_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{x^3e^{ax}}~dx\\=x^3\int{e^{ax}~dx}-\int{\left[\frac{d}{dx}(x^3)\int{e^{ax}~dx}\right]}~dx\\=x^3 \cdot \frac{e^{ax}}{a}-\int{3x^2 \cdot \frac{e^{ax}}{a}}~dx\\=x^3 \cdot \frac{e^{ax}}{a}-\frac 3aI_1, ~\text{where}~I_1=\int{x^2e^{ax}~dx}\ \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-b35f0c2073b9d9390af060cb612b9afb_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{x^2e^{ax}~dx}\\=x^2\int{e^{ax}}~dx-\int{\left[\frac{d}{dx}(x^2)\int{e^{ax}~dx}\right]}~dx\\=x^2 \cdot \frac{e^{ax}}{a}-\int{2x \cdot \frac{e^{ax}}{a}}~dx\\=x^2 \cdot \frac{e^{ax}}{a}-\frac 2a I_2 \rightarrow(2) \\~~I_2\\=\int{xe^{ax}}~dx\\=x\int{e^{ax}~dx} -\int{\left[\frac{d}{dx}(x) \int{e^{ax}~dx}\right]}~dx\\=x \cdot\frac{e^{ax}}{a}-\int{1 \cdot \frac{e^{ax}}{a}}~dx\\=x \cdot\frac{e^{ax}}{a}-\frac 1a \int{e^{ax}}~dx\\=x \cdot\frac{e^{ax}}{a}-\frac 1a \cdot \frac 1ae^{ax}\\=x \cdot\frac{e^{ax}}{a}-\frac{e^{ax}}{a^2}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-515bf703ef2990c0cef3f00d6c149bf2_l3.png)
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{x^3e^{ax}}~dx\\=x^3 \cdot \frac{e^{ax}}{a}-\frac 3a\left[x^2 \cdot \frac{e^{ax}}{a}-\frac 2a \left(x \cdot\frac{e^{ax}}{a}-\frac{e^{ax}}{a^2}\right)\right]\\=e^{ax}\left(\frac{x^3}{a}-\frac{3x^2}{a^2}+\frac{6x}{a^3}-\frac{6}{a^4}\right)+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-e486eaa5318a1e554c6da99a610b8d4e_l3.png)
![]()
Solution.

![Rendered by QuickLaTeX.com ~I_1\\=\displaystyle\int{\cos^{-1}x}~dx\\=\cos^{-1}x \int{dx}-\int{\left[\frac{d}{dx}(\cos^{-1}x)\int{dx}\right]}\\=x\cos^{-1}x-\displaystyle\int{\left(-\frac{1}{\sqrt{1-x^2}}\right) \times x}~dx\\=x\cos^{-1}x+\int{\frac{x}{\sqrt{1-x^2}}}~dx \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-5e1a691bda06b375ff1df30002cf1bae_l3.png)
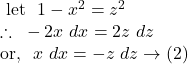
Hence, by ![]() we get,
we get,
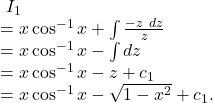
![Rendered by QuickLaTeX.com ~I_2\\=\displaystyle\int{\log x}\\=\log x\int{dx}-\int{\left[\frac{d}{dx}(\log x) \int{dx}\right]}~dx\\=x\log x-\int{\frac 1x \times x~dx}\\=x\log x-\int{dx}\\=x\log x-x+c_2.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-923c4af8fd7440df73d73d6cc432fcde_l3.png)
![Rendered by QuickLaTeX.com \therefore~\displaystyle\int{(\cos^{-1}x+\log x)}~dx\\=(x\cos^{-1}x-\sqrt{1-x^2}+c_1)+(x\log x-x+c_2)\\=x\cos^{-1}x-\sqrt{1-x^2}+x(\log x-1)+c~~[~c=c_1+c_2].](https://examhoop.com/wp-content/ql-cache/quicklatex.com-81874b52a5930bf3d94efaddd0808150_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{(\log\sqrt{x})^2}~dx\\=(\log\sqrt{x})^2\int{dx}-\int{\left[\frac{d}{dx}(\log\sqrt{x})^2\int{dx}\right]}~dx\\=x(\log\sqrt{x})^2-\int{2\log{\sqrt{x}} \cdot \frac{1}{\sqrt{x}} \cdot \frac{1}{2\sqrt{x}} \cdot x~dx}\\=x(\frac 12\log x)^2-\int{\log{\sqrt{x}}~dx}\\=\frac x4(\log x)^2-\frac 12 \int{\log x~dx}\\=\frac x4(\log x)^2-\frac 12I_1 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-cd862ecfb63eac9c09cf651d4aad5136_l3.png)
![Rendered by QuickLaTeX.com ~I_1\\=\log x\displaystyle\int{dx}-\int{\left[\frac{d}{dx}(\log x) \int{dx}\right]}~dx\\=x\log x-\int{\frac 1x \times x~dx}\\=x\log x-\int{dx}\\=x\log x-x+c_1\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-fcf9bd3eaaab276f2451bdac166d8a5d_l3.png)
Hence, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com ~\displaystyle\int{(\log\sqrt{x})^2}~dx\\=\frac x4(\log x)^2-\frac 12(x \log x-x+c_1)\\=\frac x4[(\log x)^2-2\log x+2]+c.~~\left[~c=-\frac{c_1}{2}\right]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-fe9288caf9121051d96594eea355ff19_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\log(x^2-5x+6)}~dx\\=\int{\log[(x-3)(x-2)]~dx}\\=\int{\log(x-3)~dx+\int{\log(x-2)~dx}}\\=I_1+I_2,~~\text{(say)}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-d6ffe2bd96efd1859eb72d4f8bee7684_l3.png)
![Rendered by QuickLaTeX.com ~I_1\\=\displaystyle\int{\log(x-3)}~dx\\=\int{\log z}~dz~~[\text{where}~x-3=z~]\\=\log z\int{dz}-\int{\left[\frac{d}{dz}(\log z) \int{dz}\right]}~dz\\=z\log z-\int{\frac 1z \times z}~dz\=z\log z-\int{dz}\\=z\log z-z+c_1\\=(x-3)\log(x-3)-(x-3)+c_1](https://examhoop.com/wp-content/ql-cache/quicklatex.com-fb677622971f6489c82c735635ed732c_l3.png)
![Rendered by QuickLaTeX.com ~I_2\\=\displaystyle\int{\log(x-2)}~dx\\=\int{\log z}~dz~~~[\text{where}~x-2=z~] \\=\log z\int{dz}-\int{\left[\frac{d}{dz}(\log z) \int{dz}\right]}~dz\\=z\log z-\int{\frac 1z \times z}~dz\\=z\log z-\int{dz}\=z\log z-z+c_1\\=(x-2)\log(x-2)-(x-2)+c_2](https://examhoop.com/wp-content/ql-cache/quicklatex.com-82283ac18e5e17e391b23ddf226a0c5d_l3.png)
![Rendered by QuickLaTeX.com ~\therefore~\displaystyle\int{\log(x^2-5x+6)}~dx\\=(x-3)\log(x-3)-(x-3)+c_1+(x-2)\log(x-2)-(x-2)+c_2\\=(x-3)\log(x-3)+(x-2)\log(x-2)-2x+(c_1+c_2+5)\\=(x-3)\log(x-3)+(x-2)\log(x-2)-2x+c.~~[~c=c_1+c_2+5~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-63cd43d75af21536c358faea6a180616_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com ~\displaystyle\int{x^3(\log x)^2}~dx\\=(\log x)^2 \times \int{x^3~dx}-\int{\left[\frac{d}{dx}(\log x)^2 \int{x^3~dx}\right]}~dx\\=(\log x)^2 \times \frac{x^4}{4}-\int{2\log x \cdot \frac 1x \cdot \frac{x^4}{4}}~dx\\=\frac{x^4}{4}(\log x)^2-\frac 12\int{\log x\cdot x^3~dx}\\=\frac{x^4}{4}(\log x)^2-\frac 12I_1\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-3ed75bc713bb2e379bdf3f4f653cdaef_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{\log x \cdot x^3}~dx\\=\log x \int{x^3~dx}-\int{\left[\frac{d}{dx}(\log x) \int{x^3}~dx\right]}~dx\\=\log x \cdot \frac{x^4}{4}-\int{\frac 1x \cdot \frac{x^4}{4}}~dx\\=\frac{x^4}{4}(\log x)-\frac 14\int{x^3}~dx\\=\frac{x^4}{4}(\log x)-\frac 14 \times \frac{x^4}{4}\\=\frac{x^4}{4}(\log x)-\frac{x^4}{16}+c_1\rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-e25f0a039af97281fc42ae3ef0b5defd_l3.png)
From ![]() we get,
we get,
![Rendered by QuickLaTeX.com ~\displaystyle\int{x^3(\log x)^2}~dx\\=\frac{x^4}{4}(\log x)^2-\frac 12\left[\frac{x^4}{4}(\log x)-\frac{x^4}{16}+c_1\right]\\=\frac{x^4}{4}\left[(\log x)^2-\frac 12(\log x)+\frac 18\right]+c.~~[~c=-c_1/2]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-6dba6948d13cdcc8a7bbecb9549531d2_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{\log(x+\sqrt{x^2-a^2})}~dx\\=\log(x+\sqrt{x^2-a^2})\int{dx}-\int{\left[\frac{d}{dx}(\log(x+\sqrt{x^2-a^2}))\int{dx}\right]}~dx\\=x\log(x+\sqrt{x^2-a^2})-\int{\frac{1}{x+\sqrt{x^2-a^2}}\left(1+\frac{2x}{2\sqrt{x^2-a^2}}\right)\cdot x~dx}\\=x\log(x+\sqrt{x^2-a^2})-\int{\frac{1}{x+\sqrt{x^2-a^2}}\left(1+\frac{x}{\sqrt{x^2-a^2}}\right)\cdot x~dx}\\=x\log(x+\sqrt{x^2-a^2})-\int{\frac{1}{x+\sqrt{x^2-a^2}}\left(\frac{\sqrt{x^2-a^2}+x}{\sqrt{x^2-a^2}}\right)\cdot x~dx}\\=x\log(x+\sqrt{x^2-a^2})-\int{\frac{x}{\sqrt{x^2-a^2}}}~dx\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-63666e1caeddf7a2fb4a36233f725f6f_l3.png)
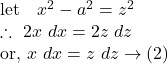
From ![]() we get,
we get,
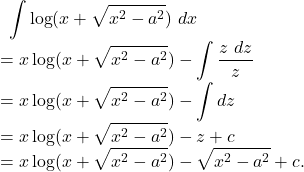
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{x\log(x+\sqrt{x^2+a^2})}~dx\\=\log(x+\sqrt{x^2+a^2}) \int{x~dx}-\int{\left[\frac{d}{dx}(\log(x+\sqrt{x^2+a^2}))\int{x~dx}\right]}~dx\\=\frac{x^2}{2}\log(x+\sqrt{x^2+a^2})-\int{\frac{1}{(x+\sqrt{x^2+a^2})}\cdot\left(1+\frac{2x}{2\sqrt{x^2+a^2}}\right) \cdot\frac{x^2}{2}}~dx\\=\frac{x^2}{2} \log(x+\sqrt{x^2+a^2})-\frac 12 \int{\frac{1}{(x+\sqrt{x^2+a^2})} \cdot \left(1+\frac{x}{\sqrt{x^2+a^2}}\right)\cdot x^2~dx}\\=\frac{x^2}{2}\log(x+\sqrt{x^2+a^2})-\frac 12\int{\frac{1}{(x+\sqrt{x^2+a^2})} \cdot \frac{\sqrt{x^2+a^2}+x}{\sqrt{x^2+a^2}} \cdot x^2~dx}\\=\frac{x^2}{2} \log(x+\sqrt{x^2+a^2})-\frac 12\int{\frac{x^2}{\sqrt{x^2+a^2}}~dx}\\=\frac{x^2}{2}\log(x+\sqrt{x^2+a^2})-\frac 12I_1\rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c28e0e98e2ec52f9ce42dcbba05b12a7_l3.png)
![]()
![]()
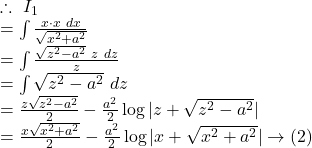
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{x\log(x+\sqrt{x^2+a^2})}~dx\\=\frac{x^2}{2}\log(x+\sqrt{x^2+a^2})-\frac 12 \left[\frac{x\sqrt{x^2+a^2}}{2}-\frac{a^2}{2}\log|x+\sqrt{x^2+a^2}|\right]+c](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c7db967c0451edcb346c85e7e7b3ba7e_l3.png)