In the previous article, we have discussed the solutions of VSA type questions of Integration By Parts Chapter of S N Dey mathematics Class 12. In this chapter, we will discuss the problems of Short Answer Type Questions.

Short Answer Type Questions of Integration By Parts :
![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{x^2\cos2x}~dx\\=x^2\int{\cos2x}~dx-\int{\left[\frac{d}{dx}(x^2)\int{\cos2x}~dx\right]}~dx\\=x^2 \cdot (\frac 12 \sin2x)-\int{2x \cdot (\frac 12 \sin2x)}~dx\\=\frac{x^2}{2}\sin2x-\int{x\sin2x~dx}\\=\frac{x^2}{2}\sin2x-I_2](https://examhoop.com/wp-content/ql-cache/quicklatex.com-e6319758b0695424bebdfc2af129d103_l3.png)
![Rendered by QuickLaTeX.com I_2\\=\displaystyle\int{x\sin2x}~dx\\=x\int{\sin2x}~dx-\int{\left[\frac{d}{dx}(x)\int{\sin2x}~dx\right]}~dx\\=x \cdot (-\frac 12 \cos2x)-\int{(-\frac 12\cos2x)}~dx\\=-\frac x2 \cos2x+\frac 12 \cdot \frac{\sin2x}{2}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-ad6b63051331e13695a49d44b210b557_l3.png)

![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{x\sec^2(x/2)}~dx\\=x\int{\sec^2(x/2)}~dx+\int{\left[\frac{d}{dx}(x)\int{\sec^2(x/2)}~dx\right]}~dx\\=x \cdot 2\tan(x/2)-\int{1 \cdot (2\tan(x/2))}~dx\\=2x\tan(x/2)-2\int{\tan(x/2)}~dx](https://examhoop.com/wp-content/ql-cache/quicklatex.com-eab248477a8db1f73de1676871890f77_l3.png)

![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{x^210^{2x}}~dx\\=x^2\int{10^{2x}}~dx- \int{\left[\frac{d}{dx}(x^2)\int{10^{2x}}~dx\right]}~dx\\=x^2 \cdot \frac{10^{2x}}{2\log 10}-\int{2x \cdot \frac{10^{2x}}{2\log 10}}~dx\\=x^2 \cdot \frac{10^{2x}}{2\log 10}-\frac{1}{\log 10} \int{x \cdot10^{2x}}~dx\\=x^2 \cdot \frac{10^{2x}}{2\log 10}-\frac{1}{\log 10}I_1.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-ea83d1fc61093cc55daedea6275d95d2_l3.png)
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{x \cdot10^{2x}}~dx\\=x\int{10^{2x}}~dx-\int{\left[\frac{d}{dx}(x)\int{10^{2x}}~dx\right]}~dx\\=x \cdot \frac{10^{2x}}{2\log 10}-\frac{1}{2\log 10}\int{10^{2x}}~dx\\=x \cdot \frac{10^{2x}}{2\log 10}-\frac{1}{2\log 10} \cdot \frac{10^{2x}}{2\log 10}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-8172ec8422c28f050b4544f66e95fbf8_l3.png)
![Rendered by QuickLaTeX.com \therefore~~ \displaystyle\int{x^210^{2x}}~dx\\=x^2 \cdot \frac{10^{2x}}{2\log 10}-\frac{1}{\log 10}\left(x \cdot \frac{10^{2x}}{2\log 10}-\frac{1}{2\log 10} \cdot \frac{10^{2x}}{2\log 10}\right)\\= \frac{10^{2x}}{2\log 10} \left[x^2-\frac{x}{\log 10}+\frac{1}{2(\log 10)^2}\right]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-50510d12ee218c06c77be6f616374b97_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{x^2\sin^{-1}(3x)}~dx\\=\sin^{-1}(3x)\int{x^2}~dx-\int{\left[\frac{d}{dx}(\sin^{-1}(3x))\int{x^2}~dx\right]}~dx\\=\frac{x^3}{3}\sin^{-1}(3x)-\int{\frac{3}{\sqrt{1-(3x)^2}}\cdot \frac{x^3}{3}}~dx\\=\frac{x^3}{3}\sin^{-1}(3x)-\int{\frac{x^3}{\sqrt{1-9x^2}}}~dx\\=\frac{x^3}{3}\sin^{-1}(3x)-\int{\frac{x^2 \cdot x}{\sqrt{1-9x^2}}}~dx\\=\frac{x^3}{3}\sin^{-1}(3x)-I_1](https://examhoop.com/wp-content/ql-cache/quicklatex.com-f0d0d060f841a02792f8e96c4ea85b95_l3.png)

![Rendered by QuickLaTeX.com \therefore~I_1\\=\displaystyle\int{\frac{x^2 \cdot x}{\sqrt{1-9x^2}}}~dx\\=-\frac 19\int{\frac{1-z^2}{9} \cdot \frac 1z \cdot z}~dz\\=-\frac{1}{81}\left[z-\frac{z^3}{3}\right]\\=-\frac{1}{81}\left[\sqrt{1-9x^2}-\frac{(1-9x^2)\sqrt{1-9x^2}}{3}\right]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-9a58499d479f5a0fba141bc9a3a12994_l3.png)
![Rendered by QuickLaTeX.com ~\therefore~\displaystyle\int{x^2\sin^{-1}(3x)}~dx\\=\frac{x^3}{3}\sin^{-1}(3x)+\frac{1}{81}\left[\sqrt{1-9x^2}-\frac{(1-9x^2)\sqrt{1-9x^2}}{3}\right]\\=\frac{x^3}{3}\sin^{-1}(3x)+\frac{1}{81}\sqrt{1-9x^2}\left[1-\frac{1-9x^2}{3}\right]\\=\frac{x^3}{3}\sin^{-1}(3x)+\frac{1}{81}\sqrt{1-9x^2} \left[\frac{3-1+9x^2}{3}\right]\\=\frac{x^3}{3}\sin^{-1}(3x)+\frac{1}{243}(2+9x^2)\sqrt{1-9x^2}+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-27af71a1d32145f2076b0bf75cb12fa0_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{(\sin^{-1}x)^2}~dx\\=(\sin^{-1}x)^2\int{dx}-\int{\left[\frac{d}{dx}(\sin^{-1}x)^2\int{dx}~\right]}~dx\\=x(\sin^{-1}x)^2-\int{2\sin^{-1}x \cdot \frac{1}{\sqrt{1-x^2}} \cdot x}~dx\\=x(\sin^{-1}x)^2-2I_1.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-106a5d56efdd2decc5f7612705bd54ca_l3.png)
![]()
![]()
From ![]() we get,
we get,
![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{z\sin z}~dz\\=z\int{\sin z}~dz-\int{\left[\frac{d}{dx}(z)\int{\sin z}~dz\right]}~dz\\=z(-\cos z)+\int{1 \cdot \cos z}~dz\\=-z\cos z+\sin z\=-z\sqrt{1-\sin^2z}+\sin z\=-(\sin^{-1}x))\sqrt{1-x^2}+x](https://examhoop.com/wp-content/ql-cache/quicklatex.com-e8922ee86735cd73f77d5e6e9e5d70a1_l3.png)
![Rendered by QuickLaTeX.com \therefore~ \displaystyle\int{(\sin^{-1}x)^2}~dx \\=x(\sin^{-1}x)^2-2\left[-(\sin^{-1}x))\sqrt{1-x^2}+x\right]+c\\=x(\sin^{-1}x)^2+2\sqrt{1-x^2}~\sin^{-1}x-2x+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-5efe92f1562c8a23c8dd896207bff9dc_l3.png)
![]()
Solution.


![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{\sin^{-1}x}~dx\\=\sin^{-1}x\int{dx}-\int{\left[\frac{d}{dx}(\sin^{-1}x)\int{~dx}\right]}~dx\\=x\sin^{-1}x-\int{\frac{1}{\sqrt{1-x^2}} \cdot x}~dx\\=x\sin^{-1}x-I_2.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-948d47109ee7629717eb168fb6773abb_l3.png)
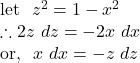
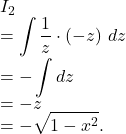

![]()
Solution.

![Rendered by QuickLaTeX.com I_1\\=\displaystyle\int{\tan^{-1}x}~dx\\=\tan^{-1}x\int{dx}-\int{\left[\frac{d}{dx}(\tan^{-1}x)\int{~dx}\right]}~dx\\=x\tan^{-1}x-\int{\frac{1}{1+x^2} \cdot x~dx}\\=x\tan^{-1}x-\frac 12\int{\frac{2x}{1+x^2}}~dx\\=x\tan^{-1}x-\frac 12\int{\frac{d(1+x^2)}{1+x^2}}\\=x\tan^{-1}x-\frac 12\log|1+x^2|](https://examhoop.com/wp-content/ql-cache/quicklatex.com-721abddc4bd359f04f5abe8a2341a30f_l3.png)

![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{\frac{\cos^{-1}x}{x^3}}~dx\\=\cos^{-1}x\int{\frac{1}{x^2}}~dx-\int{\left[\frac{d}{dx}(\cos^{-1}x)\int{\frac{1}{x^2}}~dx\right]}~dx\\=(\cos^{-1}x) \times \frac{x^{-3+1}}{-3+1}-\int{\frac{-1}{\sqrt{1-x^2}} \times \frac{x^{-3+1}}{-3+1}}~dx\\=-\frac{\cos^{-1}x}{2x^2}-\frac 12\int{\frac{1}{x^2\sqrt{1-x^2}}}~dx\\=-\frac{\cos^{-1}x}{2x^2}-\frac 12I_1 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-d8c59a80ea07f88df657b47812c65501_l3.png)
![]()
Then, by ![]() we get,
we get,
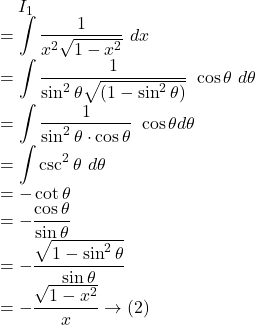
Hence, by ![]() we get,
we get,
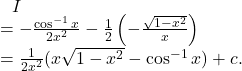
![]()
Solution.
![]()

![Rendered by QuickLaTeX.com I_1\\=\int{\theta\sin2\theta}~d\theta\\=\theta\int{\sin2\theta}~d\theta-\int{\left[\frac{d}{d\theta}(\theta)\int{\sin2\theta}~d\theta\right]}~d\theta\\=\theta \cdot \left(-\frac{\cos2\theta}{2}\right)-\int{\left(-\frac{\cos2\theta}{2}\right) }\theta\\=-\frac 12(\theta\cos2\theta)+\frac 12\int{\cos2\theta}~d\theta\\=-\frac 12(\theta\cos2\theta)+\frac 12 \cdot \frac{\sin2\theta}{2}](https://examhoop.com/wp-content/ql-cache/quicklatex.com-32c88b31199cb0f7a1046953bc561084_l3.png)
![Rendered by QuickLaTeX.com I\\=-2\left[-\frac 12(\theta\cos2\theta)+\frac 12 \cdot \frac{\sin2\theta}{2}\right]\\=\theta\cos2\theta-\frac 12\sin2\theta+c\\=\theta\cos2\theta-\frac 12\sqrt{1-\cos^22\theta}+c\\=\frac 12\cos^{-1}x \cdot x-\frac{\sqrt{1-x^2}}{2}+c\\=\frac 12(x\cos^{-1}x-\sqrt{1-x^2}) +c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-270c74e8b5358ee35e59406eb52476c3_l3.png)