In this article, we will discuss the solutions of Long Answer Type Questions (31-42) in the chapter Integration By Parts (Ex-7) as given in the Chhaya Publication Book (Class 12) of aforementioned chapter of S N De book.

Integration By Parts | S N Dey | Ex-7 | Long Answer Type Solution
![]()
Solution.

![]()
Hence, from ![]() we get,
we get,
![Rendered by QuickLaTeX.com I\\=\sqrt{3}\displaystyle\int{\sqrt{z^2-\left(\frac 43\right)^2}}~dz\\=\sqrt{3}\left[\frac z2 \sqrt{z^2-\left(\frac 43\right)^2}-\frac{\left(\frac 43\right)^2}{2}\log \left|z+\sqrt{z^2-\left(\frac 43\right)^2}\right|\right] +c\\=\sqrt{3} \left[\frac{x+\frac 53}{2} \cdot \sqrt{\left(x+\frac 53\right)^2-\left(\frac 43\right)^2}-\frac{16}{9 \times 2}\log \left|\left(x+\frac 53\right)+\sqrt{x^2+\frac{10x}{3}+1}\right|\right]+c\\=\sqrt{3} \left[\frac 16(3x+5) \cdot \frac{\sqrt{3x^2+10x+3}}{\sqrt{3}}-\frac 89\log \left|\left(x+\frac 53\right)+\sqrt{x^2+\frac{10x}{3}+1}\right| \right]+c\\=\frac{3x+5}{6} \sqrt{3x^2+10x+3}-\frac{8\sqrt{3}}{9}\log \left|\left(x+\frac 53\right)+\sqrt{x^2+\frac{10x}{3}+1}\right|+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-31c0110427707970374acc8ceb696753_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com ~ \displaystyle\int{\frac{x^2+1}{\sqrt{1-x^2}}}~dx\\=\int{\frac{2-(1-x^2)}{\sqrt{1-x^2}}}~dx\\=2\int{\frac{1}{\sqrt{1-x^2}}}~dx -\int{\frac{1-x^2}{\sqrt{1-x^2}}}~dx\\=2\sin^{-1}x-\left[\frac x2 \sqrt{1-x^2}+\frac 12 \sin^{-1}x\right]+c\\=\frac 32\sin^{-1}x-\frac x2\sqrt{1-x^2}+c\\=\frac 12(3\sin^{-1}x-x\sqrt{1-x^2})+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-cd6bbf93dbe993cbc5a2c5ef592fafeb_l3.png)
![]()
Solution.
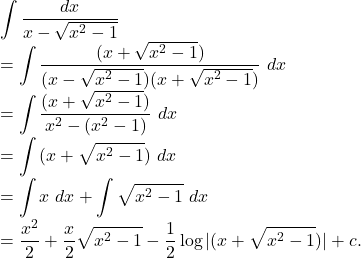
![]()
Solution.
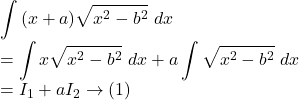
![]()
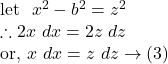
Hence, by ![]() we get,
we get,


Finally, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{(x+a)\sqrt{x^2-b^2}}~dx\\=\frac 13(x^2-b^2)^{\frac 32}+c_1 +a\left(\frac{x\sqrt{x^2-b^2}}{2}-\frac{b^2}{2}\log|x+\sqrt{x^2-b^2}|+c_2\right)\\=\frac 13(x^2-b^2)^{\frac 32}+\frac 12 ax\sqrt{x^2-b^2}-\frac{ab^2}{2}\log|x+\sqrt{x^2-b^2}|+c~~[*]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-fc98671962d4a4b4ba01f9e42a328086_l3.png)
Note[*] : ![]()
![]()
Solution.

![]()
By ![]() we get,
we get,
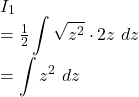
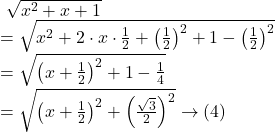
![Rendered by QuickLaTeX.com I_2\\=\displaystyle\int{\sqrt{\left(x+\frac 12\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2}}~dx \\= \int{\sqrt{z^2+\left(\frac{\sqrt{3}}{2}\right)^2}}~dz~\left[~z=x+\frac 12~\right] \\= \frac z2 \sqrt{z^2+\left(\frac{\sqrt{3}}{2}\right)^2}+\frac{\left(\frac{\sqrt{3}}{2}\right)^2}{2} \log\left|z+\sqrt{z^2+\left(\frac{\sqrt{3}}{2}\right)^2}\right|+c_2 \\=\frac{x+\frac 12}{2} \sqrt{\left(x+\frac 12\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2} + \frac 38 \log \left|x+\frac 12+\sqrt{\left(x+\frac 12\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2}\right|+c_2\rightarrow(5)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-dbe8fbf59d6d0faf7fe49b2beb0aeb59_l3.png)
Finally, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com \displaystyle\int{(x-1)\sqrt{x^2+x+1}}~dx\\= \frac 13(x^2+x+1)^{\frac 32}+c_1-\frac 32 \left[\frac{x+\frac 12}{2} \sqrt{\left(x+\frac 12\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2} + \frac 38 \log \left|x+\frac 12+\sqrt{\left(x+\frac 12\right)^2+ \left(\frac{\sqrt{3}}{2}\right)^2}\right|+c_2\right]\\= \frac 13(x^2+x+1)^{\frac 32}-\frac{3(2x+1)}{8} \sqrt{x^2+x+1} -\frac{9}{16}\log \left|x+\frac 12+\sqrt{\left(x+\frac 12\right)^2+ \left(\frac{\sqrt{3}}{2}\right)^2}\right|+c~~[*]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-9c1fad83af7be698064e17b1b6ea38c0_l3.png)
Note [*] : ![]()
Read More :
| Sl No. | Download Link | |
| 1 | Chhaya Math Solution of Integration By Parts | Click here |
| 2 | Chhaya Math Solution of Product of Two Vectors | Click here |
| 3 | Chhaya Math Solution of Linear Differential Equation | Click here |
![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{xe^x \sin x}~dx \\=x\int{e^x}~dx- \int{\left[\frac{d}{dx}(x) \int{e^x\sin x}~dx\right]}~dx\\=x \cdot \frac{e^x(\sin x-\cos x)}{2}-\int{1 \cdot \frac{e^x (\sin x-\cos x)}{2}}~dx\\=\frac{xe^x(\sin x-\cos x)}{2}-\frac 12 \int{e^x(\sin x-\cos x)}~dx \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-8bde7aef7c022027990e5298048a5d19_l3.png)
![Rendered by QuickLaTeX.com \text{Now,}~~\displaystyle\int{e^x(\sin x-\cos x)}~dx\\=-\int{e^x(\cos x-\sin x)}~dx\\=-\int{e^x[f(x)+f'(x)]}~dx~~[*]\\=-e^xf(x)+c\\=-e^x \cos x+c \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-dd65336b16a3062451358babe4b281b0_l3.png)
Note [*] : ![]()
Hence, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com ~I=\frac{xe^x(\sin x-\cos x)}{2}+\frac 12e^x\cos x+c\\~~\\ ~\text{or,}~I=\frac{e^x}{2}[x(\sin x-\cos x)+\cos x]+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-d6387a25f2dadd81e2ed3f23cc0b1352_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{[\sin(\log x)+\cos(\log x)]}~dx \\=\int{\sin(\log x)}~dx+\int{\cos(\log x)}~dx\\=\sin(\log x)\int{dx}-\int{\left[\frac{d}{dx}(\sin(\log x)) \int{dx}\right]}~dx+\int{\cos(\log x)}~dx\\=x\sin(\log x)-\int{\cos(\log x) \cdot \frac 1x \cdot x~dx}+\int{\cos(\log x)}~dx\\= x\sin(\log x)-\int{\cos(\log x)}~dx+\int{\cos(\log x)}~dx+c\\=x\sin(\log x)+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-65070ccf98e24c73d6953264244135fe_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com \displaystyle\int{(e^{\log x}+\sin x) \cos x}~dx \\=\int{(x+\sin x) \cos x}~dx\\=\int{x\cos x}~dx+\int{\sin x\cos x}~dx\\=x\int{\cos x}~dx-\int{\left[\frac{d}{dx}(x) \int{\cos x}~dx\right]}~dx+\frac 12\int{\sin2x}~dx\\=x\sin x-\int{\sin x}~dx+\frac 12 \left(-\frac{\cos2x}{2}\right)+c\\=x\sin x+\cos x-\frac 14\cos 2x+c.](https://examhoop.com/wp-content/ql-cache/quicklatex.com-5a9ae3be343d20235b14bd97f16ea912_l3.png)
![]()
Solution.
![Rendered by QuickLaTeX.com I\\=\displaystyle\int{\sin(\log x)}~dx\\=\sin(\log x)\int{dx}-\int{\left[\frac{d}{dx}(\sin(\log x)) \int{1 \cdot}~dx\right]}~dx\\=x\sin(\log x)-\int{\cos(\log x) \cdot \frac 1x \cdot x}~dx\\=x\sin(\log x)-\int{\cos(\log x)}\\=x\sin(\log x)-I_1 \rightarrow(1)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-2dd56116322ffd1857ebbaf90c9ddda4_l3.png)
![Rendered by QuickLaTeX.com I_1\\= \displaystyle\int{\cos(\log x)}~dx\\=\cos(\log x)\int{dx}-\int{\left[\frac{d}{dx}(\cos(\log x)) \int{1 \cdot}~dx\right]}~dx\\=x\cos(\log x)+\int{\sin(\log x) \cdot \frac 1x \cdot x~dx}\\=x\cos(\log x)+\int{\sin(\log x)}~dx\\=x\cos(\log x)+I+c' \rightarrow(2)](https://examhoop.com/wp-content/ql-cache/quicklatex.com-c9ca458a69f959dc0382e04064d0c2e9_l3.png)
Hence, by ![]() we get,
we get,
![Rendered by QuickLaTeX.com I=x\sin(\log x)-(x\cos(\log x)+I+c') \\ \therefore I+I=x\sin(\log x) -x\cos(\log x) -c' \\ \text{or,}~~ 2I=x[\sin(\log x)-\cos(\log x)] -c' \\ \text{or,}~~ I=\frac x2[\sin(\log x)-\cos(\log x)]+c. ~~[~c=-c'/2~]](https://examhoop.com/wp-content/ql-cache/quicklatex.com-3988602cf77905fc6901813b18d05589_l3.png)
![]() Evaluate
Evaluate ![]() and
and ![]() by integrating each of them only once by parts.
by integrating each of them only once by parts.
Solution.


![]() Prove that,
Prove that, ![]()
Solution.
![Rendered by QuickLaTeX.com ~\displaystyle\int{\frac{e^x}{x^4}}~dx\\=e^x \int{\frac{1}{x^4}}~dx-\int{\left[\frac{d}{dx}(e^x) \int{\frac{1}{x^4}}~dx\right]}~dx\\=e^x \cdot \frac{x^{-4+1}}{-4+1}-\int{e^x \cdot \left(\frac{x^{-4+1}}{-4+1}\right)}~dx\\=\frac{e^x}{-3x^3}+\frac 13 \int{\frac{e^x}{x^3}}~dx\\=\frac{e^x}{-3x^3}+\frac 13\left[e^x\int{\frac{1}{x^3}}~dx- \int{e^x \left(-\frac{1}{2x^2}\right)}~dx\right]\\=\frac{e^x}{-3x^3}+\frac{e^x}{3} \cdot \frac{x^{-3+1}}{-3+1}+\frac 13 \cdot \frac 12 \int{\frac{e^x}{x^2}}~dx\\=\frac{e^x}{-3x^3}-\frac{e^x}{6x^2}+\frac 16 \left[e^x\int{\frac{1}{x^2}}~dx- \int{\left[\frac{d}{dx}(e^x) \int{x^{-2}}~dx\right]}~dx\right]\\=\frac{e^x}{-3x^3}-\frac{e^x}{6x^2}+\frac{e^x}{6} \cdot \left(\frac{x^{-2+1}}{-2+1}\right)-\frac 16\int{e^x \cdot \left(\frac{x^{-2+1}}{-2+1}\right)}~dx\\=\frac{e^x}{-3x^3}-\frac{e^x}{6x^2}-\frac{e^x}{6x}+\frac 16 \int{\frac{e^x}{x}}~dx\\=-\frac{e^x}{3}\left[\frac{1}{x^3}+\frac{1}{2x^2}+\frac{1}{2x}\right]+\frac 16 \int{\frac{e^x}{x}}~dx](https://examhoop.com/wp-content/ql-cache/quicklatex.com-51da439214fbc4be5f98a8d29cfee134_l3.png)