Straight Line | Part-1 |Ex-2A Examhoop

In the previous article, we completed Circle Chapter of Chhaya Mathematics, Class 11. In this article, we have solved 9 short answer type questions of Straight Line Chapter.

1.Find the equation of the straight line passing through the points $~(3,-4)~$ and $~(1,2)~$ and hence, show that the three points $~(3,-4),~(1,2)~$ and $~(2,-1)~$ are collinear.

Solution.

We know that the equation of the straight line in two-point form is $~\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\rightarrow(1)~,$ where $~(x_1,y_1)~$ and $~(x_2,y_2)~$ are two given points on the line.

So, using $~(1),~$ we get the straight line passing through the points $~(3,-4)~$ and $~(1,2)~$ which is

$\frac{y-(-4)}{x-3}=\frac{-4-2}{3-1} \\ \text{or,}~~ \frac{y+4}{x-3}=\frac{-6}{2} \\ \text{or,}~~ y+4=-3(x-3) \\ \text{or,}~~ y+4=-3x+9 \\ \text{or,}~~ 3x+y=5 \rightarrow(2)$

Hence , $~(2)~$ represents the equation of the straight line passing through the points $~(3,-4)~$ and $~(1,2)~$ .

2nd Part :

Clearly, the points $~(3,-4)~$ and $~(1,2)~$ lie on the straight line $~(2).$ Now, we put $~x=2,~y=-1~$ in $~(2)~$ so that

$~3 \times 2+(-1)=6-1=5~$ and so the point $~(2,-1)~$ lies on the straight line $~(2)~$ and so, we can conclude that the three points $~(3,-4),~(1,2)~$ and $~(2,-1)~$ are collinear.

2. The vertices of a triangle are $~(2,-2),~(4,2)~$ and $~(-1,3)~.$ Find the equation of the median through $~(-1,3).$

Solution.

Let the triangle be denoted by $~\Delta ABC~$ where $~A \equiv(-1,3),~B\equiv(4,2),~C(2,-2)~$ . So, the co-ordinates of the midpoint of the side $~BC~$ are $~D \equiv \left(\frac{4+2}{2},\frac{2-2}{2}\right)=(3,0).$

Now, the median through $~(-1,3)~$ must pass through the point $~D(3,0)~$ and so, the equation of $~AD~$ is

$y-3=\frac{0-3}{3+1} (x+1) \\ \text{or,}~~ 4(y-3)=-3(x+1) \\ \text{or,}~~3x+4y=12-3 \\ \therefore~~ 3x+4y=9.$

3. Find the equation of the straight line passing through the origin and dividing the segment of the straight line joining $~(4,-2)~$ and $~(1,10)~$ internally in the ratio $~2:1.$

Solution.

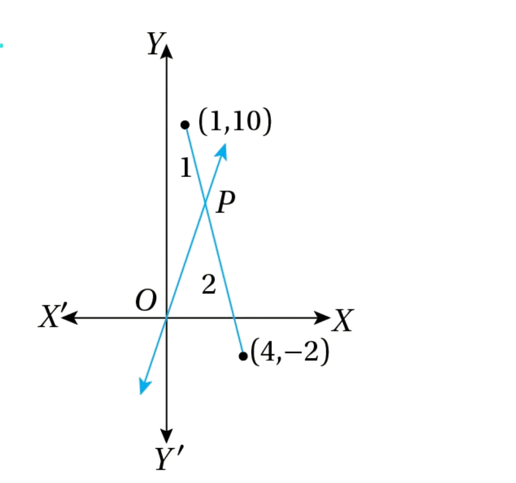
Suppose that the point $~P(x,y)~$ divides the straight line joining $~(4,-2)~$ and $~(1,10)~$ internally in the ratio $~2:1.$

$\text{So,}~ (x,y)=\left(\frac{2 \times 1+1 \times 4}{2+1},\frac{2 \times 10+1 \times (-2)}{2+1}\right)=\left(\frac{2+4}{3},\frac{20-2}{3}\right)=(2,6)$

Now, the equation of the straight line passing through $~(0,0)~$ and $~(2,6)~$ is

$\frac{y-0}{x-0}=\frac{0-6}{0-2} \\ \text{or,}~~ \frac{y}{x}=3 \\ \text{or,}~~ 3x-y=0.$

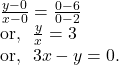
Hence, the equation of the straight line passing through the origin and dividing the segment of the straight line joining $~(4,-2)~$ and $~(1,10)~$ internally in the ratio $~2:1~$ is $~ 3x-y=0.$

4. A straight line passing through the point $~(3,5)~$ and is such that the portion of it intercepted between the axes is bisected at the point. Find the equation of the straight line and also its distance from the origin.

Solution.

Let the equation of straight line $~(AB)~$ be $~~\frac xa+\frac yb=1.$

$\therefore~$ the straight line intersects at $~x-$ axis and $~y-$ axis at $~A(a,0)~$ and $~B(0,b)~$ respectively.

So, the midpoint of $~AB~$ is $~\left(\frac a2,\frac b2\right).$

Now, according to the problem,

$(a/2, b/2)=(3,5) \\ \therefore \frac a2=3 \Rightarrow a=6, ~~ \frac b2=5 \Rightarrow b=10.$

$\therefore~$ the equation of the straight line :

$\frac x6+\frac{y}{10}=1 \\ \text{or,}~~ \frac{5x+3y}{30}=1 \\ \text{or,}~~ 5x+3y-30=0 \rightarrow(1)$

So, distance of the straight line $~(1)~$ from the origin is

$\left|\frac{5 \times 0+3 \times 0-30}{\sqrt{5^2+3^2}}\right|=\frac{30}{\sqrt{34}}~~\text{unit}.$

5. A straight line passes through the point $~(1,2)~$ and is such that the portion of it intercepted between the axes is divided internally at the point in the ratio $~3:2.~$ Find the equation of the line.

Solution.

Let the equation of straight line $~(AB)~$ be $~~\frac xa+\frac yb=1.$

$\therefore~$ the straight line intersects at $~x-$ axis and $~y-$ axis at $~A(a,0)~$ and $~B(0,b)~$ respectively.

Suppose that the point $~P(x,y)~$ divides the straight line joining $~(a,0)~$ and $~(0,b)~$ internally in the ratio $~3:2.$

$\therefore (x,y)=\left(\frac{3 \times 0+2a}{3+2},\frac{3b+2 \times 0}{3+2}\right)=\left(\frac{2a}{5},\frac{3b}{5}\right).$

So, according to the problem,

$\left(\frac{2a}{5},\frac{3b}{5}\right)=(1,2) \\ \therefore~ \frac{2a}{5}=1 \Rightarrow a=\frac 52,~~\frac{3b}{5}=2 \Rightarrow b=\frac{10}{3}.$

$\therefore~$ the equation of the straight line

$\frac{x}{5/2}+\frac{y}{10/3}=1 \\ \text{or,}~~ \frac{2x}{5}+\frac{3y}{10}=1 \\ \text{or,}~~ 4x+3y=10.$

6. Find the locus of the middle point of the portion of the line-segment made by the straight line $~x\cos\alpha+y\sin\alpha=4~$ and the axes of co-ordinates.

Solution.

We have the given equation of straight line $~(AB)~$ as follows :

$~x\cos\alpha+y\sin\alpha=4 \\ \text{or,}~~ \frac{x}{(4/\cos\alpha)}+\frac{y}{(4/\sin\alpha)}=1$

$\therefore~$ the straight line intersects at $~x-$ axis and $~y-$ axis at $~A\left(\frac{4}{\cos\alpha},0\right)~$ and $~B\left(0,\frac{4}{\sin\alpha}\right)~$ respectively.

Let $~(h,k)~$ be the co-ordinates of the midpoint $~AB.$

$\therefore~ h=\frac 12\left(\frac{4}{\cos\alpha}+0\right),~~k=\frac{1}{2}\left(0+\frac{4}{\sin\alpha}\right) \\~~ \text{or,}~~ h=\frac{2}{\cos\alpha}, ~~ k=\frac{2}{\sin\alpha} ; \\ ~~ \text{or,}~~ \cos\alpha=\frac 2h, ~~ \sin\alpha=\frac 2k.$

$\text{Now,}~~ \sin^2\alpha+\cos^2\alpha=1 \\~~~ \text{or,}~~(2/k)^2+(2/h)^2=1 \\ ~~~\text{or,}~~\frac{4}{k^2}+\frac{4}{h^2}=1 \\~~~ \text{or,}~~ \frac{1}{h^2}+\frac{1}{k^2}=\frac 14 \rightarrow(1)$

Hence, by $~(1),~$ we can conclude that the locus of the middle point of the portion of the line-segment made by the straight line is $~ \frac{1}{x^2}+\frac{1}{y^2}=\frac 14.$

7. A straight line moves in such a manner that the sum of the reciprocals of its intercepts upon the axes is always constant. Show that the line passes through a fixed a point.

Solution.

Suppose that the straight line cuts the $~x-$ axis and $~y-$ axis at $~A(a,0)~$ and $~B(0,b)~$ respectively.

So, the equation of the straight line is $~\frac xa+\frac yb=1 \rightarrow(1)$

According to the problem,

$~\frac 1a+\frac 1b=k~~\text{(constant)} \\ \text{or,}~~ \frac{1/k}{a}+\frac{1/k}{b}=1 \rightarrow(2)$

Now, comparing $~(1)~$ and $~(2)~$ we conclude that the straight line $~(1)~$ always passes through the point $~\left(\frac 1k,\frac 1k\right).$

8. The numerical value of the area of the triangle formed by a moving line on the co-ordinate axes is $~2c^2.~$ Find the locus of the middle point of the portion of the line intercepted between the axes.