Ellipse (S.N.Dey)|Part-5|Ex-5 Examhoop

In the previous article , we solved 7 solutions of Short Answer Type Questions (from 8-14) of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.

15. If $~t~$ be a variable parameter, show that the point $~x=a~\frac{1-t^2}{1+t^2},~y=b~\frac{2t}{1+t^2}~$ always lies on an ellipse.

Solution.

$x=a\frac{1-t^2}{1+t^2}\rightarrow(1),~y=b\frac{2t}{1+t^2}\rightarrow(2)$

From $~(1)~$ and $~(2)~$ we get,

$\left(\frac xa\right)^2+\left(\frac yb\right)^2\\=\frac{(1-t^2)^2+(2t)^2}{(1+t^2)^2}\\=\frac{(1-t^2)^2+4t^2}{(1+t^2)^2}\\=\frac{(1+t^2)^2}{(1+t^2)^2}\\=1 \\ \therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\rightarrow(1)$

Clearly, equation $(1)$ represents an ellipse. Hence, the point always lies on an ellipse.

16. A point moves on a plane in such a manner that the sum of its distances from the points $~(5,0)~$ and $~(-5,0)~$ is always constant and equal to $~26.~$ Show that the locus of the moving point is the ellipse $~\frac{x^2}{169}+\frac{y^2}{144}=1.$

Solution.

Let the co-ordinates of the moving point be $P(h,k).$ Also, let $~S \equiv (5,0),~~S' \equiv (-5,0).$

$\therefore~ PS+PS'=26 \\ \text{or,}~~ \sqrt{(h-5)^2+k^2}+\sqrt{(h+5)^2+k^2}=26 \\ \text{or,}~~ \sqrt{(h-5)^2+k^2}=26-\sqrt{(h+5)^2+k^2} \\ \text{or,}~~ (h-5)^2+k^2=26^2+(h+5)^2+k^2-2 \times 26 \sqrt{(h+5)^2+k^2} \\ \text{or,}~~ 2 \times 26 \sqrt{{(h+5)^2+k^2}}=(h+5)^2-(h-5)^2+26^2 \\ \text{or,}~~ 2 \times 26 \sqrt{(h+5)^2+k^2}=(h+5+h-5)(h+5-h+5)+26^2 \\ \text{or,}~~ 2 \times 26 \sqrt{(h+5)^2+k^2}=2h \times 10+26^2 \\ \text{or,}~~ 26\sqrt{(h+5)^2+k^2}=10h+26\times 13 \\ \text{or,}~~ 13\sqrt{(h+5)^2+k^2}=5h+13^2 \\ \text{or,}~~ \sqrt{(h+5)^2+k^2}=\frac{5}{13}h+13 \\ \text{or,}~ (h+5)^2+k^2=\left(\frac{5}{13}h\right)^2+2 \cdot \frac{5}{13}h \cdot 13+13^2 \\ \text{or,}~~ h^2+10h+25+k^2=\left(\frac{5}{13}\right)^2h^2+10h+13^2 \\ \text{or,}~~ h^2\left(1-\frac{5^2}{13^2}\right)+k^2=13^2-25 \\ \text{or,}~~ h^2 \times \frac{12^2}{13^2}+k^2=144=12^2 \\ \text{or,}~~ \frac{h^2}{13^2}+\frac{k^2}{12^2}=1 \\ \therefore \frac{h^2}{169}+\frac{k^2}{144}=1\rightarrow(1)$

Hence, by $~(1)~$ we can conclude that the locus of moving point $~\frac{x^2}{169}+\frac{y^2}{144}=1~$ which represents an ellipse.

17. Find the locus of the point , the ratio of whose distances from the line $~x-8=0~$ and from the point $~(2,0)~$ is $~2:1.$

Solution.

Let the co-ordinates of the point $(P)$ be $~(h,k).$

The distance $(s)$ of P from the line $~x-8=0~$ is

$~s=\frac{|h-8|}{\sqrt{1^2}}=|h-8|.$

Again, the distance $(d)$ of P from the point $~(2,0)~$ is

$~d=\sqrt{(h-2)^2+(k-0)^2}=\sqrt{(h-2)^2+k^2}$ .

By question,

$\frac sd=2 \\ \text{or,}~~ s=2d \\ \text{or,}~~ s^2=4d^2 \\ \text{or,}~~ (h-8)^2=4[(h-2)^2+k^2] \\ \text{or,}~~ h^2-16h+64=4(h^2-4h+4+k^2) \\ \text{or,}~~ 64-16=4h^2-16h+4k^2+16h-h^2 \\ \text{or,}~~ 3h^2+4k^2=48.$

Hence, the locus of the point is $~3x^2+4y^2=48.$

18. The lengths of the major and minor axes of an ellipse are $~2a~$ and $~2b~$ and $~N~$ is the foot of the perpendicular drawn from a point $~P~$ of the ellipse on the major axis. Show that, $~\frac{PN^2}{\overline{AN} \cdot \overline{A'N}}=\frac{b^2}{a^2}~$ where $~A~$ and $~A'~$ are the two vertices of the ellipse.

Solution.

The equation of the ellipse is $~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\rightarrow(1).$

Let the co-ordinates of P be $~(h,k).$

The co-ordinates of the foot of the perpendicular drawn from $~P(h,k)~$ on the major axis at $~N(h,0).$

$\therefore~\overline{PN}=|k|$

$\because~~A~$ and $~A'~$ are the vertices of the ellipse,

$\therefore~ \overline{AN}=|h+a|~$ and $~\overline{A'N}=|h-a|.$

$\frac{PN^2}{\overline{AN}\cdot \overline{A'N}}=\frac{|k|^2}{|h+a||h-a|}=\frac{k^2}{|(h+a)(h-a)|}=\frac{k^2}{|h^2-a^2|}=\frac{k^2}{a^2-h^2}(\because~ a \geq h)\rightarrow(2)$

Since the point $~P(h,k)~$ lies on the ellipse $(1)$

$\frac{h^2}{a^2}+\frac{k^2}{b^2}=1 \\ \therefore \frac{k^2}{b^2}=1-\frac{h^2}{a^2}=\frac{a^2-h^2}{a^2} \\ \text{or,}~~ \frac{k^2}{a^2-h^2}=\frac{b^2}{a^2}\rightarrow(3)$

Hence, by $(2)$ and $(3)$ , we get

$\frac{PN^2}{\overline{AN}\cdot \overline{A'N}}=\frac{b^2}{a^2}~~\text{(showed)}$

19. Show that for an ellipse the straight line joining the upper end of one latus rectum passes through the centre of the ellipse.

Solution.

Let the equation of the ellipse be $~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1~~(a^2>b^2)\rightarrow(1)$

The co-ordinates of foci of the ellipse $(1)$ is $~(\pm ae,0).$

Now, the co-ordinates of the upper end of latus rectum passing through the focus $(ae,0)$ is $~L\left(ae,\frac{b^2}{a}\right).$

Again, the co-ordinates of the lower end of latus rectum passing through the focus $(-ae,0)$ is $~L'\left(-ae,-\frac{b^2}{a}\right).$

So, the mid-point of $LL'$ is $~\left(\frac{1}{2}(ae-ae),\frac12(\frac{b^2}{a}-\frac{b^2}{a})\right)=(0,0).$

Hence, $~LL'~$ passes through the centre of the ellipse.

$20.~$ Find the equation of the auxiliary circle of the ellipse $~16x^2+25y^2+32x-100y=284.$

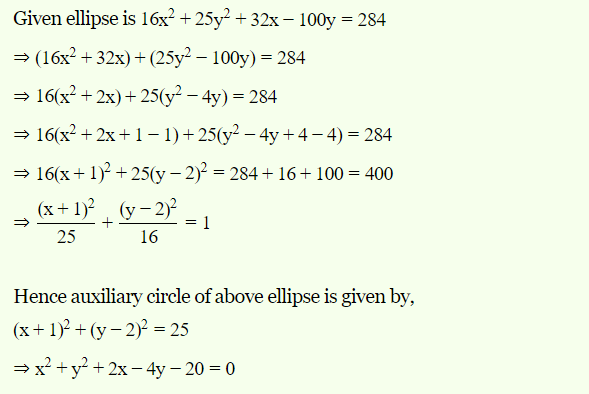
21. If the eccentric angles of the two points on the ellipse $~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1~(a^2>b^2)~$ are $~\theta_1~$ and $~\theta_2~$ then prove that the equation of the chord passing through these two points is $~\frac xa \cos \frac{\theta_1+\theta_2}{2}+\frac yb \sin\frac{\theta_1+\theta_2}{2}=\cos\frac{\theta_1-\theta_2}{2}.$

Solution.

By question, let $~P(a\cos\theta_1,b\sin\theta_1)~$ and $~P'(a\cos\theta_2,b\sin\theta_2)~$ be two points on the given ellipse $~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \rightarrow(1)$

Now, the equation of the chord $PP'$ of $(1)$ is

$y-b\sin\theta_1=\frac{b(\sin\theta_2-\sin\theta_1)}{a(\cos\theta_2-\cos\theta_1)}(x-a\cos\theta_1) \\ \text{or,}~~ y-b\sin\theta_1\\=\frac ba \cdot \frac{-2\cos\left(\frac{\theta_1+\theta_2}{2}\right)\sin\left(\frac{\theta_1-\theta_2}{2}\right)}{2\sin\left(\frac{\theta_1+\theta_2}{2}\right)\sin\left(\frac{\theta_1-\theta_2}{2}\right)}(x-a\cos\theta_1)\\=-\frac ba \cdot \frac{\cos\left(\frac{\theta_1+\theta_2}{2}\right)}{\sin\left(\frac{\theta_1+\theta_2}{2}\right)}(x-a\cos\theta_1) \\ \therefore \frac yb \sin\left(\frac{\theta_1+\theta_2}{2}\right)-\sin\theta_1 \cdot \sin\left(\frac{\theta_1+\theta_2}{2}\right)\\=-\frac xa\cos\left(\frac{\theta_1+\theta_2}{2}\right)+\cos\theta_1 \cos\left(\frac{\theta_1+\theta_2}{2}\right) \\ \text{or,}~~ \frac xa \cos \left(\frac{\theta_1+\theta_2}{2}\right)+\frac yb\sin\left(\frac{\theta_1+\theta_2}{2}\right)=\cos\theta_1 \cos\left(\frac{\theta_1+\theta_2}{2}\right)+\sin\theta_1\sin\left(\frac{\theta_1+\theta_2}{2}\right)\\=\cos\left(\theta_1-\frac{\theta_1+\theta_2}{2}\right)=\cos\left(\frac{\theta_1-\theta_2}{2}\right).$

22. If the eccentric angles of the extremities of two chords which are passing through two points on major axis and the points are equidistant from centre of the ellipse, are $~\alpha, \beta, \gamma,\delta~$ respectively, then show that $~\tan\alpha \tan\beta \tan\gamma\tan\delta=1.$

Solution.

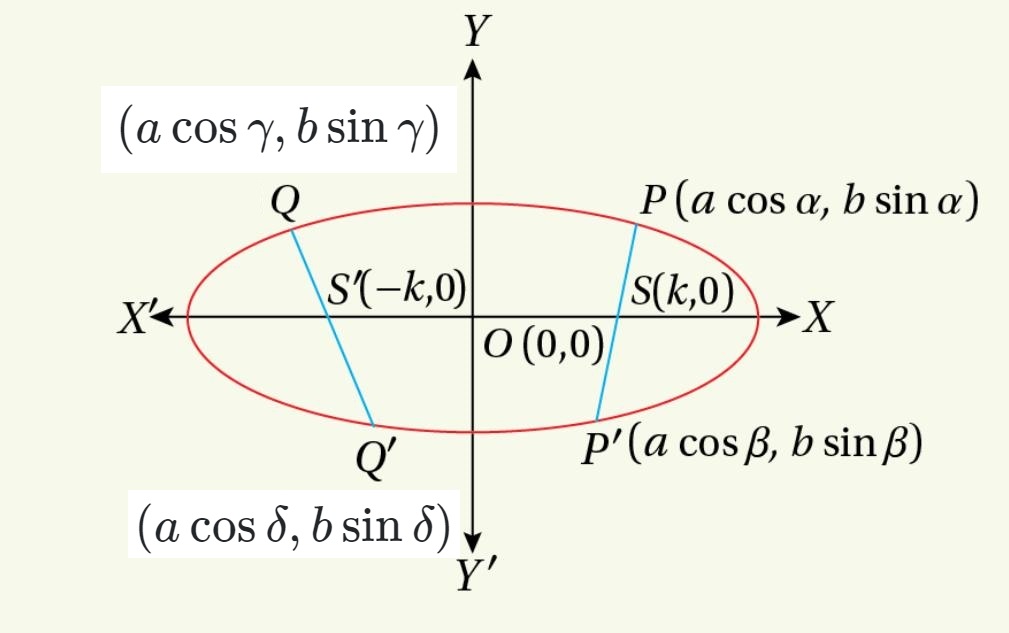
Let the equation of the ellipse be $~\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$

Also, suppose that $PP'$ and $QQ'$ are two chords of the ellipse whoch are equidistant from the centre of the ellipse. Consider that two chords intersect the major axis at $~S(k,0)$ and $S'(-k,0)$ respectively.

Let the eccentric angles of the points $~P,P',Q,Q'~$ be $~\alpha,\beta,\gamma,\delta~$ respectively.

$\therefore~ P\equiv (a\cos\alpha,b\sin\alpha),~~P' \equiv(a\cos\beta,b\sin\beta),\\~~~Q \equiv (a\cos\gamma,b\sin\gamma),Q'\equiv (a\cos\delta,b\sin\delta).$

Now, the slope of $~SP'=~$ the slope of $~~SP$

$\\ \text{or,}~~ ~\frac{0-b\sin\beta}{k-a \cos \beta}=\frac{0-b\sin\alpha}{k-a\cos\alpha} \\ \text{or,}~~ \frac{\sin\beta}{k-a\cos\beta}=\frac{\sin\alpha}{k-a\cos\alpha} \\ \text{or,}~~ k\sin\alpha- a\cos\beta\sin\alpha=k\sin\beta-a\cos\alpha\sin\beta\\ \text{or,}~~ k(\sin\alpha-\sin\beta)=a(\sin\alpha\cos\beta-\cos\alpha\sin\beta) \\ \text{or,}~~ \frac ka=\frac{\sin(\alpha-\beta)}{\sin\alpha-\sin\beta}=\frac{-\sin(\beta-\alpha)}{-(\sin\beta-\sin\alpha)} \\ \text{or,}~~ \frac ka=\frac{2\sin\left(\frac{\beta-\alpha}{2}\right)\cos\left(\frac{\beta-\alpha}{2}\right)}{2\sin\left(\frac{\beta-\alpha}{2}\right)\cos\left(\frac{\beta+\alpha}{2}\right)}=\frac{\cos\left(\frac{\beta-\alpha}{2}\right)}{\cos\left(\frac{\beta+\alpha}{2}\right)} \\ \text{or,}~~ \frac{k+a}{k-a}=\frac{\cos\left(\frac{\beta-\alpha}{2}\right)+\cos\left(\frac{\beta+\alpha}{2}\right)}{\cos\left(\frac{\beta-\alpha}{2}\right)-\cos\left(\frac{\beta+\alpha}{2}\right)} \\ \therefore \frac{k+a}{k-a}=\frac{2\cos(\alpha/2)\cos(\beta/2)}{2\sin(\alpha/2)\sin(\beta/2)}=\cot(\alpha/2)\cot(\beta/2)\rightarrow(1)$

Similarly, the slope of $~S'Q'=~$ the slope of $~S'Q$

$\text{or,}~~ \frac{0-b\sin\delta}{-k-a\cos\delta}=\frac{0-b\sin\gamma}{-k-a\cos\gamma} \\ \text{or,}~~ \frac{\sin\delta}{k+a\cos\delta}=\frac{\sin\gamma}{k+a\cos\gamma} \\ \text{or,}~~ k\sin\gamma+a\cos\delta\sin\gamma=k\sin\delta+a\cos\gamma\sin\delta \\ \text{or,}~~ a(\sin\gamma\cos\delta-\cos\gamma\sin\delta)=k(\sin\delta-\sin\gamma) \\ \text{or,}~~ a \sin(\gamma-\delta)=k(\sin\delta-\sin\gamma) \\ \text{or,}~~ \frac ka=\frac{\sin(\gamma-\delta)}{\sin\delta-\sin\gamma}=\frac{2\sin\left(\frac{\gamma-\delta}{2}\right)\cos\left(\frac{\gamma-\delta}{2}\right)}{-2\cos\left(\frac{\gamma+\delta}{2}\right)\sin\left(\frac{\gamma-\delta}{2}\right)} \\ \text{or,}~~ \frac ka=-\frac{\cos\left(\frac{\gamma-\delta}{2}\right)}{\cos\left(\frac{\gamma+\delta}{2}\right)} \\ \therefore ~\frac{k+a}{k-a}=\frac{\cos\left(\frac{\gamma+\delta}{2}\right)-\cos\left(\frac{\gamma-\delta}{2}\right)}{-\left[\cos\left(\frac{\gamma-\delta}{2}\right)+\cos\left(\frac{\gamma+\delta}{2}\right)\right]} \\ \text{or,}~~ \frac{k+a}{k-a}=\frac{-2\sin(\gamma/2)\sin(\delta/2)}{-2\cos(\gamma/2)\cos(\delta/2)}=\tan(\gamma/2)\tan(\delta/2)\rightarrow(2)$

Hence, from $(1)$ and $(2)$ we get,

$\cot(\alpha/2)\cot(\beta/2)=\tan(\gamma/2)\tan(\delta/2) \\ \text{or,}~~ \tan(\alpha/2)\tan(\beta/2)\tan(\gamma/2)\tan(\delta/2)=1~~\text{(proved)}$

Post Views: 247

In the previous article , we solved 7 solutions of Short Answer Type Questions (from 8-14) of Ellipse Chapter of S.N.Dey mathematics, Class 11. In this chapter, we will solve few more.

Leave a Comment Cancel reply